[CVPR 2018 oral] Context Encoding for Semantic Segmentation

[CVPR 2018 oral] Context Encoding for Semantic Segmentation

참고자료:

[0] 원논문 저자 사이트: https://hangzhang.org/PyTorch-Encoding/model_zoo/segmentation.html

[1] CVPR2018 Oral Presentation [CVPR18 Oral] Context Encoding for Semantic Segmentation (https://www.youtube.com/watch?v=vAhzirU4WqA)

[2] 동영상 https://paperswithcode.com/paper/location-aware-upsampling-for-semantic/review/

Code 자료:

[1] https://github.com/zhanghang1989/PyTorch-Encoding

Abstract

• 최근 Fully Convolutional Network framework로 Dilated/Atrous convolution, multi-scale features, 그리고 refining boundaries을 활용하여 pixel wise labeling spatial resolution을 개선한 연구들이 있었다.
• Context Encoding Module을 도입하여, global context information의 영향을 탐색하였다.
  • Context Encoding Module?: 이미지들의 semantic context를 잡아내고(capture), class-depdendent featuremaps를 통해 class를 선별적으로 강조하는 모듈.
• 간단한 Context Encoding Module을 도입하는 것으로, 10배 많은 layer를 가진 SOTA 모델과 비등한 성능을 이끌어냈다.

1. Introduction

• 정확한 모양과 경게선을 예측하는 어려움

• Per-pixel predictions of object categories
• A comprehension scene description (object category, location, and shape)
  • 하나의 scene에서 object categories, location and shape정보에 대한 총체적인 기술을 내포함시킴

• Q> 모델의 어떤 component에서 다음 comprehensive description을 이끌어냈는가?
  • object category : encoding layer in Context encoding module
  • location:
  • shape:
• Meta algorithm(?) for Semantic Segmentation
• Pre-trained CNN + Decoder
• Translation equivariant
  • (Equivariance란, 함수의 입력이 바뀌면 출력 또한 바뀐다는 뜻이고, translation equivariance는 입력의 위치가 변하면 출력도 동일하게 위치가 변한채로 나온다는 뜻이다.)

• Decoder (on top)는 downsampled featuremap의 디테일 성분들을 복원한다.

• Atrous Convolution? (a trous: 불어로, 구멍이 있는.)

  출처: https://better-tomorrow.tistory.com/entry/Atrous-Convolution

  1. 일반적인 convolution

  

  1. Atrous convolution(dilated convolution)

  

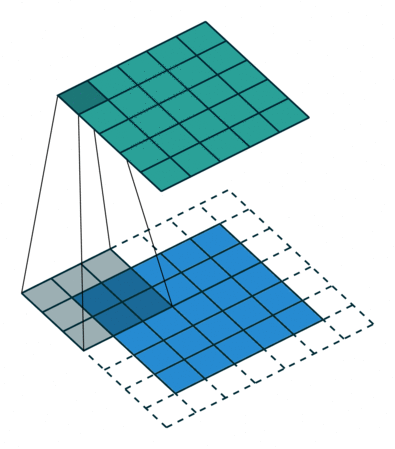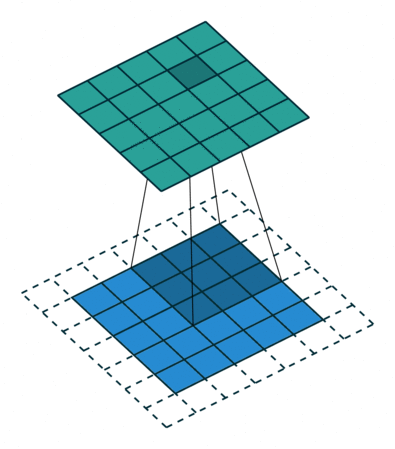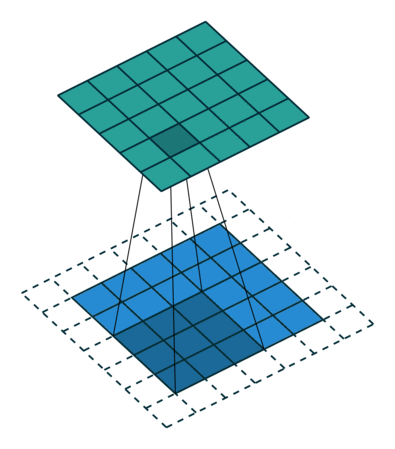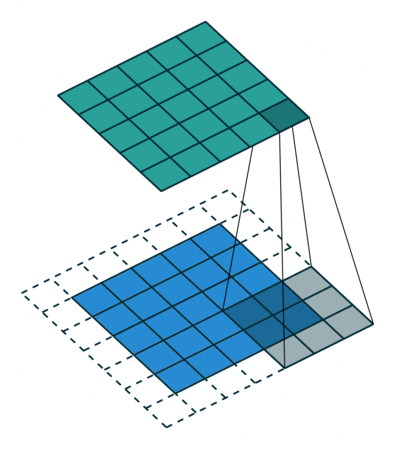
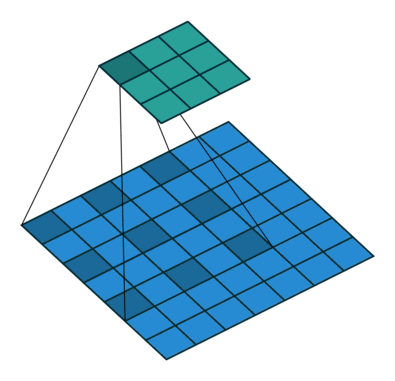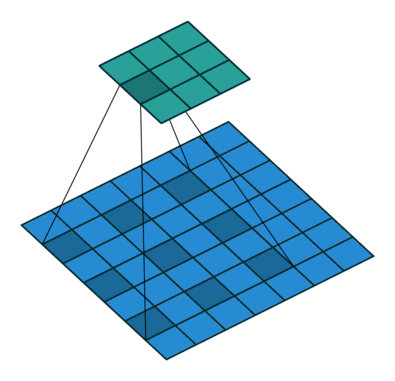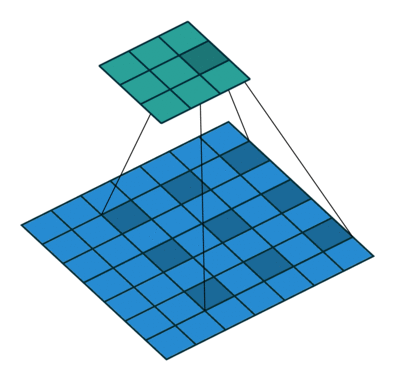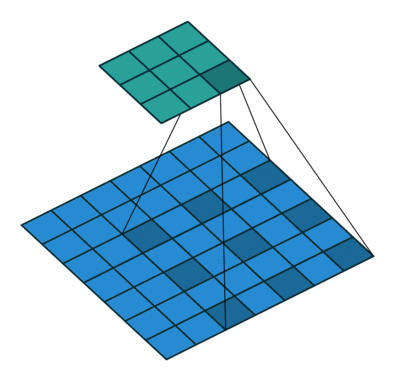
  출처 : https://towardsdatascience.com/types-of-convolutions-in-deep-learning-717013397f4d

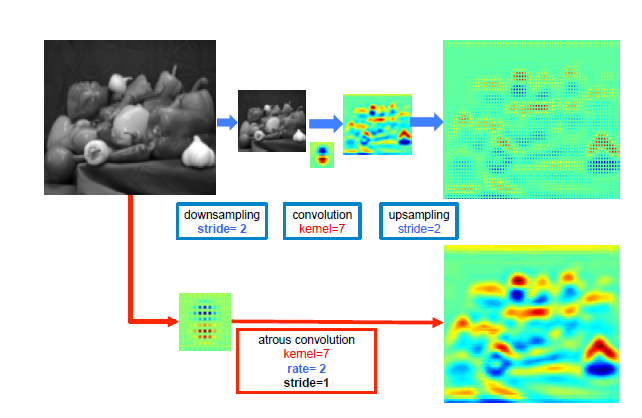
  위 두 이미지를 한 번 살펴보자

  일반적인 convolution과 달리 atrous convolution의 경우 kernel 사이가 한 칸씩 띄워져 있는 것을 확인할 수 있다.

  그렇다면 atrous는 무슨 의미일까?

  구글 검색기를 돌려보니 프랑스어로 a trous는 구멍이 있는 이라는 뜻이다.

  

  이 말은 kernel 사이에 구멍이 있는 convolution이라는 뜻으로 볼 수 있다.

  이런 kernel 사이의 간격을 dilation rate라고 정의하며 일반적인 convolution의 경우 dilation rate가 1로 볼 수 있다.

  그렇다면 위 atrous convolution 이미지의 dilation rate는 2라고 볼 수 있다.

  atrous convolution의 경우 중간 구멍을 0으로 채워지게 해서

  그렇다면 왜 이렇게 kernel 중간에 간격을 두는 것일까?

  그것은 일반적인 convolution와 동일한 computational cost로 더 넓은 field of view(큰 receptive field)를 제공하기 때문이다. 위 이미지와 비교해보면 일반적인 convolution의 receptive field는 3 x 3에 불과하지만 atrous convolution 경우 동일한 parameter로 5 x 5의 receptive field를 가져간다.

  아래 deeplabv2의 논문 이미지를 봐보자

  

  출처 : DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs

  윗 부분은 일반적인 convolution, 아래 부분은 atrous convolution을 적용하여 나온 feature map을 보여준다. 동일한 해상도에서, 일반적인 convolution을 보면 feature가 sparse하게 추출된 반면, atrous convolution의 경우 feature가 dense하게, 더 두드러지게 추출된 것을 확인할 수 있다.

  그렇다면 kernel 사이의 간격을 추가해 receptive field를 크게하는 이유는 무엇일까?

  일반적인 classification의 경우 detail한 정보보단 대상의 존재 여부만을 확인하는데 집중한다. 그렇기 때문에 convolution과 pooling을 조합하여 object의 변화에 큰 영향을 받지 않은 강인하고 축약된 정보만을 사용한다. 그래서 detail보다는 global information에 집중을 한다.

  반면 semantic segmentation의 경우 픽셀단위의 조밀한 예측(dense prediction)이 필요하다.

  classification network를 그대로 사용할 경우 계속 feature map의 크기가 줄어들기 때문에 detail한 정보를 얻는데 어려움이 있다.

  이를 해결하기 위해 deeplab에서는 pooling layer를 없애고, atrous convolution을 이용하여 receptive field를 확장시키는 효과를 얻었다.

  

kernel 사이에 구멍이 있는 convolution이라는 뜻으로 볼 수 있다.

이런 kernel 사이의 간격을 dilation rate라고 정의하며 일반적인 convolution의 경우 dilation rate가 1로 볼 수 있다.

Contribution 1

1. Context Encoding Module을 도입한 것. 그리고 여기에 Semantic Encoding Loss(SE-loss)를 같이 도입한 것.
   1. Context Encoding Module이라는 단순한 unit을 추가해줌으로써, Global scene context정보를 활용할 수 있다.
      • global context를 잡아내기 위해서, 그리고 class-dependent feature maps을 선별적으로 강조하기 위해, Encoding layer를 통합한다.
      • 네트워크가 해당 특정 scene안에서 어떤 물체가 존재하는 지를 예측하여, → semantics context에 대한 학습을 하도록 유도(enforce)한다.
      • 가령, 실내 이미지에서는 자동차의 가능성을 강조하지 않고(de-emphasized), city space 이미지에서는 도로(건물)와 비행기 보다는 도로(건물)와 자동차가 동시에 출연할 가능성이 높으므로 자동차의 가능성을 강조한다. (CVPR oral 내용)

   b. SE-loss: per-pixel loss와 다르게, SE-loss는 [ 크고 작은 objects들에 대해서 동일한 Contribution를 매김으로써, ] 측면에서 training 을 regularizing한다.

   • 표준이 되는 기존의 훈련 방식(standard training process)은 오직 per-pixel segmentation loss를 사용하였고, 특정 input scene에서 global context를 강하게 사용하지 않고 있었다.

⇒ 결론적으로 단순한 구조이면서도, FCN based approach와 비등한(compatible) 성능을 보인다.

Contribution 2

1. 새로운 Semantic Segmentation framework인 Context Encoding Network의 design과 구현
   • Context encoding module을 포함시켜서, pre-trained Deep Residual Networ (ResNet)을 증강할 수 있다.

   • pre-trained Network에 Dilation strategy를 사용하였다.

   • EncNet은 85.9% mIoU PASCAL VOC 2012 and 51.7% on PASCAL in Context 의 성능을 보였다.
   • 우리의 EncNet-101(ResNet101 backbone) single 모델은 55.67% 의 성능을 보였다.

   • 오직 3.5M 파라미터들로 3.96%의 error rate를 달성했다.

   • 추가적으로 synchronized multi-GPU Batch Normalization을 구현하여 도입했고, Memory효율적인 Encoding layer를 구현했다.

2. Context Encoding Module

• Contextual information을 이해하고 활용하는 것이 semantic segmentation에서 중요하다.
  • Q> Contextual information?

  

Context Encoding

• 피쳐 통계량을 잡아내기 위해 Encoding Layer를 사용했다.
• encoded context (encoded semantcis): C x 1 x 1

  • 

• The encoder dramatically reduce the search space!

• Global context information can be encoded using a video encoder such as bag of words,
• Deep learning encoding process is still counted and as powerful
• encoding layer which integrateds the entire dictionary learning and residual encoding into a single CNN layer can be learned from end2end.

• including layer to capture the feature statistics as a global semantic context
  • consider a set of channel dimensional features
  • learns a code book and smoothing factors directly from loss functions using stochastic gradient descent
    • and it outputs to residual encoders by s

• codebook D? : Scene에서 나올 수 있는 class categories를 모두 모아 놓은, 일종의 Dictionary같은 존재.
• smoothing factors S의 역할?
  • 뇌피셜: ` 첫번째의 layer가 각 cluster 별로 다르게 텐서가 뽑히는 것을 normalize해주기 위함이 아닐까?`
    • check!

• Code Book : DeepTen

  출처: https://vision4me.tistory.com/2

  시작에 앞서 잠깐 TMI를 드리자면, 2017 CVPR에 Deep TEN과 함께 소개되었던 DAIN(Differential Angular Imaging Network)과 더불어 모두 같은 연구실에서 나온 논문입니다. 미국 Rutgers 대학의 Kristin Dana 교수 산하 연구실인데 최근 좋은 성능을 보이는 재질 인식 논문들은 거의 모두 여기서 나왔다고 해도 무방합니다.

  ### Deep TEN - Base Idea

  먼저 객체 인식과 비교할 때 재질 인식이 가지는 가장 큰 특징이 무엇일지 생각해보는 걸로 시작하겠습니다.

  일반적인 객체 인식에서 shape, spatial arrangement와 같은 정보가 주요한 feature로서 작용하는 것과는 달리, 객체 인식은 반대로 shape-invariant한 정보를 추출하는 데에 목적을 둡니다. 논문에서도 scene understanding, object recognition 등의 task와 비교해 texture recognition이 가지는 차이점을 언급하고 있습니다.

  의자(혹은 의자의 재질)을 인식하는 경우를 생각해 보겠습니다. 기존 객체 인식 목적의 deep learning network가 하는 일은 추출된 각 local feature 같의 spatial arrangement를 보존하면서 이 상대적인 연관관계를 통해 의자의 외형을 특정짓는 일입니다. 하지만 재질인식에서 이와 같은 방식을 사용하게 되면, 의자의 외형에 dependent한 feature가 추출되기 때문에, 좋은 재질 feature라고 볼 수 없겠죠.

  그래서 이 논문은 재질을 특정지을 수 있는 spatially-invariant, order-less한 feature의 필요성을 주장합니다. 그렇다면 어떻게 그런 feature를 얻느냐. Deep TEN은 기존 dictionary learning / feature distribution 에서 그 해답을 찾았습니다.

  ### BoW(Bag of Words) 기법

  논문을 좀 더 잘 이해하기 위해, 잠시 기반 지식을 짚고 넘어가겠습니다. BoW 기법은 이름에서 추측할 수 있듯이, 특정 단어(word)들의 조합과 갯수로 대상을 특정짓는 기법입니다. 기존에는 문서 분류 분야에서 많이 사용되었는데요, 예를 들어 특정 논문을 읽는다고 할 때 ‘texture’, ‘material’, ‘surface’ 같은 단어가 많이 발견된다면 이 논문은 ‘재질’에 관련된 문서일 확률이 높아지겠죠. 이미지 인식에 적용되어도 얘기는 크게 다르지 않습니다.

  시작은 우선 복수의 대상 객체(이미지)로부터 feature 를 추출하는 것으로 시작합니다. 기존에 제시되었던 여러 feature extraction 기법들을 이용해 feature를 추출하고, 추출된 feature들에 clustering을 적용합니다. 생성된 각각의 cluster는 해당 cluster를 정의하는데 핵심적인, cluster의 center에 위치하는 대표 feature들을 갖게 됩니다. 이 대표 feature들이 바로 code book(dictionary)를 구성하는 ‘code’가 됩니다.  이 때, ‘몇 개의 cluster’로 feature space를 정의하는지에 따라 code book을 구성하는 code의 갯수도 달라지겠죠. 만일 적은 수의 code로 space를 정의한다면 아주 significant한 몇 개의 feature를 바탕으로 classification을 수행할 것이고, 많은 수의 code로 space를 정의한다면 좀 더 복잡하되 서로 구분이 명확하지 않은 복수의 feature로 classification을 수행하게 될 것 입니다.

  이제 새로운 이미지 A가 들어왔다고 가정해보겠습니다. code book을 생성할 때 적용했던 feature extraction 기법들을 동일하게 적용하고 나면, 이미지 A에 해당하는 복수의 feature들이 추출되었을 것입니다. 이제 이 feature들을 기존 code 들이 정의된 feature space상에 대입해, 좀 더 가까운 (비슷한 값을 가지는) code 들이 무엇인지를 파악하게 됩니다. 이렇게 이 이미지 A가 가지고 있다고 판단되는 코드들을 파악해, 이 코드들의 distribution(histogram)을 만들어 classification을 수행하는 게 바로 image classification에서 사용되는 dictionary 기반 학습 기법입니다.

  이 기법은 Deep TEN 논문이 주장한대로 (code 의 갯수로 distribution을 생성하기 때문에) order-less, spatially-variant 한 feature를 추출할 수 있다는 장점이 있지만, 반대로 feature 들 간의 spatial arrangement 정보를 잃어버린다는 단점이 있습니다. 이 부분에 대해서는 두 번째 논문 (Deep Texture Manifold)에서 다루고 있으니 다음 포스트에서 좀 더 자세히 설명하겠습니다.

  참조: https://darkpgmr.tistory.com/125

  ### Residual Encoding Model

  다시 Deep TEN으로 돌아오겠습니다.

  위에 설명한 것과 같은 dictionary learning 기반 방식을 재질 인식에 적용하려는 시도는 이전에도 있었습니다. 가장 잘 알려진 예가 2015년 CVPR에서 발표된 Deep filter bank 방법인데요, 해당 논문은 기존에 사용되었던 여러 feature extraction 방식(SIFT 등)과 encoder(VLAD, Fisher Vector)들을 혼합해 발표 당시 몇 가 재질 데이터셋에 대해 state-of-the-art를 기록했습니다.  하지만 이 논문은 여전히 아래와 같은 두 가지 한계점을 가진다는 것이 Deep TEN의 지적입니다.

  • pre-trained CNN, dictionary learning, encoding 등 별도의 알고리즘 component들이 각자 생성된 뒤 합쳐지는 형식을 가지고 있음 (즉, end-to-end가 아님)
  • feature 와 encoder는 모두 이전 학습시 사용된 데이터에 의해 고정된 이후 사용되기 때문에, cluster 생성만 할 뿐, labeled data가 주는 이점을 반영하지 못함.

  Deep TEN은 이런 문제점들을 Residual Encoding Layer를 통해 해결했습니다. 이제부터 그 개념을 하나씩 살펴보겠습니다.

  

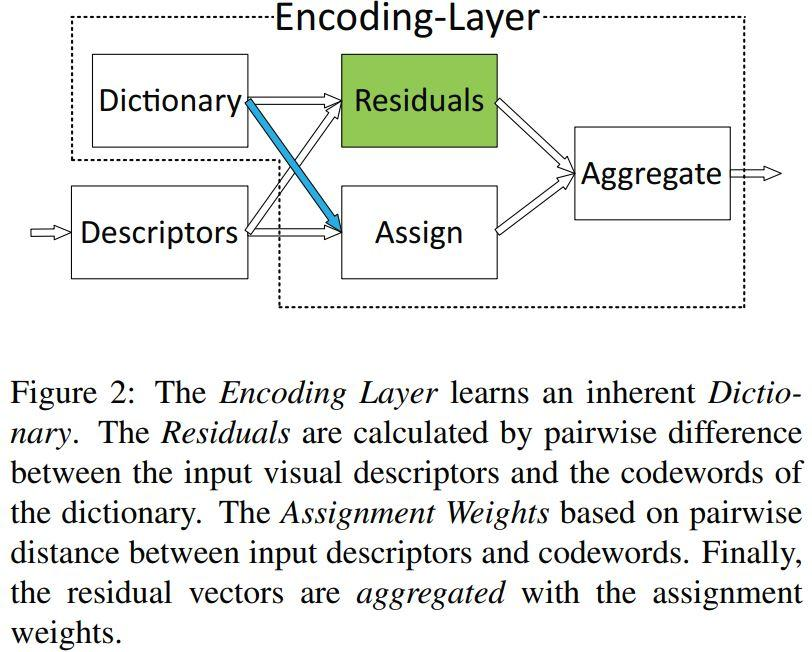
  H. Zhang, J. Xue, and K. Dana. Deep ten: Texture encoding network. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), July 2017.

  전체 흐름을 이해하기에 앞서, 논문이 사용하는 ‘residual vector’에 대해 설명하고 넘어가겠습니다.

  N개의 descriptor(feature)로 구성된 visual Descriptor set X = {x1, x2, …., xi} 와 K개의 codeword로 구성된 codebook set C = {c1, c2,….,ck} 를 가정해보겠습니다. 이 때, 각 codeword에 대해 descritor xi 는 연관관계를 정의하는 weight aik (i 번째 descriptor와 k번째 codeword 간의 weight)와 residual vector rik = xi - ck 로 표현할 수 있습니다.  이런 개념을 바탕으로 residual encoding model이 하는 일은 k개의 codeword에 대해 다음과 같은 aggregation operation을 수행하는 일입니다.

  

  수식 1

  즉, 특정 code word에 대해 이번 input에서 얻어낸 N개의 모든 descrptor와의 weight와 residual vector를 곱해 더함으로써 고정된 길이 (code word의 길이 k) 의 encoded representation을 얻어내는 것입니다. 그 결과, 이제 이 encoding layer는 input의 갯수와 무관하면서 order-less한 일종의 ‘pooling’을 수행할 수 있게 되었습니다.

  이 encoded representation이 어떤 역할을 하는지, 논문에서 제공한 간단한 예시를 통해 이해해보겠습니다.

  어떤 이미지 A에서 descriptor xi 가 많이 관찰되었다고 가정해보겠습니다.  이는 곧, descriptor xi가 center에 분포하고 있는 특정 cluster center ck에 가깝다는 뜻이 됩니다. 그렇다는 것 곧, 이 descriptor xi 와 codeword ck 사이를 정의하는 residual vector rik = xi - ck 가 작다는 것을 의미합니다.  잠시 weight aik 를 정의하는 식을 살펴보겠습니다.

  

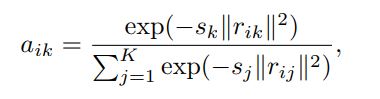
  수식 2

  수식 2는 각 descriptor에 대해 codeword를 soft assign하는 수식입니다. Soft-weight assignment 는 서로 다른 cluster 들이 대략적으로 비슷한 크기를 가진다고 가정한 뒤(논문에서는 이 점을 들어 Encoding Layer가 Gaussian Mixture Model의 simplified version이라고 볼 수 있다고 말하고 있습니다), scaling(smoothing) factor sk 가 학습될 수 있도록 네트워크를 디자인해 좀 더 정확한 modeling이 가능하도록 했습니다. 이 식에 따르면 위에서 언급된 예시의 경우, descriptor xi의, ck가 아닌 다른 codeword(j != k) 대한 residual vector(rij)에는 상대적으로 작은 weight가 할당되게 됩니다.

  여기까지가 Deep TEN이 가지고 있는 기본 아이디어라고 할 수 있을 것 같습니다. 위에서 설명한 것 같은 구조적 특징으로 인해 생긴 Deep Ten의 인상적인 기능(?)을 설명하는 것으로 포스팅을 마무리 짓겠습니다.

  • Pooling Layer: CNN의 기존 pooling layer들이 고정된 receptive field를 사용하며 특정 크기의 input size만 받아들일 수 있는 것과 달리, residual encoding layer는 input을 고정된 길이의 distribution으로 변화시키기 때문에, arbitrary input size를 받아들일 수 있다는 장점이 있습니다.
  • Multi-size Training: 위의 장점에서 더 나아가 Deep TEN은 fixed length feature representation을 이용해 multi-size training을 시도했습니다. 352x352, 320x320의 두 가지 사이즈의 이미지로 training시켰을 때, network의 performance가 상승한다는 것이 논문의 실험을 통해 증명되었습니다.
  • Joint Deep Encoding: 논문이 제시한 residual encoding layer는 conv layer의 앞단에서 domain-independent한 feature를 추출하는 역할을 합니다. 논문은 서로 다른 두가지 재질 데이터셋에 대해 두 개의 분리된 encoding layer로 추출한 convolutional feature들이 서로 공유되도록 네트워크를 설계, performance가 소량 상승한다는 것을 증명했습니다.

  Deep TEN은 결과적으로 최근 널리 사용되는 몇 가지 재질 데이터셋 (MINC-2500, GTOS, KTH, 4D-Light)에 대해 발표 당시 기준 STOA를 찍은 논문입니다.

• Code Book의 역할이 뭘까? 그게 channel별(혹은 cluster별) 대표값 정도이고 앵커 역할을 학습할때 수행해서 구심점 역할을 하는 것

• Bag of Words?

  출처: https://darkpgmr.tistory.com/125

  먼저 참고한 자료는 다음과 같습니다.

  • 위키피디아: Bag of Words Model in Computer Vision (BoW에 대한 전반적인 내용)
  • Li Fei-Fei, Rob Fergues, Antonio Torralba, “Recognizing and Learning Object Categories”, ICCV 2005 short course (iccv 2005 best short course award)
  • [Csurka04] G. Csurka, C. Dance, L.X. Fan, J. Willamowski, and C. Bray. ”Visual categorization with bags of keypoints“, ECCV 2004. (기본적인 BoW 방법)
  • [Lazebnik06] Lazebnik, S.; Schmid, C.; Ponce, J., “Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories“ CVPR 2006. (Spatial Pyramid Matching 기법)
  • [Lampert08] C. H. Lampert, M. M. Blaschko, and T. Hofmann, “Beyond Sliding Windows: Object Localization by Efficient Subwindow Search” CVPR 2008. (ESS 기법, cvpr 2008 best paper award)

  1. Bag of Words 기법

  원래 Bag of Words 기법은 문서(document)를 자동으로 분류하기 위한 방법중 하나로서, 글에 포함된 단어(word)들의 분포를 보고 이 문서가 어떤 종류의 문서인지를 판단하는 기법을 지칭한다. 예를 들어, 어떤 문서에서 ‘환율’, ‘주가’, ‘금리’ 등의 단어가 많이 나온다면 이 문서는 경제학에 관련된 문서로 분류하고 ‘역광’, ‘노출’, ‘구도’ 등의 단어가 많다면 사진학에 대한 문서로 분류하는 방식이다.

  영상처리, 컴퓨터 비전 쪽에서는 Bag of Words 기법을 주로 이미지를 분류(image categorization)하거나 검색(image retrieval)하기 위한 목적으로 사용하였는데, 최근에는 물체나 씬(scene)을 인식하기 용도로도 폭넓게 활용되고 있다.

  https://t1.daumcdn.net/cfile/tistory/253363395302B4A60F

  <그림 1> 그림출처: Recognizing and Learning Object Categories (ICCV 2005 short course)

  영상 분류를 위한 Bag of Words 방법은 먼저 영상에서 feature(주로 SIFT 등의 local feature)들을 뽑은 후, 이들 feature들을 대표할 수 있는 값(code)들로 구성되는 코드북(codebook)을 생성한다. 보통 코드북은 다수의 이미지들로부터 추출한 feature들 전체에 대해 클러스터링(k-means clustering)을 수행하여 획득한 대표 feature(각 cluster의 center)들로 구성된다. 이 코드북은 일종의 단어 사전(dictionary)으로 볼 수 있는데, 이 사전에는 가능한 모든 종류의 단어들이 포함되어 있는 것이 아니라 물체나 이미지를 분류하는데 있어서 중요하다고 생각되는 주요 단어들만이 포함되어 있는 점이 다르다. 코드북에 포함된 단어를 코드워드(codeword)라 부르는데, 코드북을 몇 개의 codeword로 구성할 지는 조절 가능한 파라미터로서 영상 feature들을 몇개의 클러스터로 클러스터링할지에 따라 결정된다.

  일단 코드북이 완성되면 이제 각각의 이미지들을 이 코드북을 이용하여 표현(representation)할 수 있게 된다. 어떤 이미지 A가 있을 때, 먼저 A로부터 feature들을 추출한 후 추출된 각각의 feature들에 대해 코드북 내에서 대응되는(가장 유사한) 코드워드(codeword)를 찾는다. 그리고 이렇게 찾은 코드워드들의 히스토그램(histogram)으로 이 이미지의 특징을 표현한다 (그림 1).

  이렇게 구한 코드워드의 히스토그램(각각의 코드워드가 이미지에서 몇번 나타났는지 개수를 센 것)이 동일 종류의 물체에 대한 이미지들 사이에서는 유사하고 다른 종류의 물체에 대해서는 서로 다를 것이라는 것이 Bag of Words를 이용한 이미지 분류의 핵심 아이디어이다 (그림 2).

  https://t1.daumcdn.net/cfile/tistory/2171564C5302BF5F27

  <그림 2> 그림출처: Recognizing and Learning Object Categories (ICCV 2005 short course)

  이상의 Bag of Words 방법을 이용한 이미지 분류 과정을 정리해 보면 다음과 같다.

  1. Feature Extraction: 이미지들로부터 feature를 추출한다 (SIFT 등)
  2. Clustering: 추출된 feature들에 대해 클러스터링을 수행하여 클러스터 센터(center)들인 codeword들을 찾아낸다. 클러스터링 방법은 보통 k-means clustering이 사용된다.
  3. Codebook Generation: 찾아진 codeword들로 구성되는 코드북을 생성한다. 코드북은 물체 클래스마다 생성하는 것이 아니라 <그림 2>의 예와 같이 공통적으로 하나만 생성되며 모든 클래스의 codeword들을 포함한다.
  4. Image Representation: 각각의 이미지들을 codeword들의 히스토그램으로 표현한다. 이미지 하나당 하나의 히스토그램이 나오며 이 히스토그램의 크기(bin의 개수)는 코드북의 크기(코드북을 구성하는 codeword들의 개수)와 동일하다.
  5. Learning and Recognition: BoW 기반의 학습 및 인식 방법은 크게 Bayesian 확률을 이용한 generative 방법과 SVM 등의 분류기를 이용한 discriminative 방법이 있다. Bayesian 방법은 물체 클래스별 히스토그램 값을 확률로서 해석하여 물체를 분류하는 것이고, discriminative 방법은 히스토그램 값을 feature vector로 해석하여 SVM(support vector machine)등의 분류기에 넣고 클래스 경계를 학습시키는 방법이다.

  Bag of Words 기법은 통상적으로 local feature에 대한 히스토그램을 사용하지만 사실 어떤 영상 feature를 사용하느냐에 따라서 다양한 활용이 가능하다. 예를 들어, 색상(color)을 가지고 과일을 분류하는 문제를 생각해 보자. 먼저 분류하고자 하는 모든 과일 사진들을 한꺼번에 모아놓고 색상 값들을 추출한다. 패치(patch)단위로 색상을 추출할 수도 있고 픽셀 단위로 추출할 수도 있을 것이다. 이렇게 모은 색상값들을 모두 한데 놓고 클러스터링 알고리즘을 적용하여 대표 색상값들을 추출한다. 만일 분류하고자 하는 과일이 사과, 딸기, 수박, 오렌지 였다면 대표 색상값으로는 초록색, 빨강색, 노란색, 오렌지색 계열의 색상들이 뽑혔을 것이다. 이렇게 추출한 대표 색상들을 모아놓은 것이 코드북(codebook)이며 대표 색상을 100개 뽑았다면 이 코드북의 크기는 100이 된다. 만일 RGB 색상 모델을 사용한다고 했을 때, R, G, B 각각이 0 ~ 255 사이의 값을 가질 수 있기 때문에 가능한 모든 색의 종류는 256256256 = 16,777,216 가지나 된다. 하지만 이 코드북 상에는 과일색을 대표할 수 있는 색상 100개만이 포함되어 있다. 이제 어떤 새로운 이미지가 들어왔을 때 이 이미지의 색상값들을 코드북상에서 가장 유사한 대표색으로 대체한다. 즉, 입력 이미지 상의 모든 색들 각각을 코드북 상의 100개의 색상 중의 하나로 대체한다. 그리고 이렇게 대체된 색들의 히스토그램이 어떤 과일의 히스토그램과 유사한지를 비교함으로써 새로운 이미지가 어떤 과일인지를 판단한다.

  2. Spatial Pyramid Matching

  Bag of Words 방법[Csurka04]은 영상의 카테고리를 분류하는 용도, 주어진 이미지와 유사한 영상을 찾는 용도 등으로 성공적으로 적용되어 왔다. 또한 씬 매칭(scene matching) 등을 할 때 가능성이 적은 후보 영상들을 걸러내는 용도로도 효과적으로 활용되고 있다.

  하지만 Bag of Words 방법은 기본적으로 feature들의 히스토그램(histogram)으로 이미지를 표현하기 때문에 feature들간의 기하학적인 위치 관계를 잃어버리는 문제점을 가지고 있다. 물론 동물 등과 같이 변형이 심한 물체를 인식하는데는 이 특성이 오히려 장점으로 작용하지만 자동차 등과 같이 형태가 고정된 물체의 경우에는 성능저하의 큰 요인중 하나가 될 수 있다.

  2006년 Lazebnik 등이 발표한 Spatial Pyramid Matching 방법[Lazebnik06]은 이러한 Bag of Words 방법의 단점을 보완하기 위한 대표적인 방법 중 하나이다.

  Spatial Pyramid Matching 방법은 이미지를 여러 단계의 resolution으로 분할한 후 각 단계의 분할 영역마다 히스토그램을 구하여 이들을 전체적으로 비교하는 방법을 일컫는다. 그림을 통해 보면 <그림 3>의 오른쪽 그림(level 0)은 이미지 전체에 대해서 하나의 히스토그램을 구하는 경우로서 전통적인 Bag of Words 기법이 이에 해당한다. 하지만 Spatial Pyramid Matching 방법에서는 여기에 추가적으로 이미지를 점진적으로 세분(level 1에서는 2x2로 분할, level 2에서는 4x4로 분할, …)해 가면서 각각의 분할 영역마다 별도로 히스토그램을 구한 후 , 이들 히스토그램들을 전부 모아서 일종의 피라미드(pyramid)를 형성한다. 그리고 이렇게 형성된 히스토그램 피라미드들을 서로 비교함으로써 두 이미지의 유사도를 측정하는 방식이다.

  https://t1.daumcdn.net/cfile/tistory/2407DA485302FE6009

  <그림 3> 출처: [Lazebnik06]

  물론 히스토그램을 구하는 과정은 Bag of Words 프레임워크 내에서 이루어진다. 즉, 미리 visual feature들에 대한 코드북을 생성한 후 이 코드북 코드들에 대해서 히스토그램을 생성한다 (위 그림 3은 코드북의 크기가 3인 경우의 예를 보여주고 있다). 유사도 측정에 대해 좀더 자세히 설명하면, 입력 이미지에 대해 level 0에서 생성한 히스토그램을 h0, level 1에서 생성한 히스토그램들을 순서대로 h1_0, h1_1, h1_2, h1_3, level 2에서 생성한 히스토그램들을 h2_0, h2_1, …, h2_15라 하자(문제에 따라서 level 2까지만 구할 수도 있고 그 이상의 level에 대해서 히스토그램을 구할 수도 있다). 이 때, 모델(사전에 학습시킨) 이미지에서 계산한 히스토그램들을 h0’, h1_0’, h1_1’, …, h2_15’라 한다면 h0와 h0’의 유사도를 측정하고, h1_0와 h1_0’의 유사도를 측정하고, … 와 같이 서로 대응되는 히스토그램의 유사도를 측정한 후 이들을 전체적으로 종합하여 입력 이미지와 모델(model) 이미지의 유사도를 측정하는 방식이다. 이 때, 높은 레벨(좀더 세분화된 분할)에서 측정된 유사도에 좀더 높은 가중치를 줌으로써 feature 분포의 공간(위치) 정보가 유지될수록 높은 점수를 주는 것이 일반적이다.

  ☞ Spatial Pyramid Matching에 대한 구체적인 수식이나 세부 구현에 대해서는 [Lazebnik06] 논문을 참조하기 바라며, 이러한 기법은 Bag of Words 프레임워크 내에서 뿐만 아니라 다른 일반적인 히스토그램 기반의 매칭 문제에도 유사하게 적용될 수 있음을 참고하기 바랍니다.

  ☞ 히스토그램 간의 유사도를 측정하는 방법에는 Bhattacharyya distance, Earth mover’s distance (EMD), histogram intersection 등이 있는데, BoW 계열에서는 histogram intersection(두 히스토그램의 대응되는 bin의 최소값들을 전부 합한 값)이 주로 사용되는 것 같습니다.

  3. Beyond Sliding Windows: Efficient Subwindow Search 기법

  [Lampert08] C. H. Lampert, M. M. Blaschko, and T. Hofmann, “Beyond Sliding Windows: Object Localization by Efficient Subwindow Search” CVPR 2008

  ☞ 저를 몇 주간 괴롭히던 논문이자 2008년도 CVPR 학회에서 Best Paper 상을 탔던 논문입니다. 처음 논문을 읽으면서는 ‘이게 정말 이렇게 돼?’, ‘이게 정말 된다면 엄청난 것 같은데’ 하는 생각을 하였고 이제 어느정도 윤곽을 파악한 지금도 참 대단한 논문이라는 생각은 변치 않습니다. 다만 그 적용이 Bag of Words 계열의 문제에 국한된다는 점이 아쉬울 따름입니다.

  Sliding Window 기법은 영상에서 물체를 찾는데 가장 기본적으로 사용되는 기법으로서, 영상에서 윈도우(window)를 일정한 간격으로 이동시키면서 윈도우 내의 영상 영역이 찾고자 하는 물체인지 아닌지를 판단하는 방법이다. 찾고자 하는 물체가 영상내 어떤 위치와 어떤 크기로 있는지를 모르기 때문에 가능한 모든 영상 위치 및 크기(image pyramid의 각 scale마다 sliding window 탐색을 적용)에 대해 물체의 존재 여부를 반복적으로 검사하는 exhaustive searching 방법이 Sliding Window 기법의 본질이다.

  https://t1.daumcdn.net/cfile/tistory/223B4250530318D528

  <그림 4>

  이러한 sliding window 탐색은 거의 모든 영상 물체 탐색(object localization) 방법들에서 공통으로 사용하고 있지만 그 엄청난 반복 검사로 인해 알고리즘의 속도를 현저히 느리게 하는 가장 큰 주범이기도 하다.

  그런데, [Lampert08] 논문에서는 이러한 반복 검사 없이도 sliding window 방법과 동일한 결과를 낼 수 있는 ESS 탐색 방법을 소개하고 있다 (논문 저자들은 이 탐색 방법을 Efficient Subwindow Search (ESS)라 부르기 때문에 여기서도 이후로는 ESS라 부른다).

  Sliding Window 기법에서는 보통 어떤 평가함수 f가 있어서 윈도우 영역(r)마다 f(r)값을 조사하여 임계값(threshold value) 이상이면 대상 물체가 있는 것으로 판단한다. 하지만, ESS에서는 탐색영역 R에 대한 평가함수 F가 존재하여 F(R) 값이 큰 영역을 우선적으로 탐색하는 방법을 사용한다. 먼저, 처음에는 입력 영상 전체를 R로 놓고 F 값을 계산한다. 이후 탐색 영역을 둘로 분할한 후 각각에 대해 F 값을 계산하여 F 값이 최대인 영역을 선택하고 이를 다시 둘로 분할한다. 이와 같이 현재의 후보 영역들 중에서 F 값이 가장 큰 영역을 선택하여 그 영역을 둘로 분할하는 과정을 계속하다가 더이상 쪼갤 수 없는 단위 윈도우가 나올 때까지 진행하면 global optimum을 찾게 된다는 방식이다. 일종의 best first search 방식으로서, 이들의 주장이 맞다면 F 값이 높은 영역들에 대해서만 검사를 진행하기 때문에 훨씬 적은 수의 evaluation 만으로도 대상 물체를 찾을 수 있게 된다.

  F 값을 어떻게 잡느냐를 알아보기 전에 이 논문에서 탐색영역을 어떻게 정의하고 또 어떻게 분할하는지를 먼저 살펴보자.

  탐색영역 R은 사각형 윈도우들의 집합으로서 4개의 범위 값으로 정의되는데, 아래 그림과 같이 사각형을 정의하는 top, bottom, left, right 4개 값에 대한 상한과 하한으로 정의된다.

  https://t1.daumcdn.net/cfile/tistory/2223EF4B53032D7B26

  https://t1.daumcdn.net/cfile/tistory/2124E55053032BE927

  <그림 5> 출처: [Lampert08]

  즉, 탐색영역 R은 어떤 영상 영역 내에 특정 범위의 모든(scale 변화까지 포함한) window들의 집합으로 볼 수 있으며 탐색영역 R을 둘로 분할하는 방법은 T,B,L,R 중에서 가장 범위가 큰 구간을 둘로(절반으로) 쪼개는 것이다. => 이렇게 탐색영역을 정의하는 방법도 참 기발한 것 같습니다.

  다음으로 탐색영역 R에 대한 평가함수 F를 어떻게 잡느냐에 대해 살펴보자. F(R)은 직관적으로는 탐색영역 R 내에 물체가 있을 확률을 추정한 값으로 볼 수 있는데, 논문에서는 F가 다음의 두 가지 조건만 만족하면 앞서 설명한 best first search 방식으로도 sliding window search와 동일한 결과를 얻을 수 있다고 주장한다.

  https://t1.daumcdn.net/cfile/tistory/21269C3D530363C234

  즉, i) F(R)은 탐색영역 R 내에서 가능한 모든 윈도우 r에 대한 f(r) 값들의 상한이 되어야 하고, 또한 ii) 만일 R이 단일 윈도우만으로 구성된 경우에는 해당 윈도우에 대한 f(r) 값과 동일한 값이 나와야 한다는 뜻이다.

  f(r)은 어느 하나의 윈도우 영역이 물체인지 아닌지를 평가한 값이지만 F(R)은 R에 포한되는 다양한 윈도우 영역들에 대한 f(r) 값들을 직접 계산하지 않고도 이들의 상한을 추정한 값이다.

  처음에는 위 조건이 무언가 문제가 있는 것이 아닌가 하는 생각이 들었다. 왜냐하면 global 해를 찾기 위해서는 다음과 같은 세번째 조건이 추가적으로 필요하다고 생각했기 때문이다.

  https://t1.daumcdn.net/cfile/tistory/2339BD395303696611

  그래야만, F(R) 값이 높은 R을 선택했을 때 실제 f(r) 값이 높은 윈도우가 포함된 R이 선택될 거라고 생각했다. 하지만 나중에는 조건 iii)은 전혀 필요가 없으며 조건 i) & ii) 만으로 충분함을 깨닫게 되었는데, 그 오해의 원인은 ESS 탐색 과정을 일부 잘못 이해하고 있었기 때문이었다. ESS 알고리즘을 다시 적어보면 다음과 같다.

  1. 현재의 후보 탐색영역들을 R1, R2, …, Rk라 하자 (초기에는 하나의 후보 탐색영역만이 존재하며 그것은 입력영상 전체이다)
  2. 후보 탐색영역들 중에서 F(Ri) 값이 가장 큰 Ri을 선택한 후, 만일 Ri이 단일 윈도우로 구성된다면 global optimum으로 Ri을 반환하고 탐색을 종료한다. 그렇지 않은 경우에는 Ri을 두개의 영역으로 분할하여 후보 리스트에 추가한 후 탐색 과정을 반복한다.

  즉, 핵심은 어떤 탐색영역(실제 물체가 포함되어 있는)이 현재 단계에서는 선택받지 못했더라도 후보 리스트 내에서 계속 경쟁을 하다보면 언젠가는 선택을 받게 된다는 점이다. 예를 들어, 두 탐색영역 R1, R2가 있고 R1에 포함된 윈도우들의 f값의 최대값이 30, R2에 포함된 윈도우들의 f값의 최대값이 40, R1의 추정값이 F(R1) = 60, R2에 대한 추정값이 F(R2) = 50라 하자. 그러면 현재는 추정값이 더 큰 R1을 선택하여 탐색을 진행하겠지만 R1을 계속 분할해 나가다 보면 조건 ii)에 의해서 언젠가는 반드시 추정값이 F(R2)보다 작아지는 순간이 오고 그 때부터는 R2가 선택되어 탐색이 진행된다. 결국 최종적으로는 f가 최대인 윈도우가 선택되게 된다.

  이상으로, 조건 i), ii)만 만족하면 ESS 탐색으로 global 해를 찾을 수 있음은 알게 되었다. 하지만 문제는 이러한 F를 실제 어떻게 잡을 수 있느냐이다.

  사실 이러한 조건을 만족하는 F는 무수히 많이 존재한다. 먼저, F를 잡는 한 극단적인 예는 F를 R에 관계없이 굉장히 큰(모든 가능한 r에 대한 f(r) 값보다 큰) 상수값으로 잡고 R이 단일 윈도우로 구성될 때에만 F(R) = f(r)이 되도록 하는 것이다. 이 경우 F(R)은 항상 동일한 값이므로 어떤 유용한 정보도 제공하지 않기 때문에 결과적으로 ESS는 exhaustive 탐색과 같게 된다. 다른 극단적인 예는 F(R)이 R에 포함된 윈도우들의 f값의 실제 최대값이 되도록 잡는 것이다. 이 경우 ESS 자체는 global 해가 있는 쪽으로 일직선으로 탐색이 진행되는 가장 효율적인 탐색이 되겠지만 F(R)을 계산하기 위해서는 R에 포함된 모든 윈도우들의 f값을 계산해야 하기 때문에 결과적으로는 exhaustive 탐색이 되어 버린다. 즉, 결론적으로 F는 이 두 양극단의 사이에 있는 어떤 값이 되어야 하며 F가 실제 f값의 최대값에 근접할수록 ESS 탐색은 효율적이 되지만 그만큼 F를 계산하기는 더 어려워지는 trade off가 존재한다.

  [Lampert08] 논문에서는 세가지 실제 문제들에 대해서 구체적으로 F를 잡는 예를 설명하고 있다. 보다 자세한 내용은 [Lampert08] 논문을 참조하기 바란다.

  A. 전통적인 bag of words 방법에의 적용

  기존의 bag of words 방법은 물체의 존재 여부만 확인해 줄 뿐 물체의 정확한 위치는 알 수 없었다. 하지만 ESS 방법을 적용하면 빠르게 물체를 찾을 수 있을 뿐만 아니라 물체의 정확한 위치까지도 파악이 가능하다. 즉, object localization 목적으로 적용이 가능해진다. 그 방법은 다음과 같다.

  학습 영상에서 bag of words 방식으로 추출한 feature 히스토그램들을 feature 벡터로 보고 SVM(support vector machine)으로 학습시켜서 나온 support vector들을 hi, 대응되는 weight를 αi라 했을 때, 어떤 입력 윈도우 r에 대한 SVM evaluation 값 f(r)은 r에서 계산한 feature 히스토그램을 h라 했을 때 f(r) = ∑αi(h·hi) + β = ∑j (∑i αihcji) + β가 된다 (단, cj는 feature j가 속하는 cluster index, j = 1, 2, …, n는 r 내의 모든 feature). 이 때, f = f+ + f- (f+: ∑i αihcji가 +인 term들의 합, f-: ∑i αihcji가 -인 term들의 합)로 f를 분해했을 때, F(R) = f+(r_max) + f-(r_min)로 정의하면 조건 i) & ii)를 만족시키기 때문에 ESS 적용이 가능해진다 (단, r_max는 R 내에서 가장 큰 윈도우, r_min은 최소 윈도우).

  B. Spatial Pyramid Matching 방식에의 적용

  ESS를 spatial pyramid matching에 적용하는 방법은 약간 더 복잡하긴 하지만 기본적으로는 bag of words 경우와 동일하다.

  먼저, SVM 학습 단계에서는 pyramid matching kernel을 구성하는 각각의 분할별로 각각 SVM을 학습시킨다. 즉, 원래의 모델 영상을 level 0에서는 1x1 블록으로 분할하고, level 1에서는 2x2 블록으로 분할하고, …, level l에서는 2lx2l 블록으로 분할한다고 했을 때, 모든 level의 모든 블록에 대해 각각 SVM을 하나씩 학습시킨다. 그리고 이렇게 얻어진 SVM의 decision hyperplane들을 모두 더하여(선형 결합) 최종 SVM classifier를 구성한다. 만일 level l의 (i,j) 번째 블록에 대한 SVM decision hyperplane이 f_l,(i,j)(r) = ∑α_l,(i,j)k*(h·h_l,(i,j)k) + β_l,(i,j)라면 최종 SVM classifier는 f(r) = ∑_l,i,j f_l,(i,j)(r_l,(i,j))가 된다 (r_l,(i,j)는 윈도우 r을 pyramid 형태로 분할했을 때, level l의 (i,j)번째 분할 영역을 나타낸다). 이제 탐색영역 R에 대한 추정값 F(R)은 R을 pyramid 형태로 분할했을 때 각각의 분할영역에서 계산된 F_l,(i,j) 값들을 모두 합한 값으로 계산한다. 이 때, 각각의 분할영역에서의 F_l,(i,j) 값은 그 영역에서의 최대 윈도우를 r_max, 최소 윈도우를 r_min이라 했을 때 f+_l,(i,j)(r_max) + f-_l,(i,j)(r_min)로 계산된다 (=> 사실 논문에서는 이렇게까지 구체적으로 설명되어 있지는 않습니다만 나름의 방식으로 정리해 보았습니다).

  C. Image Retrieval에의 응용

  마지막으로 ESS를 이미지 검색에 활용하는 예에 대해 살펴보자. 어떤 질의(query) 이미지 패치(patch) Q가 있을 때 비디오나 이미지 DB에서 Q를 포함하는 이미지를 모두 검색하는 것이 풀고자 하는 문제이다.

  기본적으로는 Q에 대한 feature 히스토그램 hQ와 이미지 I의 모든 가능한 윈도우 영역 r에 대해 생성한 feature 히스토그램 hr을 비교하여 계산된 히스토그램 유사도의 최대값이 높은 이미지들을 선택하는 방법을 사용한다. 두 히스토그램간의 유사도 측정은 Χ2-distance를 사용한다. 이 때, Q와 이미지 I의 유사도는 Similarity(Q,I) = max{ -Χ2(hQ, hr)

  r⊆I }로 계산된다. 그런데, 실제 Similarity(Q,I)를 계산하기 위해서는 I 내의 모든 가능한 r에 대해서 Χ2(hQ, hr) 값을 계산해야만 하지만 ESS를 적용하면 exhaustive evaluation을 하지 않고도 유사도를 측정할 수 있으며 또한 I 내에서 가장 유사도가 높은 윈도우를 찾아낼 수 있다. 이를 위해서는 유사도에 대한 추정값이 실제 유사도에 대한 상한이 되도록 식을 정의해야 하는데, 그 구체적인 수식은 논문을 참조하기 바란다.

  4. 맺음말

  영상에서 물체를 찾는 방법은 feature들 간의 기하학적인 관계를 정확하게 매칭하는 방법(homography를 이용한 SIFT 매칭 등)과 bag of words 기법을 이용하여 feature들의 히스토그램을 매칭하는 방법으로 크게 구분할 수 있습니다. 초창기에는 기하학적 매칭 방법이 대세를 이루었으나 이후 bag of words 방식이 출현한 이후로는 한동안은 사람들의 관심이 BoW 쪽으로 집중되었던 것 같습니다. 이러한 배경에는 기존의 기하학적 매칭 방법이 동일 물체의 인식에만 국한되고 또한 카메라의 시점 변화에 매우 민감한 문제가 있기 때문일 것입니다. 반면에 BoW 방법은 동일 물체가 아니라 동일 카테고리의 물체를 식별하는데 적용될 수 있고 또한 시점 변화에 매우 강인한 특성을 가지고 있기 때문에 좀더 높은 평가를 받은 것으로 보입니다. 하지만 최근에는 feature들 간의 spatial 정보를 잃어버린다는 BoW의 장점이자 단점이 갖는 성능상의 한계를 극복하기 위하여 다시 기하학적인 관계를 활용하는 방향으로의 연구가 활성화되고 있다고 합니다. 개인적으로는 어쩌면 이 두가지 특성을 모두 결합하여 활용하는 방안을 연구하는 것이 가장 좋은 방향이 아닌가 생각됩니다.

• scene 내부에 있는 objects들이 어떤 class들에 해당하는지 특정 class별로 어떤 label로 출력해내는 것
  • Encoding

• Q> 일종의 Multi task learning 이라고 볼 수 있을까? classification이랑 object detection이랑 같이 학습할때 성능향상이 있다 그런식의 논문도 좀 있거든요

• 인풋피쳐 차원: C
• X: H*W에 대해서 하나씩 의미 하는 것 같다.
  • N = H*W
  • X_i → D_k 자체도..
• cluster
  • 실제 github code 봤을 때는 32로 설정되어 있었음..

ri = x_i - c_k

L2 scale과는 다르게..

scaling

smoothing factor:

• code-book cluster : code-book 자체를 cluster 의미
• k: cluster 의 갯수

• 이 네트워크는 a scene에서, 각각의 Semantic Component들의 Semantic label을 pixel-wise로 예측하지만, Global context를 고려하진 못한다.
  • 따라서 이를 보완하기 위해 다음 SE-loss를 추가해주었다.
    • Encoded semantics가 정말로 scene에 존재했던 objects들을 예측해냈는지를 정량적으로 판단하여, 틀리면 패널티를 주는 방식이다.
      • Encoder가 Scene에 있는 objects categories 후보들을 정확하게 예측할 수 있게 학습하도록 돕는다.

• Ablation study: (pixACC(%), mIoU(%) 두 지표에서 모두 성능 증가)
  • Encoding context 모듈을 추가했을 때 (73.1%→78.1%)
  • SE-loss를 추가했을 때
  • Deeper Backbone network를 사용했을 때

(Class가 많아서)

Conclusion

• contextual information을 잡아내고 활용하기 위해, Contex Encoding Module을 도입하였고,
  • 이 모듈은 선별적으로 클래스-의존적인 (class-dependent) featuremap를 강조(Scaling)해주면서, 네트워크의 ‘ ‘ 문제를 단순화 해줬습니다.
• light-weight (1/10의 layer수)이면서도, 기존의 FCN 방식과 비등한 성능을 보여주었습니다.
• 실험 결과는 EncNet의 우수한 성능을 보여줍니다.