ECCV 2020. [Paper] [Project] [Github]
Jiapeng Zhu, Yujun Shen, Deli Zhao, Bolei Zhou
The Chinese University of Hong Kong
31 Mar 2020
Introduction
Recently, GAN models have learned how to encode rich semantics within the latent space, making it possible to manipulate corresponding attributes of output images by changing latent codes. However, since GANs lack the ability to take a specific image as input and extract its latent code, manipulating output images by changing latent codes is difficult to apply to real images. As a result, many attempts have been made to perform GAN inversion, which maps the image space back to the latent space, opposite to the GAN’s generation process. These attempts include training an additional encoder attached to the GAN or directly searching for individual image latent codes. However, these methods focus only on pixel-level restoration of input images, raising various questions, such as:
- Whether the inverted code is suitable for the original GAN’s latent space
- Whether the inverted code semantically represents the target image well
- Whether the inverted code reuses the knowledge learned by the GAN to support image editing
- Whether the inverted code of arbitrary images can be found using a well-trained GAN Being able to answer these questions will not only deepen our understanding of GAN’s internal mechanisms but also allow us to utilize pre-trained GAN models for various image editing tasks.
This paper demonstrates that a good GAN inversion method should not only restore the target image but also align the inverted code with the semantic knowledge encoded in the latent space. Such semantically meaningful codes are dependent on the semantic domain learned by the GAN, referred to as in-domain codes. The authors discovered that in-domain codes can better reuse the rich knowledge of existing GAN models for image editing, and they proposed in-domain GAN inversion that reconstructs the input image at both pixel and semantic levels.
The entire learning process consists of two steps:
To ensure that all codes generated by the encoder are in-domain, they first train a domain-guided encoder that maps the image space to the latent space. They then perform instance-level domain-regularized optimization with the encoder as a regularizer to reconstruct pixel values more accurately without changing the semantic attributes of the inverted code.
In-Domain GAN Inversion
When inverting a GAN model, it is necessary to consider not only restoring the input image to pixel values but also whether the inverted code is semantically meaningful. Here, ‘semantic’ refers to the knowledge that GAN learns from the data. To achieve this, a domain-guided encoder is first trained, and this encoder is used as a regularizer for domain-regularized optimization.
In the conventional GAN model, a latent code $z$ is drawn from a normal distribution $\mathcal{Z}$ and fed into the generator. In the StyleGAN model, a normal distribution $\mathcal{Z}$ is mapped to a latent space $\mathcal{W}$ using an MLP, and a $w$ drawn from $\mathcal{W}$ is fed into the generator. This mapping allows for learning more disentangled semantics, so the disentangled space $\mathcal{W}$ is generally used for GAN inversion. In this paper, $\mathcal{W}$ was chosen as the inversion space for three reasons:
- The focus is on the semantic properties of the inverted code, so the $\mathcal{W}$ space is suitable for analysis.
- Inverting to the $\mathcal{W}$ space shows better performance than inverting to the $\mathcal{Z}$ space.
- Any GAN model can use the $\mathcal{W}$ space by simply adding an MLP in front of it.
1. Domain-Guided Encoder
Training an encoder is commonly used to solve the GAN inversion problem due to its fast inference speed. However, existing methods simply train a deterministic model regardless of whether the code generated by the encoder matches the semantic knowledge learned by the GAN.
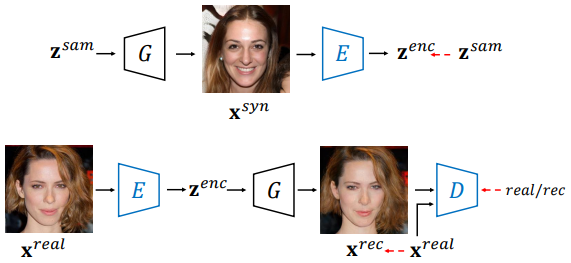
The figure above shows the conventional encoder training method at the top and the domain-guided encoder training method at the bottom. The blue-highlighted model blocks are the blocks being trained.
Conventional methods draw $z^{sam}$, feed it into the generator to synthesize $x^{syn}$, and then train the encoder so that the output $z^{enc}$ is close to the ground truth $z^{sam}$.
\[\begin{equation} \min_{\Theta_E} \mathcal{L}_E = \| z^{sam} - E(G(z^{sam})) \|_2 \end{equation}\]| ($\Theta_E$ is the encoder’s parameter, $$ | \cdot | _2$$ is the $l_2$ distance) |
Restoring $z^{sam}$ alone is not enough to train an accurate encoder. Additionally, the generator’s gradient is not considered at all, making it impossible to provide domain knowledge. To solve these problems, a domain-guided encoder needs to be trained. There are three differences between the domain-guided encoder and the conventional encoder:
- The output of the encoder is input into the generator, and the image is reconstructed, so the objective function comes from the image space rather than the latent space. This includes the semantic knowledge learned by the generator, providing more useful and accurate supervision. As a result, it guarantees that the output code belongs to the generator’s semantic domain.
- The domain-guided encoder is trained with real images rather than synthesized images from the generator, making it more suitable for real applications. To ensure that the reconstructed image is realistic enough, the discriminator competes with the encoder.
- This approach allows for obtaining as much information as possible from the GAN model. The adversarial training method produces an output code that better matches the generator’s semantic knowledge.
($P_{data}$ is the actual data distribution, $\gamma$ is the hyper-parameter for gradient regularization, $\lambda_{vgg}$ and $\lambda_{adv}$ are weights for perceptual loss and discriminator loss, $F$ is the VGG feature extraction model)
Domain-Regularized Optimization
Unlike the generative process of GANs that learn mapping from latent distribution to actual image distribution, GAN inversion is closer to an instance-level task that reconstructs given individual images best. From this perspective, it is difficult to learn perfect reverse mapping with just an encoder, as its expressive power is limited. Therefore, the inverted code of the domain-guided encoder can ensure that it reconstructs the input image well based on the pre-trained generator and is semantically meaningful. Still, the code must be further adjusted to fit individual target images better.
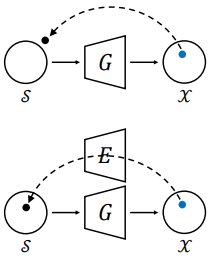
Existing methods optimized the code using gradient descent. In the figure above, the top case is a process where the latent code is freely optimized based on the generator only. Since there are no constraints on the latent code, the possibility of generating inverted codes outside the domain is very high. There are two improvements to the domain-regularized optimization designed using the domain-guided encoder:
- Use the output of the domain-guided encoder as an ideal starting point to prevent the latent code from stopping at local minima and significantly shorten the optimization process.
- Include the domain-guided encoder as a regularizer to preserve the latent code within the generator’s semantic domain.
The objective function for optimization is as follows:
\[\begin{equation} z^{inv} = \underset{z}{\arg \min} \| x - G(z) \|_2 + \lambda_{vgg} \| F(x) - F(G(z)) \|_2 + \lambda_{dom} \| z - E(G(z)) \|_2 \end{equation}\]($x$ is the target image to be inverted, $\lambda_{vgg}$ and $\lambda_{dom}$ are weights for perceptual loss and encoder regularizer)
Experiments
- Dataset: FFHQ (70,000 images), LSUN (10 scene types)
- Generator: StyleGAN (used fixed)
- Perceptual loss uses VGG conv4_3
- Loss weight: $\lambda_{vgg} = 5\times 10^{-5}$, $\lambda_{adv} = 0.1$, $\gamma = 10$, $\lambda_{dom} = 2$
1. Semantic Analysis of the Inverted Codes
7,000 real face images were predicted for age (young vs. old), gender, presence of glasses, and pose (left, right) attributes using an attribute classifier and used as ground truth. The images were then inverted into latent space using the state-of-the-art GAN inversion model Image2StyleGAN and the in-domain GAN inversion model proposed by the authors. InterFaceGAN was used to find semantic boundaries for attributes, and the performance of attribute classification was evaluated using these boundaries and inverted codes.
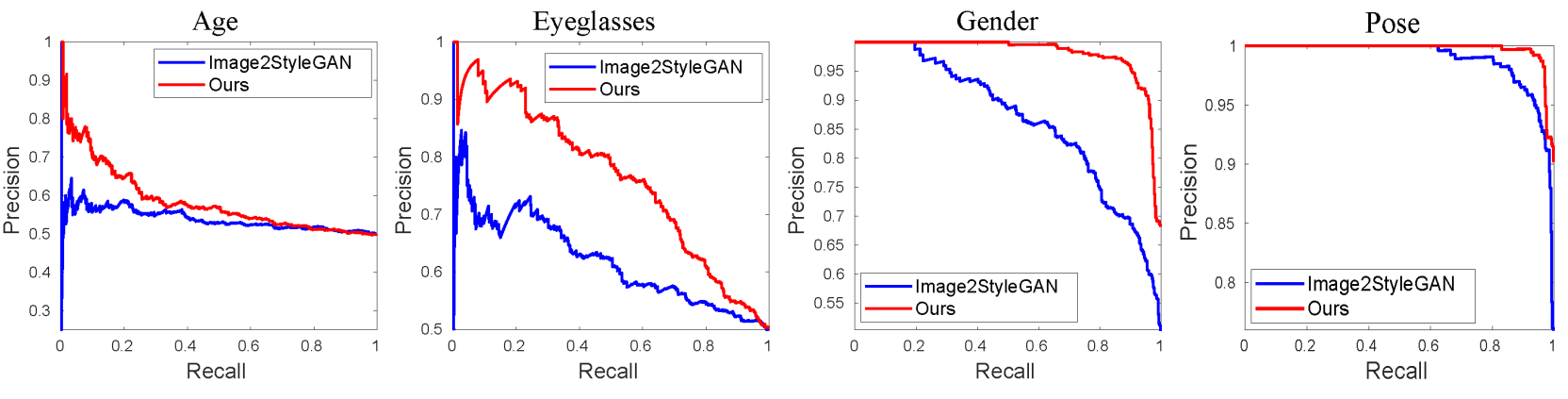
The graph above shows the precision-recall curve for each semantic. As can be seen from the graph, it can be concluded that the inverted codes of the in-domain GAN inversion model are semantically meaningful. This quantitatively proves the effect of in-domain inversion in preserving semantic properties of inverted codes.
2. Inversion Quality and Speed


3. Real Image Editing - Image Interpolation


4. Real Image Editing - Semantic Manipulation
In the specific semantic latent space, let the normal direction be $n$ and the manipulation degree be $\alpha$. Then, semantic manipulation is possible with the following linear transformation:
\[\begin{equation} x^{edit} = G(z^{inv} + \alpha n) \end{equation}\]

The top row of each image is the result of Image2StyleGAN, and the bottom row is the result of in-domain inversion.
The following are the results of incorporating the semantic of the context image into the target image.

Ablation study

The above figure shows the results depending on the value of $\lambda_{dom}$. The top row is the original image, the second row is the restored image, and the bottom row is the manipulated image. The larger the value of $\lambda_{dom}$, the less well the restoration is done, but the better the manipulation is done.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)