arXiv 2022. [Paper]
Weilun Wang, Jianmin Bao, Wengang Zhou, Dongdong Chen, Dong Chen, Lu Yuan, Houqiang Li
University of Science and Technology of China (USTC) | Microsoft Research Asia | Microsoft Cloud+AI
30 Jun 2022

Introduction
Semantic image synthesis aims to create a real-life image based on a semantic layout, and is the opposite problem of semantic segmentation. Recent work mainly follows an adversarial learning paradigm in which networks are trained with adversarial loss along with reconstruction loss. Progressively improve performance on a benchmark dataset by exploring the model architecture. However, existing GAN-based approaches have limitations in producing high fidelity and diverse results in some complex scenes.
DDPM (Denoising Diffusion Probabilistic Model) is a new kind of generative model based on maximum likelihood learning. DDPM generates samples from a standard Gaussian distribution to an empirical distribution through an iterative denoising process. State-of-the-art sample quality was achieved in several image production benchmarks through incremental improvement of the generated results.
In this paper, we present the first attempt to explore a diffusion model for the problem of semantic image synthesis and design a new framework called Semantic Diffusion Model (SDM). The framework follows the denoising diffusion paradigm and converts sampled Gaussian noise into realistic images through an iterative denoising process. The generation process is a parameterized Markov chain. Noise is estimated from the input noisey image by the denoising network adjusted according to the semantic label map at each step. According to the estimated noise, an image with less noise is generated through the posterior probability formula. Through repetition, the denoising network gradually generates semantic-related content and injects it into the denoising stream to create realistic images.
We revisit the previous conditional DDPM, which directly connects the conditional information to the noisy image as input to the denoising network. Since this approach does not fully utilize the information of the input semantic mask, the semantic correlation with the quality of the generated image is low as in previous studies. Motivated by this, we design a conditional denoising network that independently processes semantic layout and noisy images. The noisy image is fed into the denoising network’s encoder while the semantic layout is embedded in the denoising network’s decoder by means of a multi-layer spatially-adaptive normalization (SPADE) operator. This greatly improves the quality and semantic correlation of the generated images.
Diffusion models can also produce inherently diverse results. Sampling strategy plays an important role in balancing the quality and variety of the results produced. Naive sampling procedures can produce images that show high diversity but lack realism and robust correspondence with semantic label maps. Adopt the Classifier-free guidance strategy to improve image fidelity and semantic correspondence. In particular, the semantic mask input is randomly removed to fine-tune the pre-learned diffusion model. A sampling strategy is then processed based on the prediction of the diffusion mask with and without a semantic mask. By interpolating the scores of these two situations, the sampling result achieves higher fidelity and stronger correlation with the semantic mask input.
Methodology
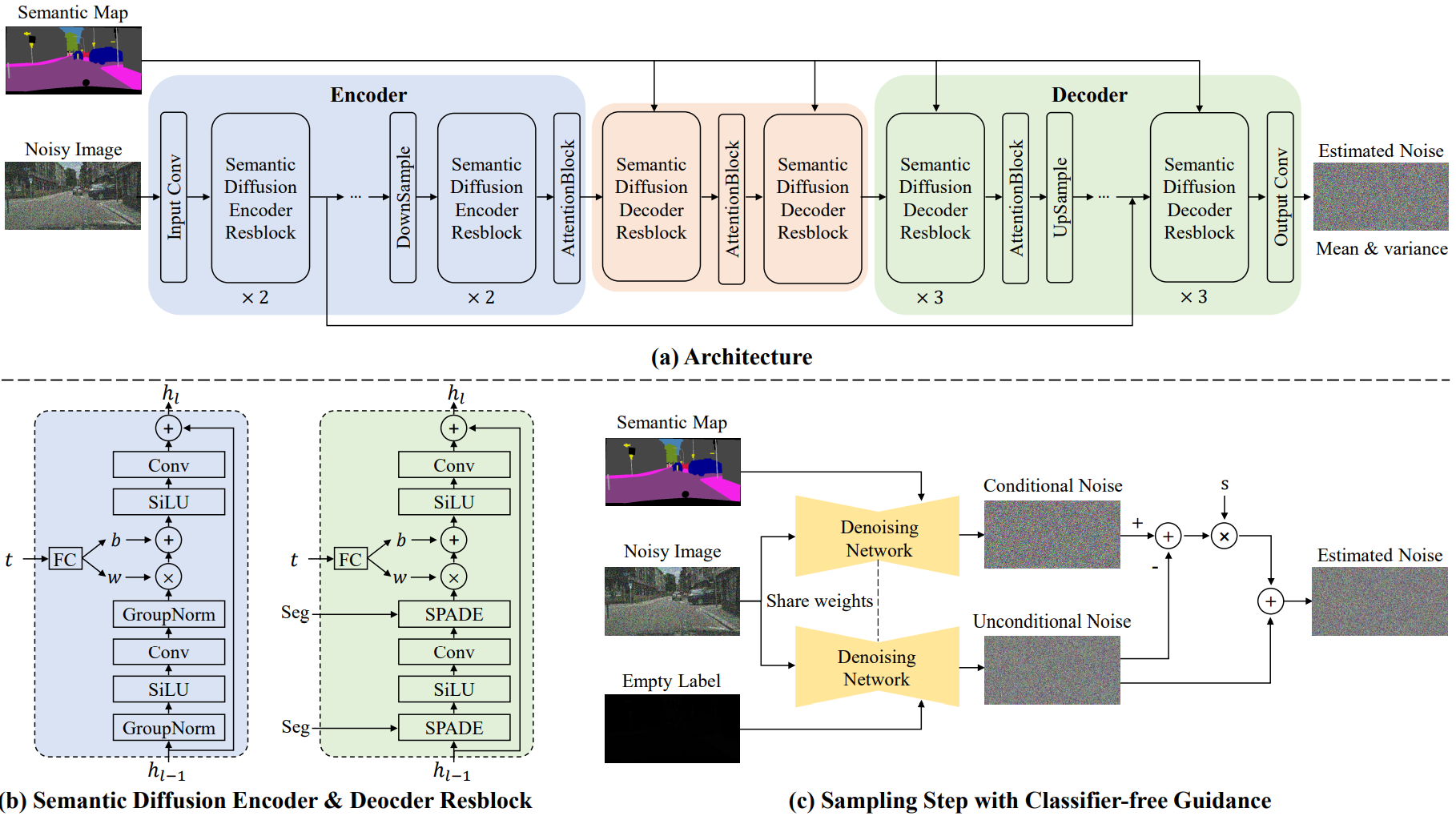
1. Semantic Diffusion Model
Figure (a) above is an overview of the conditional denoising network of SDM. Unlike the conventional conditional diffusion model, the denoising network processes semantic label maps and noisy images independently. The noisy image goes into the encoder part and the semantic label map is injected into the decoder as a multi-layer SPADE operation.
Encoder
The features of the noisy image are encoded with the semantic diffusion encoder resblock (SDEResblock) and attention block. (b) in the figure above shows the detailed structure of SDEResblock, which consists of convolution, SiLU, and group normalization. SiLU is an activation function that tends to perform better than ReLU in deep models, and f(x) = x \cdot \textrm{sigmoid}(x)$. To force the network to estimate the noise at multiple timesteps $t$, SDEResblock uses the intermediate activations as learnable weights $w(t) \in \mathbb{R}^{1 \times 1 \times C}$ and bias $b( t) scaled and shifted to \in \mathbb{R}^{1 \times 1 \times C}$.
\[\begin{equation} f^{i+1} = w(t) \cdot f^i + b(t) \end{equation}\]$f^i, f^{i+1} \in \mathbb{R}^{H \times and \times C}$ are the input and output features, respectively. Attention block is a self-attention block with skip-connection.
\[\begin{equation} f(x) = W_f x, \quad g(x) = W_g x, \quad h(x) = W_h x \\ \mathcal{M} (u, v) = \frac{f(x_u)^\top g(x_v)}{\|f(x_u)\| \|g(x_v)\|} \\ y_u = x_u + W_v \sum_v \textrm{softmax}_v (\alpha \mathcal{M}(u,v)) \cdot h (x_v) \end{equation}\]$x$ and $y$ are the inputs and outputs of the attention block, and $W_f, W_g, W_h, W_v \in \mathbb{R}^{C \times C}$ is a 1$\times$1 convolution block. $u$ and $v$ are spatial dimension indices, ranging from 1 to $H \times W$. Attention block is applied only at a specific resolution. (32$\times$32, 16$\times$16, 8$\times$8)
Decoder
We guide the denoising process by injecting the semantic label map into the denoising network denoising. In the existing conditional diffusion model, condition information and noisy input are directly concated and used as input. The authors found that this approach does not make full use of semantic information. To solve this problem, a semantic diffusion decoder resblock (SDDResblock) is designed to embed the semantic level map into the decoder in a multi-layer spatially-adaptive method. Unlike SDEResblock, it uses spatially-adaptive normalization (SPADE) instead of group normalization. SPADE injects a semantic level map into the denoising stream.
\[\begin{equation} f^{i+1} = \gamma^i (x) \cdot \textrm{Norm} (f^i) + \beta^i (x) \end{equation}\]$\textrm{Norm}$ is group normalization without parameters. $\gamma^i (x)$ and $\beta^i (x)$ are spatially-adaptive weights and biases. SDM is different from SPADE because it is designed for diffusion process including attention block, skip-connection, and timestep embedding modules.
3. Loss functions
The SDM is trained with two objective functions. The first objective function is the simple diffusion loss. Given a reference output image $y$ and a random timestep \(t \in \{0, 1, \cdots, T\}\), a noisy version $\tilde{y}$ of $y$ is generated as do.
\[\begin{equation} \tilde{y} = \sqrt{\vphantom{1} \bar{\alpha}_t} y + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]$\alpha_t$ is the noise schedule at $t$. Let $T = 1000$ in SDM. The conditional diffusion model is trained to reconstruct $y$ by predicting noise $\epsilon$ under the guidance of the semantic layout $x$.
\[\begin{equation} \mathcal{L}_\textrm{simple} = \mathbb{E}_{t, y, \epsilon} = [\| \epsilon - \epsilon_\theta(\sqrt{\vphantom{1} \bar{\alpha}_t} y + \sqrt{1 - \bar{\alpha}_t} \epsilon, x, t) \|_2] \end{equation}\]Following the Improved DDPM, the network is additionally trained to predict the variance $\Sigma_\theta (\tilde{y}, x, t)$, improving the log-likelihood of the generated images. The conditional diffusion model additionally outputs the interpolation coefficient $v$, and the variance is as follows.
\[\begin{equation} \Sigma_\theta (\tilde{y}, x, t) = \exp (v \log \beta_t + (1-v) \log \tilde{\beta}_t) \end{equation}\]The second objective function is the KL between the estimated distribution $p_\theta (y_{t-1} \vert y_t, x)$ and the posterior probability of the diffusion process $q(y_{t-1} \vert y_t, v_0)$ Optimize the divergence directly.
\[\begin{equation} \mathcal{L}_\textrm{vlb} = \textrm{KL} (p_\theta (y_{t-1} \vert y_t, x) \| q (y_{t-1} \vert y_t, y_0)) \end{equation}\]The total loss is the weighted sum of the two objective functions.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{simple} + \lambda \mathcal{L}_\textrm{vlb} \end{equation}\]$\lambda$ is a trade-off parameter to balance the loss function.
4. Classifier-free guidance.
If you follow the general sampling process of DDPM, images are created in various ways, but they are not realistic and are not strongly related to the semantic label map. The authors hypothesize that the conditional diffusion model does not handle conditional inputs well during the sampling process. Previous studies have improved the sample of the conditional diffusion model with a log probability gradient.
\[\begin{equation} \nabla_{y_t} \log p(x \vert y_t) \end{equation}\]If the estimated mean is $\mu_\theta (y_t \vert x)$ and the estimated variance is $\Sigma_\theta (y_t \vert x)$, we can perturb the mean to improve the result as follows:
\[\begin{equation} \hat{\mu}_\theta (y_t \vert x) = \mu_\theta (y_t \vert x) + s \cdot \Sigma_\theta (y_t \vert x) \cdot \nabla_{y_t} \log p (x \vert y_t) \end{equation}\]$s$ is a hyperparameter called the guidance scale, which compromises sample quality and variability.
In the previous work, an additionally learned classifier $p(x \vert y_t)$ was applied to provide the gradient during the sampling process. Inspired by the Classifier-free Diffusion Guidance paper, guidance is obtained with the generative model itself instead of a classifier model that requires extra cost to train. The main idea is to replace the semantic label map $x$ with a null label $\emptyset$ to estimate according to the guidance of $\epsilon_\theta (y_t \vert x)$ in $\epsilon_\theta (y_t \vert \emptyset)$ isolate the generated noise. Separate elements implicitly infer the gradient of the log probability.
\[\begin{aligned} \epsilon_\theta (y_t \vert x) - \epsilon_\theta (y_t \vert \emptyset) & \propto \nabla_{y_t} \log p (y_t \vert x) - \nabla_{y_t} \log p (y_t) \\ & \propto \nabla {y_t} \log p (x \vert y_t) \end{aligned}\]During the sampling process, this discrete factor is increased to improve the sample of the conditional diffusion model.
\[\begin{equation} \tilde{\epsilon}_\theta (y_t \vert x) + s \cdot (\epsilon_\theta (y_t \vert x) - \epsilon_\theta (y_t \vert \emptyset)) \end{equation}\]In this paper, $\emptyset$ is defined as a zero vector.
Experiments
- Dataset: Cityscapes (256$\times$512) / ADE20K, CelebAMask-HQ, COCO-Stuff (256$\times$256) -Evaluation
- Visual Quality: FID (Frechet Inception Distance)
- Diversity: LPIPS
- Correspondence: Evaluate semantic interpretability with commercial networks
- Cityscapes uses DRN-D-105, ADE20K uses UperNet101, CelebAMask-HQ uses Unet, and COCO-Stuff uses DeepLabV2
- Calculate mIoU (mean IoU) with the generated image and semantic layout
- mIoU depends on the capabilities of commercial networks
1. Comparison with previous methods
The following is a quantitative evaluation table with existing methods for semantic image synthesis.
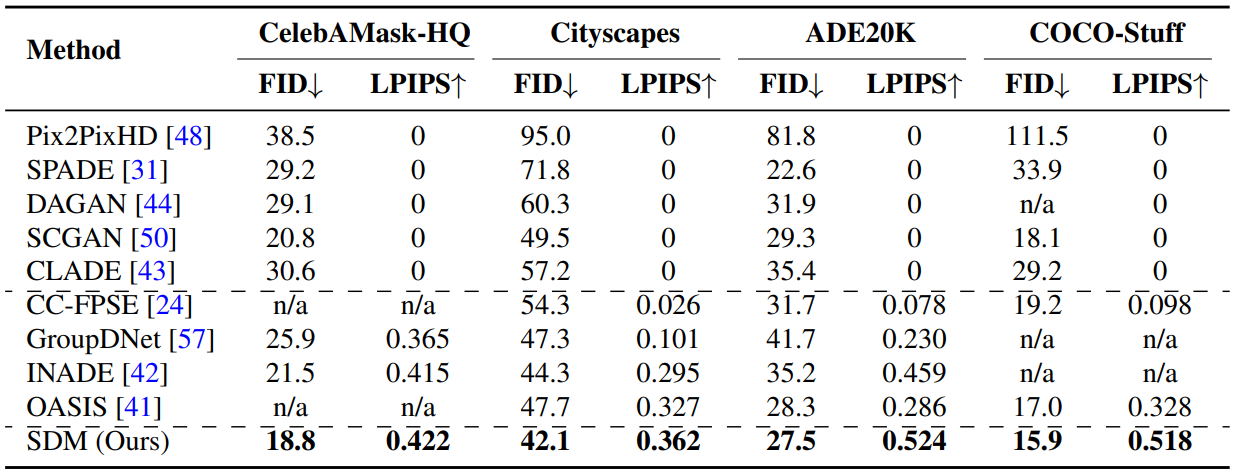
Next up are CelebAMask-HQ, ADE20K, and Cityscapes. Samples from COCO-Stuff were compared.




The following is a user study showing the ratio of preferring the results of this paper to the results of various other methods for the four datasets.

The following is the multimodal generation result created with the model of this paper. It can be seen to produce a variety of high-quality results.

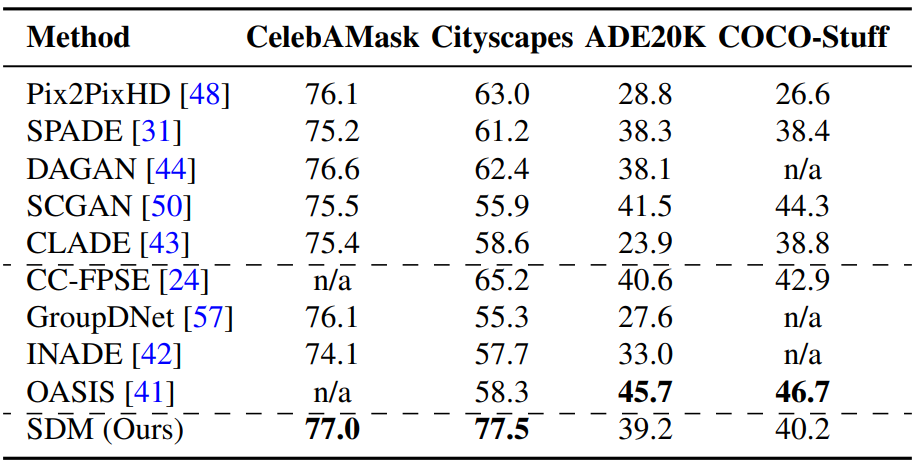
The following table shows the measured mIoU for the four datasets.
2. Ablation Studies
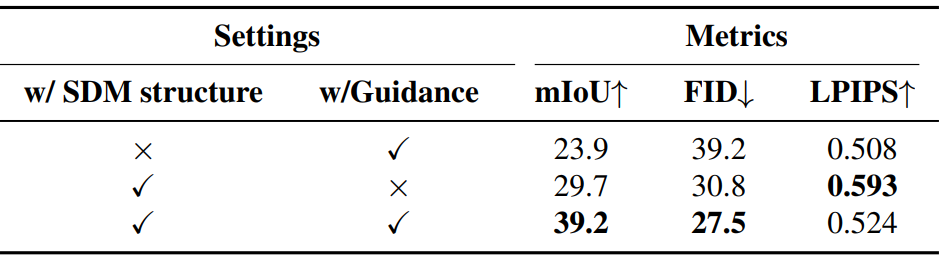
The following is the result of the ablation study on the embedding of condition information and the classifier-free guidance strategy.
The following is a comparison of the qualitative results of the ablation experiment.

3. Controlled Generation
The following is an example of SDM’s semantic image editing. The green part is the erased part, and the model performs inpainting based on the edited semantic map.








![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)