ACM TOG 2022. [Paper] [Github]
Daniel Roich, Ron Mokady, Amit H. Bermano, Daniel Cohen-Or
The Blavatnik School of Computer Science, Tel Aviv University
10 Jun 2021

Introduction
In recent years, unconditional image synthesis has made tremendous progress with the advent of GANs. In essence, a GAN learns the domain (or manifold) of a set of desired images and creates new samples from the same distribution. In particular, StyleGAN is one of the most popular options for this task. It not only achieves state-of-the-art visual fidelity and versatility, but also exhibits fantastic editing capabilities due to organically formed disentangled latent space. Using this property, many methods pass through the learned manifold to show the realistic editing capabilities of StylGAN’s latent space, such as changing face orientation, expression or age.
Impressively, these edits are performed strictly in the latent space of the generator and cannot be applied to real images outside that domain. So, editing real images starts with finding the latent representation. This process, called GAN inversion, has recently attracted considerable attention. An early attempt inverted the image into $\mathcal{W}$, which is StyleGAN’s default latent space. Image2stylegan, however, found that inverting a real image into this space causes distortion, i.e. a discrepancy between the given image and the generated image, resulting in artifacts such as loss of identity or unnatural appearance. appeared to occur. Therefore, current inversion methods often use an extended latent space, denoted by $\mathcal{W}+$, which is more expressive and introduces much less distortion.
However, while using the codes in $\mathcal{W}+$ can potentially produce great visual quality even for out-of-domain images, these codes are not editable because they are not in the generator’s learned domain. e4e defines this collision as a distortion-editability trade-off and shows that the closer the code is to $\mathcal{W}$, the more editable it is. Indeed, a recent paper proposes a compromise between editability and distortion by choosing the latent code of editable $\mathcal{W}+$.
In this paper, we introduce a novel approach that mitigates the distortion-editability trade-off, allowing persuasive editing of undistributed real-world images. Instead of projecting an input image onto a learned manifold, we slightly change the generator to enlarge the manifold to contain the image. This process is called Pivotal Tuning. This tuning is similar to shooting a dart and then moving the board itself to compensate for a melee hit.
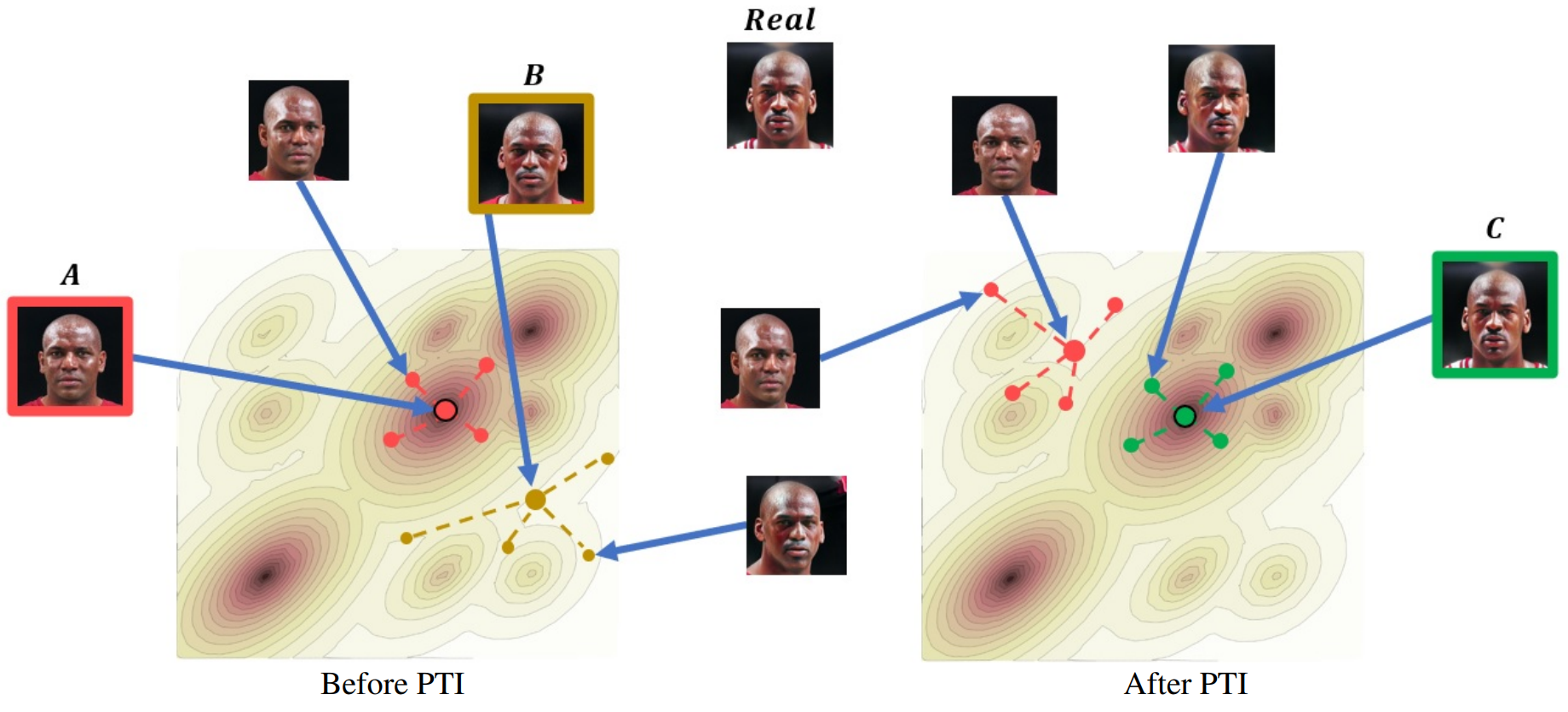
Because StyleGAN training is expensive and the generator achieves unprecedented visual quality, a popular approach is to keep the generator stationary. In contrast, this paper proposes to create a personalized version of the generator that accepts the desired input image. The approach of this paper consists of two main steps. First, the input image is inverted into an editable latent code using conventional inversion technology. Of course, this produces an image that is similar to the original, but not necessarily identical. In the second step, pivotal tuning is performed. Lightly tune the pre-trained StyleGAN so that the input image is generated when using the pivot latent code found in the previous step (see figure above). The key idea is that the latent code maintains editorial quality even if the generator is slightly modified. The modified generator maintains the editability of the pivot code while achieving unprecedented reconstruction quality. Pivotal tuning moves the identity of the central region to the desired region with minimal impact by performing local operations in the latent space. In order to further minimize side effects, only the surgical adaptation of the latent space is performed by introducing a regularization term. This creates a generator that can edit multiple target IDs without interference.
Method
The method of this paper seeks to provide high-quality editing for real images using StyleGAN. The key idea of the approach is that due to the disentangle nature of StyleGAN, we can apply slight local changes to the generated shape without compromising its powerful editing capabilities. Therefore, if an image is likely to fall out of distribution in terms of appearance, we propose to find the nearest editable point within the generator domain. This pivot point can then be pulled towards the target, with minimal effect on the surroundings and negligible effect elsewhere.
We present a two-step method for converting real images into highly editable latent code. First, the given input in StyleGAN’s default latent space $\mathcal{W}$ is inverted into $w_p$. Then, Pivotal Tuning is applied to this pivot code $w_p$ to adjust the pretrained StyleGAN to generate the desired image for the input $w_p$. The intuition here is that since $w_p$ is close enough, training the generator to generate the input image at the pivot can be achieved by augmenting only the shape-related weights without affecting the well-behaved structure of StyleGAN’s latent space.
1. Inversion
The purpose of the inversion step is to provide a convenient starting point for pivotal tuning. As mentioned earlier, StyleGAN’s default latent space $\mathcal{W}$ provides the best editability. Because of this and because distortion is reduced during pivotal tuning, we invert the given input image $x$ into this space instead of the more widely used $\mathcal{W}+$ expansion. The authors use the existing inversion method proposed by StyleGAN2. Essentially, a direct optimization is applied to optimize both the latent code $w$ and the noise vector $n$ to reconstruct the input image $x$ measured by the LPIPS perceptual loss function. As described in StyleGAN2, optimizing the noise vector $n$ using the noise normalization term significantly improves inversion because the noise normalization prevents important information from being included in the noise vector. This means that once $w_p$ is determined, the $n$ value plays a small role in the final visual appearance. Overall, optimization is defined by the objective function:
\[\begin{equation} w_p, n = \underset{w, n}{\arg \min} [\mathcal{L}_\textrm{LPIPS} (x, G(w, n; \theta)) + \lambda_n \mathcal{L}_n (n)] \end{equation}\]Here $G(w, n; \theta)$ is the image created with generator $G$. It does not use StyleGAN’s mapping network. \(\mathcal{L}_\textrm{LPIPS}\) is the perceptual loss and $\mathcal{L}_n$ is the noise regularization term. At this stage the generator is fixed.
2. Pivotal Tuning
Applying the latent code $w$ obtained from inversion produces an image similar to the original $x$, but with considerable distortion. So, in the second step, we unfreeze the generator and tune it to reconstruct the input image $x$ given the latent code $w$ obtained in the first step called pivot code $w_p$. It is important to use a pivot code because convergence fails if a random or average latent code is used. Let $x^p = G(w_p; \theta^\ast)$ be the image created using $w_p$ and the tuned weights $\theta^\ast$. Fine-tune the generator using the following loss terms:
\[\begin{equation} \mathcal{L}_{pt} = \mathcal{L}_\textrm{LPIPS} (x, x^p) + \lambda_{L2} \mathcal{L}_{L2} (x, x^p) \end{equation}\]Here the generator is initialized with pretrained weights $\theta$. At this stage, $w_p$ is constant. Pivotal Tuning performs $N$ images \(\{x_i\}_{i=0}^N given $N$ inverted latent code\){w_i}_{i=0}^N\(Can be expanded to\).
\[\begin{equation} \mathcal{L}_{pt} = \frac{1}{N} \sum_{i=1}^N (\mathcal{L}_\textrm{LPIPS} (x_i, x_i^p) + \lambda_{ L2} \mathcal{L}_{L2} (x_i, x_i^p)) \\ x_i^p = G (w_i; \theta^\ast) \end{equation}\]Once the generator is tuned, you can edit the input image by selecting a latent space editing technique.
3. Locality Regularization
When Pivotal Tuning is applied to Latent Code, the generator actually reconstructs the input image with high accuracy and enables successful editing. At the same time, Pivotal Tuning triggers ripple effects. That is, the visual quality of images produced by non-local latent code is compromised. This is especially true when tuning for multiple IDs. To mitigate this side effect, we introduce a regularization term designed to constrain the PTI change to a local region in latent space. At each iteration, a normally distributed random vector z is sampled and the corresponding latent code w_z = f(z) is generated using StyleGAN’s mapping network f. Then we interpolate between $w_z$ and the pivotal latent code $w_p$ using the interpolation parameter $\alpha$ to obtain the interpolated code $w_r$.
\[\begin{equation} w_r = w_p + \alpha \frac{w_z - w_p}{\| w_z - w_p \|_2} \end{equation}\]Finally, the image $x_r = G(w_r; \theta)$ generated by giving $w_r$ as input using the original weights and the image $x_r^\ast = G(w_r; $x_r^\ast = G(w_r; Minimize the distance between \theta^\ast)$.
\[\begin{equation} \mathcal{L}_R = \mathcal{L}_\textrm{LPIPS} (x_r, x_r^\ast) + \lambda_{L2}^R \mathcal{L}_{L2} (x_r, x_r^\ast) ) \end{equation}\]This can be extended to $N_r$ random latent codes.
\[\begin{equation} \mathcal{L}_R = \frac{1}{N_r} \sum_{i=1}^{N_r} (\mathcal{L}_\textrm{LPIPS} (x_{r, i}, x_{r, i}^\ast) + \lambda_{L2}^R \mathcal{L}_{L2} (x_{r,i}, x_{r,i}^\ast)) \end{equation}\]The new optimization is defined as:
\[\begin{equation} \theta^\ast = \underset{\theta^\ast}{\arg \min} [ \mathcal{L}_{pt} + \lambda_R \mathcal{L}_R ] \end{equation}\]Here, $\lambda_{L2}^R$, $\lambda_R$, and $N_r$ are hyperparameters.
Experiments
- Generator: pre-trained at FFHQ
1. Reconstruction Quality
Qualitative evaluation
The following are reconstruction results for samples outside the domain.

Here is a comparison of reconstruction quality for an example from the CelebA-HQ dataset.

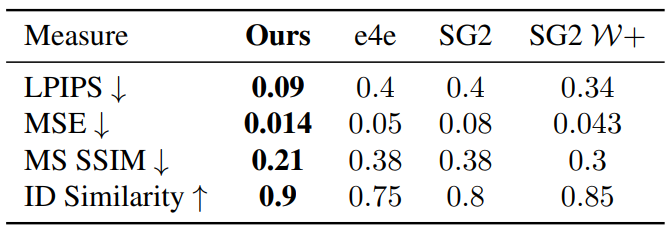
Quantitative evaluation
The following is a qualitative comparison result for reconstruction quality.
2. Editing Quality
Qualitative evaluation
The following is a comparison of editing results for images in the CelebA-HQ dataset.

Here’s a comparison of the results of editing celebrity photos collected from around the web.

The following is a comparison of editing results for images outside the domain collected from the web. (smile, age, beard removal)

The following is an example of sequential editing. (rotation, smile)

Here is an example of additional editing. Hair and pose are edited on the left, hair and age are edited in the middle, and pose and smile are edited on the right.

The following are examples of actual image editing using Multi-ID Personalized StyleGAN.

The following is an example of “Friends” StyleGAN.

The following is a comparison of editing results with and without PTI when editing with StyleClip. (bowl cut, mohawk)

The following is a comparison of the editing results with or without PTI when editing using StyleClip and InterfaceGAN sequentially. (Top: Bob cut hair, smile, rotation / Middle: bowl cut hair, older / Bottom: curly hair, younger, rotation)

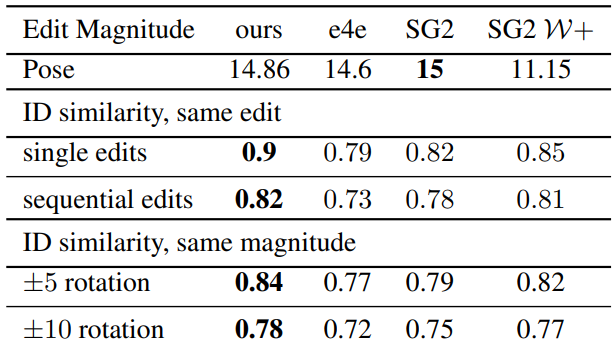
Quantitative evaluation
The following is a quantitative evaluation of the editing results.
3. Regularization
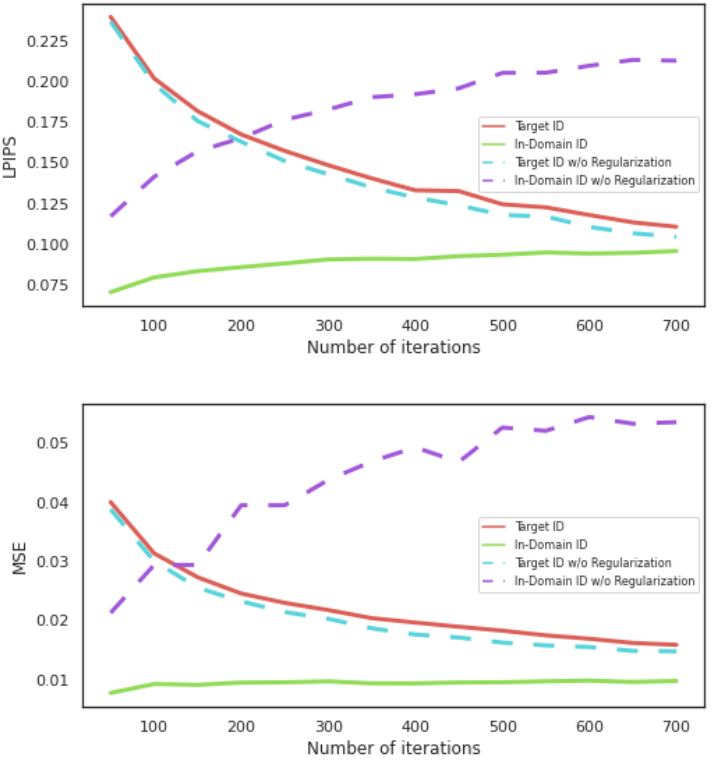
The following shows the effect of locality regularization on random latent code for pivotal tuning applied to multiple IDs.

The following is the quantitative evaluation result of locality regularization.
4. Ablation study
The following is the result of the ablation study applying the same editing to smile (top) and pose (bottom).

- (A): Same as the method of this paper
- (B): invert to $\mathcal{W}+$ instead of $\mathcal{W}$ in first step
- (C): Replace Pivot latent code $w_p$ with average latent code $\mu_w$
- (D): Replace $w_p$ with random latent code
- (E): initialize $w_p$ to $\mu_w$ and optimize with generator
- (F): initialize $w_p$ with random latent code and optimize with generator







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)