Blogs

CVPR 2023. [Paper] [Page]
Qinsheng Zhang, Jiaming Song, Xun Huang, Yongxin Chen, Ming-Yu Liu
Georgia Institute of Technology | NVIDIA Corporation
30 Mar 2023

Introduction

Diffusion model의 성공은 확장성 때문일 수 있다. 대규모 데이터셋과 컴퓨팅 리소스를 사용하여 일반적으로 고화질 이미지를 생성할 수 있는 고용량 모델을 학습시킬 수 있다. 큰 데이터셋을 수집하고 이를 사용하여 대규모 모델을 학습시키는 동일한 절차가 다양한 문제에 적용되어 큰 성공을 거두었다.

본 논문은 diffusion model의 성공을 더 넓은 종류의 데이터로 확장하는 데 관심이 있다. 저자들은 타겟 콘텐츠의 대규모 데이터셋이 존재하지 않거나 수집하는 데 엄청나게 많은 비용이 들지만 콘텐츠의 개별 부분을 대량으로 사용할 수 있는 애플리케이션에 중점을 둔다. 360도 파노라마 이미지가 그러한 예이다. 360도 파노라마 이미지는 소량만 존재하지만 인터넷에는 일반 투시 이미지가 많이 있으며 각 이미지는 360도 파노라마 이미지의 일부로 취급될 수 있다.

또 다른 예는 극단적인 종횡비의 이미지를 생성하는 것이며, 일반 종횡비의 여러 이미지를 연결한 것으로 간주할 수 있다. 이러한 애플리케이션의 경우 diffusion model을 학습시키기 위해 타겟 콘텐츠의 대규모 데이터셋을 수집할 여유가 없지만 쉽게 사용할 수 있는 더 작은 조각에 대해 학습된 diffusion model로 고품질 타겟 콘텐츠를 합성하고자 한다.

이러한 종류의 문제에 대한 일반적인 해결책은 먼저 콘텐츠의 작은 부분에 대해 diffusion model을 학습시킨 다음 autoregressive 방식으로 큰 콘텐츠를 하나씩 생성하는 것이다. 그러나 이러한 autoregressive 접근 방식에는 세 가지 단점이 있다.

1. 조각이 순차적으로 생성되기 때문에 나중에 생성되는 조각은 이전 생성 조각에 영향을 미치지 않는다. 이러한 순차적 체계는 특히 데이터에 순환 구조가 있는 경우 좋지 못한 결과를 초래할 수 있다.
2. Autoregressive 방법은 모델이 학습 중에는 ground-truth 데이터로 컨디셔닝되었지만 테스트 시에는 자체적인 예측에 따라 컨디셔닝되기 때문에 오차 누적으로 인해 어려움을 겪을 수 있다.
3. Autoregressive 생성에 소요되는 시간은 데이터 크기에 따라 선형적으로 증가하며 매우 큰 콘텐츠를 생성할 때 사용할 수 없다.

본 논문은 대용량 콘텐츠 생성 문제를 해결하기 위해 대용량 콘텐츠의 작은 조각에 대해 학습된 diffusion model에서 생성된 결과를 병합하여 대용량 콘텐츠를 합성하는 알고리즘인 DiffCollage를 제안한다. 본 논문의 접근 방식은 일부 데이터가 일련의 node와 node를 연결하는 edge로 모델링되는 factor graph formulation을 기반으로 한다. 각 node는 큰 콘텐츠의 연속 부분을 나타내며 인접 node의 콘텐츠 부분은 약간 겹친다. 각 node는 작은 diffusion model과 연결되며 각 조각은 다른 조각의 생성에 영향을 미친다. 본 논문의 방법은 병렬로 여러 콘텐츠를 생성하므로 대규모 계산 풀을 사용할 수 있을 때 샘플링을 크게 가속화할 수 있다.

저자들은 무한 이미지 생성, 복잡한 동작이 포함된 long-duration text-to-motion, loop motion과 같은 비정상적인 구조의 콘텐츠, 360도 이미지를 포함한 여러 대규모 콘텐츠 생성 작업에 대한 접근 방식을 평가하였다. 실험 결과는 본 논문의 접근 방식이 기존 접근 방식보다 훨씬 뛰어난 성능을 보인다는 것을 보여준다.

Preliminaries

Diffusion model은 forward diffusion process와 reverse process의 두 가지 과정으로 구성된다. Forward diffusion process는 점진적으로 데이터 분포 $q_0 (u_0)$의 샘플에 Gaussian noise를 주입하고 noisy한 데이터 분포 $q_t (u_t)$를 생성한다. $u_0$으로 컨디셔닝된 $u_t$의 분포도 Gaussian임을 알 수 있다.

\[\begin{equation} q_{0t} (u_t \vert u_0) = \mathcal{N} (u_0, \sigma_t^2 I) \end{equation}\]

표준 편차 $\sigma_t$는 forward diffusion time $t$에 대해 단조 증가한다. Reverse process는 noisy한 데이터에서 반복적으로 denoise하여 깨끗한 데이터를 복구하도록 설계되었으며, 이는 다음과 같은 확률미분방정식(SDE)으로 공식화할 수 있다.

\[\begin{equation} du = - (1 + \eta^2) \dot{\sigma}_t \sigma_t \nabla_u \log q_t (u) dt + \eta \sqrt{2 \dot{\sigma}_t \sigma_t} dw \end{equation}\]

여기서 $\nabla_u \log q_t (u)$는 noise가 추가된 데이터 분포의 score function이며, $w_t$느 standard Wiener process이고 $\eta \ge 0$는 denoising process 중에 주입되는 random noise의 양을 결정한다. $\eta = 1$이면 위의 SDE는 forward diffusion process의 reverse-time SDE가 되고 ancestral sampling과 Euler-Maruyama에 기반한 sampler를 사용할 수 있다. $\eta = 0$이면 위 SDE는 probability flow ODE가 된다. 실제로 score function을 알 수 없기 때문에 신경망 $s_\theta (u, t)$로 추정되며, 다음과 같은 목적 함수를 최소화하여 학습된다.

\[\begin{equation} \underset{\theta}{\arg \min} \mathbb{E}_{t, u_0} [ \omega (t) \| \nabla_{u_t} \log q_{0t} (u_t \vert u_0) - s_\theta (u_t, t) \|^2 ] \end{equation}\]

여기서 $\omega (t)$는 시간에 의존하는 가중치이다.

Diffusion Collage

DiffCollage는 대용량 콘텐츠의 일부로 구성된 데이터에서 학습된 diffusion model을 사용하여 대용량 콘텐츠를 병렬로 생성할 수 있는 알고리즘이다.

1. Representation

A simple example

DiffCollage의 간단한 사용 예시는 짧은 이미지에서 학습된 diffusion model을 조합하여 긴 이미지를 생성하는 것이다. 이 문제에 대한 autoregressive 솔루션은 먼저 초기 정사각형 이미지를 생성한 다음 이전에 생성된 이미지의 일부를 조건으로 outpainting을 수행하여 결과 이미지가 약간 더 커지는 것이다. 이 더 커진 이미지를 $u = [x^{(1)}, x^{(2)}, x^{(3)}]$으로 나타내며, $[x^{(1)}, x^{(2)}]$는 초기 이미지이고 $x^{(3)}$은 조건부 모델 $x^{(3)} \vert x^{(2)}$로 outpainting된 이미지이다. 결합 분포는 다음과 같다.

\[\begin{aligned} q(u) &= q(x^{(1)}, x^{(2)}, x^{(3)}) = q(x^{(1)}, x^{(2)}) q(x^{(3)} \vert x^{(2)}) \\ &= \frac{q(x^{(1)}, x^{(2)}) q(x^{(2)}, x^{(3)})}{ q(x^{(2)})} \end{aligned}\]

$q(u)$의 score function은 더 작은 이미지들의 score의 합으로 표현된다.

\[\begin{aligned} \nabla \log q(u) =& \; \nabla \log q(x^{(1)}, x^{(2)}) + \nabla \log q(x^{(2)}, x^{(3)}) \\ & - \nabla \log q(x^{(2)}) \end{aligned}\]

각 개별 score는 더 작은 이미지에서 학습된 diffusion model을 사용하여 추정할 수 있다. 콘텐츠를 순차적으로 생성하는 autoregressive 방법과 달리 DiffCollage는 모든 개별 score를 독립적으로 계산할 수 있으므로 병렬로 다른 조각을 생성할 수 있다.

Generalization to arbitrary factor graphs

위의 예시를 더 복잡한 시나리오로 일반화하자. 결합 변수 $u = [x^{(1)}, x^{(2)}, \cdots, x^{(n)}]$에 대하여, factor graph는 variable node \(\{x^{(i)}\}_{i=1}^n\)와 factor node \(\{f^{(j)}\}_{j=1}^m\)를 연결하는 이분 그래프(bipartite graph)이고 \(f^{(j)} \subseteq \{x^{(1)}, x^{(2)}, \cdots, x^{(n)}\}\)이다.

$x^{(i)}$와 $f^{(j)}$ 사이의 무방향 edge는 $x^{(i)} \in f^{(j)}$를 의미한다. 위의 예시에서는 2개의 factor \(f^{(1)} = \{x^{(1)}, x^{(2)}\}\)와 \(f^{(2)} = \{x^{(2)}, x^{(3)}\}\)가 있다. $q(u)$의 factorization을 나타내는 factor graph가 주어지면 DiffCollage는 다음과 같이 분포를 근사한다.

\[\begin{equation} p(u) := \frac{\prod_{j=1}^m q(f^{(j)})}{\prod_{i=1}^n q(x^{(i)})^{d_i - 1}} \end{equation}\]

$d_i$는 $x^{(i)}$의 degree이다. $q(u)$의 score는 factor node의 score를 전부 더한 값에 leaf node가 아닌 variable node의 score를 전부 빼서 근사할 수 있다.

\[\begin{equation} \nabla \log p(u) := \sum_{j=1}^m \nabla \log q(f^{(j)}) + \sum_{i=1}^n (d_i - 1) \nabla \log q(x^{(i)}) \end{equation}\]

사실, 위 식은 확률적 그래픽 모델 논문에서 factor node와 variable node에 대해 정의된 주변 분포에 의해 공동 분포 $q(u)$를 근사화하는 중요한 Bethe approximation로 알려져 있다. Factor graph가 비순환 그래프일 때 근사값은 정확하며 $p(u) = q(u)$이다. 순환이 있는 일반 그래프의 경우 Bethe approximation가 실제로 널리 사용되며 좋은 성능을 얻는다.

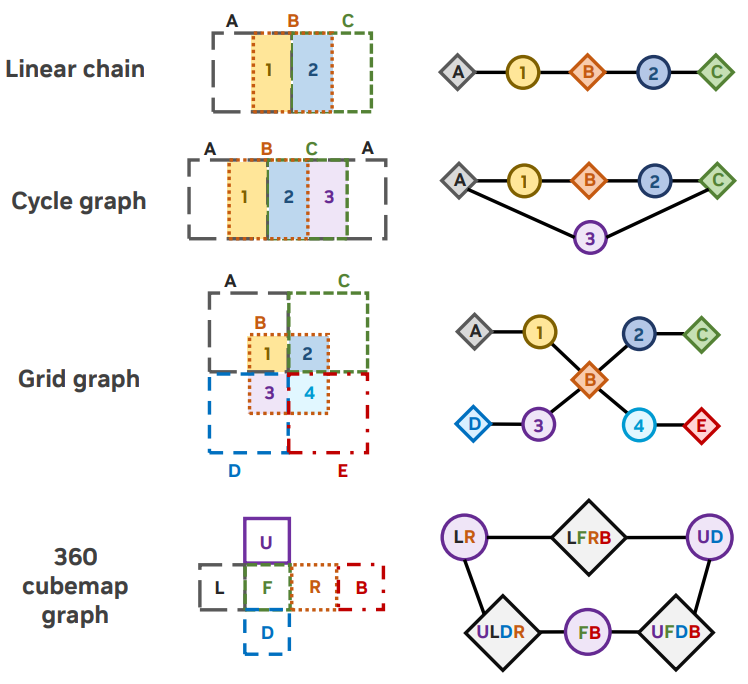
실제로 위 그림과 같이 factor graph는 임의의 크기와 모양의 컨텐츠를 커버하는 데 충분히 일반적이다.

2. Training and Sampling

Training

DiffCollage는 noise가 추가된 데이터 분포 $q_t (u)$의 score를 추정하도록 학습되었다. 깨끗한 데이터에 대한 Bethe approximation과 유사하게 $q_t (u)$의 score를 factorize한다.

\[\begin{aligned} \nabla \log p_\theta (u, t) =& \; \sum_{j=1}^m \nabla \log p_\theta (f^{(j)}, t) \\ & + \sum_{i=1}^n (1 - d_i) \nabla \log p_\theta (x^{(i)}, t) \end{aligned}\]

학습된 모델과 Bethe approximation의 차이를 좁히기 위해 실제 데이터의 score \(\{q(x^{(i)}, t), q(f^{(j)}, t)\}\)와 학습된 score \(\{p_\theta (x^{(i)}, t), p_\theta (f^{(j)}, t)\}\) 사이에서 denoising score matching을 수행하여 $\theta$를 최적화한다. 이는 실제 데이터의 각 주변 분포에 대한 diffusion model을 학습하여 수행할 수 있다.

하나의 결합 분포를 근사화하는 것을 목표로 하지만 하나의 주변 분포에 대한 diffusion model을 학습하는 것은 다른 주변 분포를 학습하는 것과는 독립적이라는 점에 유의해야 한다. 이러한 독립성으로 서로 다른 주변 분포에 대한 diffusion model을 병렬로 학습할 수 있다. 실질적으로, 서로 다른 주변 분포에 대한 diffusion model은 factor node $f^{(j)}$의 조건부 신호 $y$와 variable node $x^{(i)}$의 $y$를 사용하여 하나의 공유 diffusion model을 사용하여 다양한 주변 분포를 학습하는 경우 상각될 수 있다.

Sampling

각 주변 분포에 대한 diffusion model을 학습시킨 후 $p_\theta (u, t)$에 대한 DiffCollage의 score model은 위의 공식으로 간단히 얻을 수 있으며, 특정 score 근사값을 가진 diffusion model이다. 따라서 DiffCollage는 sampler에 구애받지 않으며 기존 solver(ex. DDIM, DEIS, DPM-Solver, gDDIM)를 수정 없이 활용하여 대략적인 score로 샘플을 생성할 수 있다.

기존의 autoregressive 접근 방식과 달리 다양한 주변 분포에 대한 diffusion model을 동시에 평가하고 서로 다른 데이터 \(\{f^{(j)}, x^{(i)}\}\) 조각을 병렬로 생성할 수 있으므로 고급 sampler를 사용하면 DiffCollage에 의한 반복 횟수는 autoregressive 모델보다 훨씬 적을 수 있다.

Experiments

생성된 파라노마 이미지의 생성 품질을 비교하기 위하여 저자들은 FID+를 도입하였다. FID+는 비율이 $W/H = 6$인 5만 개의 파라노마 이미지들을 생성하고 랜덤하게 $H \times H$로 crop한 총 5만 개의 이미지에서 FID를 측정한 것이다.

1. Infinite image generation

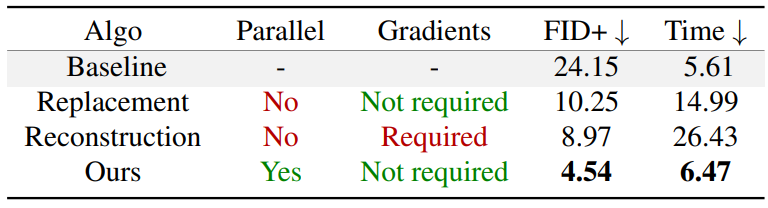
다음은 내부 landscape 데이터셋에서 무한 이미지 생성에 대한 다양한 diffusion 기반 방법을 비교한 표이다.

다음은 다양한 접근 방식으로 생성된 긴 이미지이다.

오차 누적으로 인해 이미지가 커짐에 따라 autoregressive 접근 방식의 샘플 품질이 저하되는 반면, DiffCollage에는 이 문제가 없음을 보여준다.

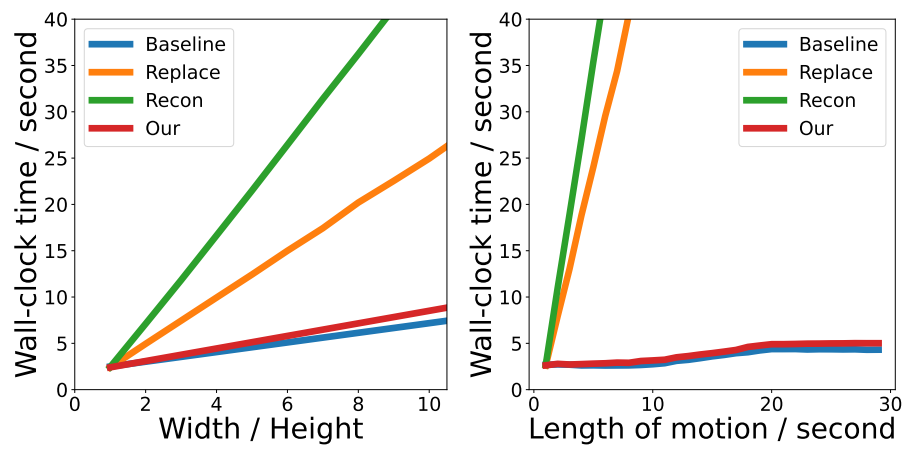
다음은 다양한 이미지 길이(왼쪽)와 모션 시퀀스 길이(오른쪽)에 대하여 생성에 소요되는 시간을 나타낸 그래프이다.

다음은 실제 이미지를 연결한 이미지이다. 64$\times$64 크기의 실제 이미지 $x^{(0)}과 $x^{(n)}$이 주어지면 DiffCollage는 1024$\times$10752 이미지를 생성할 수 있다.

한 스타일에서 완전히 다른 스타일로 전환되는 긴 이미지를 생성할 수 있다.

다음은 무한 이미지 생성을 위해 설계된 다양한 방법을 비교한 표이다.

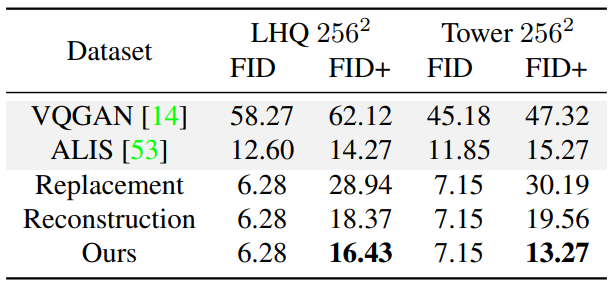
2. Arbitrary-sized image translation

다음은 높이와 너비의 크기가 다른 이미지를 inpainting한 예시이다.

3. Text-to-motion generation

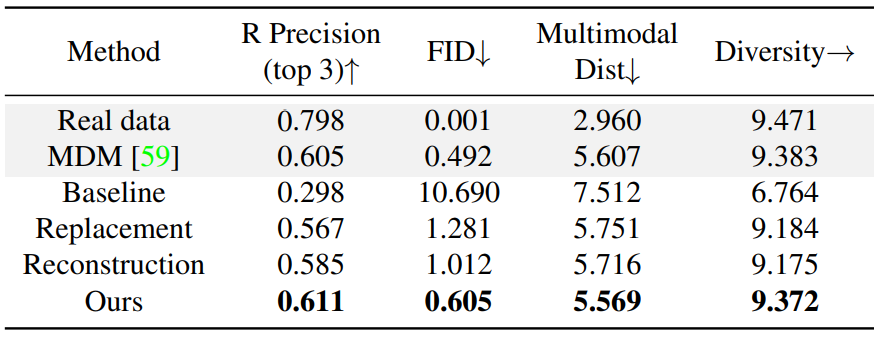
다음은 HumanML3D test set에서 long-duration 생성의 정량적 결과를 나타낸 표이다.

다음은 간단한 모션으로 학습된 diffusion model로 복잡한 모션을 합성한 예시이다.

프롬프트:
(Top) A person runs forward, then kicks his legs, then skips rope, then bends down to pick something up off the ground.
(Bottom) A person runs forward, then skips rope, then bends down to pick something up off the ground, then kicks his legs.

4. Generation with complex graphs

다음은 DiffCollage가 복잡한 그래프로 지정된 어려운 종속성 구조로 데이터를 생성할 수 있음을 보여준다.

위 그림 상단과 같이 DiffCollage는 순환 그래프를 구성하여 수평 파노라마를 생성할 수 있다. 또한 본 논문의 방법을 적용하여 semantic segmentation map(위 그림 하단)에서 조정된 일반 원근 이미지에서만 학습된 diffusion model을 사용하여 360도 파노라마를 생성할 수 있다.