Blogs

arXiv 2022. [Paper]
Andreas Blattmann, Robin Rombach, Kaan Oktay, Jonas Müller, Björn Ommer
LMU Munich, MCML & IWR, Heidelberg University
25 Apr 2022

Introduction

심층 생성 모델링에서 특히 언어 모델링과 고화질 이미지 및 기타 데이터 유형의 생성적 합성은 엄청난 도약을 이루었다. 특히 이미지의 경우 최근 놀라운 성과를 거두고 있으며 이러한 발전의 원동력으로 세 가지 주요 요인을 확인할 수 있다. 첫째, Transformer의 성공은 많은 비전 task에서 아키텍처의 혁명을 일으켰으며, 특히 autoregressive 모델링과 결합하여 사용된다. 둘째, diffusion model은 고해상도 이미지 생성에 적용되었으며 매우 짧은 시간 내에 생성 이미지 모델링의 새로운 표준이 되었다. 셋째, 이러한 접근 방식은 확장성이 좋으며, 특히 고품질 모델과 관련된 모델 및 배치 크기를 고려할 때 이러한 확장성이 성능에 가장 중요하다는 증거다. 그러나 이 학습 패러다임의 기본 원동력은 막대한 계산 리소스를 필요로 하는 파라미터 수가 계속 증가하는 모델이다. 에너지 소비와 학습 시간에 대한 막대한 요구 외에도 이 패러다임은 미래 생성 모델링을 특권 기관에 점점 더 독점적으로 만든다. 따라서 여기서는 새로운 접근 방식을 제시한다.

본 논문은 Retrieval-augmented NLP의 최근 발전에 영감을 받아 서로 다른 학습 예제 간에 공유되는 시각적 개념을 많은 수의 학습 가능한 파라미커로 고가로 압축하는 일반적인 접근 방식에 의문을 제기하고 비교적 작은 생성 모델에 큰 이미지 데이터베이스를 제공한다. 학습하는 동안 결과로 생성되는 semi-parametric generative model은 nearest neighbor lookup을 통해 이 데이터베이스에 액세스하므로 처음부터 데이터를 생성하는 방법을 배울 필요가 없다. 대신 검색된 시각적 인스턴스를 기반으로 새로운 장면을 구성하는 방법을 배운다. 이 방법은 파라미터 수를 줄임으로써 생성 성능을 향상시킬 뿐만 아니라 학습 중에 컴퓨팅 요구 사항을 낮춘다 (위 그림 참고). 본 논문이 제안한 접근 방식은 inference 중에 모델이 사후 모델 수정의 한 형태로 해석될 수 있으며 추가 학습 없이 대체 이미지 데이터베이스의 형태로 새로운 지식으로 일반화할 수 있도록 한다. 학습 후 검색 데이터베이스를 WikiArt 데이터셋으로 대체하여 모델을 zero-shot 스타일화에 적용하여 이를 보여준다.

또한, 본 논문의 접근 방식은 기본 생성 모델과 독립적으로 공식화되어 retrieval-augmented diffusion (RDM)과 autoregressive (RARM) 모델을 모두 제시할 수 있다. CLIP의 latent space를 검색 및 조정하고 NN-search에 scaNN을 사용함으로써 검색은 학습/inference 시간(20M 예제의 데이터베이스에서 가장 가까운 이웃 20개를 검색하는 데 0.95ms) 및 저장 공간(1M당 2GB)에서 무시할 수 있는 오버헤드를 유발한다. Semi-parametric model이 높은 fidelity와 다양한 샘플을 생성한다는 것을 보여준다. RDM은 FID와 다양성 측면에서 최신 diffusion model을 능가하는 동시에 학습 가능한 파라미터가 덜 필요하다. 또한 CLIP의 공유 이미지-텍스트 feature space는 이미지에 대해서만 학습되었음에도 불구하고 text-to-image 또는 클래스 조건부 합성과 같은 다양한 조건부 애플리케이션이 가능하다. 마지막으로, diffusion model을 위한 classifier-free guidance 또는 autoregressive model을 위한 top-k 샘플링과 같은 모델별 샘플링 기술과 결합할 수 있는 합성 프로세스를 제어하기 위한 추가적인 truncation 전략을 제시한다.

Image Synthesis with Retrieval-Augmented Generative Models

본 논문은 데이터 포인트를 모델의 명시적인 부분으로 간주한다. 이미지 합성을 위한 일반적인 생성적 접근 방식과 달리 이 접근 방식은 신경망의 학습 가능한 가중치에 의해 parameterize될 뿐만 아니라 고정된 데이터 표현 셋과 학습 불가능한 검색 함수로, 학습 데이터는 외부 데이터셋에서 적절한 데이터 표현을 검색한다. 자연어 모델링의 이전 연구에 이어 이 검색 파이프라인을 nearest neighbor lookup으로 구현한다.

1. Retrieval-Enhanced Generative Models of Images

이미지에 대한 일반적이고 완전한 parametric 생성적 접근 방식과 달리 학습 가능한 파라미터 $\theta$와 학습 불가능한 모델 구성요소 $\mathcal{D}$, $\xi_k$를 도입하여 semi-parametric 생성적 이미지 모델 $p_{\theta, \mathcal{D}, \xi_k} (x)$를 정의한다. 여기서 \(\mathcal{D} = \{y_i\}_{i=1}^N\)는 학습 데이터 $X$와 분리된 이미지 $y_i \in \mathbb{R}^{H_\mathcal{D} \times W_\mathcal{D} \times 3}$의 고정 데이터베이스이다. 또한, $\xi_k$는 쿼리 $x$에 기반하여 $\mathcal{D}$의 부분집합을 얻기 위한 학습 불가능한 샘플링 전략을 나타낸다.

\[\begin{equation} \xi_k: x, \mathcal{D} \mapsto \mathcal{M}_\mathcal{D}^{(k)} \\ \textrm{where} \quad \mathcal{M}_\mathcal{D}^{(k)} \subseteq \mathcal{D}, \quad | \mathcal{M}_\mathcal{D}^{(k)} | = k \end{equation}\]

따라서 학습 중에 실제로는 $\theta$만 학습된다.

중요한 것은 $\xi_k (x, \mathcal{D})$를 선택하여 $x$ 모델링을 위한 $\mathcal{D}$의 유익한 시각적 표현을 모델에 제공하고 $\theta$의 전체 용량을 활용하여 이러한 패턴을 기반으로 일관된 장면을 구성할 수 있다는 것이다. 예를 들어, 쿼리 이미지 $x \in \mathbb{R}^{H_x \times W_x \times 3}$을 고려할 때 유효한 전략 $\xi_k (x, \mathcal{D})$는 각 $x$에 대해 주어진 거리 함수 $d(x, \cdot)$로 측정한 $k$개의 nearest neighbors의 집합을 return한다.

다음으로, 컨디셔닝을 통해 이 검색된 정보를 모델에 제공한다. 즉, 일반적인 semi-parametric generative model을 다음과 같이 쓸 수 있다.

\[\begin{equation} p_{\theta, \mathcal{D}, \xi_k} (x) = p_\theta (x \; \vert \; \xi_k (x, \mathcal{D})) = p_\theta (x \; \vert \; \mathcal{M}_\mathcal{D}^{(k)}) \end{equation}\]

원칙적으로 이미지 샘플 \(y \in \mathcal{M}_\mathcal{D}^{(k)}\)를 직접 사용하여 $\theta$를 학습할 수 있다. 그러나 이미지에는 많은 모호성이 포함되어 있고 높은 차원에는 상당한 계산 및 저장 비용이 포함되기 때문에 고정된 사전 학습된 이미지 인코더 $\phi$를 사용하여 $\mathcal{M}_\mathcal{D}^{(k)}$의 모든 예를 저차원 manifold에 project한다. 따라서 위 식은 다음과 같이 다시 쓸 수 있다.

\[\begin{equation} p_{\theta, \mathcal{D}, \xi_k (x)} = p_\theta (x \; \vert \; \{ \; \phi(y) \; \vert \; y \in \xi_k (x, \mathcal{D}) \; \}) \end{equation}\]

여기서 $p_\theta (x \vert \cdot)$은 학습 가능한 파라미터 $\theta$를 가지는 조건부 생성 모델이며 decoding head라고 부른다. 이를 통해 위의 절차는 모든 유형의 생성 decoding head에 적용될 수 있으며 구체적인 학습 절차에 의존하지 않는다.

2. Instances of Semi-Parametric Generative Image Models

학습하는 동안 분포 $p(x)$를 $p_{\theta, \mathcal{D}, \xi_k (x)}$로 근사하려는 이미지의 학습 데이터셋 \(X = \{x_i\}_{i=1}^M\)이 제공된다. 학습 시간 샘플링 전략 $\xi_k$는 쿼리 예제 $x \sim p(x)$를 사용하여 CLIP의 이미지 feature space 공간에서 $d(x, y)$를 코사인 유사성으로 구현하여 $k$개의 nearest neighbor $y \in \mathcal{D}$를 검색한다. 충분히 큰 데이터베이스 $\mathcal{D}$가 주어지면 이 전략은 neighbor의 집합 $\xi_k(x, \mathcal{D})$가 $x$와 충분한 정보를 공유하고 따라서 생성 task에 유용한 시각적 정보를 제공하도록 보장한다. 저차원 space (dim = 512)에 이미지를 삽입하고 의미론적으로 유사한 샘플을 동일한 neighbor에 매핑하여 효율적인 검색 space를 생성하기 때문에 $\xi_k$를 구현하기 위해 CLIP을 선택한다. 아래 그림은 ViT-B/32 Vision Transformer backbone을 통해 검색된 nearest neighbor의 예를 시각화한 것이다.

이 접근 방식은 원칙적으로 모든 생성 모델을 semi-parametric model로 전환할 수 있다. 본 논문에서는 decoding head가 이미지 합성에서 성공한 모델인 diffusion model과 autoregressive model로 구현되는 모델에 초점을 맞춘다.

$\phi$를 통해 이미지 표현을 얻기 위해 원칙적으로 다른 인코딩 모델을 생각할 수 있다. 다시 말하지만, CLIP의 latent space는 매우 작기 때문에 메모리 요구 사항도 감소하므로 몇 가지 이점을 제공한다. 또한 대조적인 사전 학습 목적 함수는 이미지와 텍스트 표현의 공유 space를 제공하며, 이는 텍스트-이미지 합성에 유리하다.

이 선택으로 추가 데이터베이스 $\mathcal{D}$는 nearest neighbor이 검색되는 차원 $\vert \mathcal{D} \vert \times 512$의 고정 임베딩 레이어로 해석될 수도 있다.

Retrieval-Augmented Diffusion Models

학습 중 계산 복잡성과 메모리 요구 사항을 줄이기 위해 사전 학습된 오토인코더의 latent space $z = E(x)$에서 데이터 분포를 학습하는 latent diffusion model (LDM)을 따르고 구축한다. 저자들은 이 retrieval-augmented latent diffusion model을 RDM이라고 명명하고 일반적인 재가중 목적 함수로 학습시킨다.

\[\begin{equation} \min_\theta \mathcal{L} = \mathbb{E}_{p(x), z \sim E(x), \epsilon \sim \mathcal{N}(0,1), t} [\| \epsilon - \epsilon_\theta (z_t, t, \{\phi_\textrm{CLIP} (y) \; \vert \; y \in \xi_k (x, \mathcal{D})\}) \|_2^2] \end{equation}\]

위의 식에서 $\theta$는 UNet 기반 denoising autoencoder를 나타내며 \(t \sim \textrm{Uniform} \{1, \cdots, T\}\)는 timestep을 나타낸다. Nearest neighbor 인코딩의 집합 $\phi_\textrm{CLIP} (y)$를 $\theta$에 공급하기 위해 cross-attenton mechanism을 사용한다.

Retrieval-Augmented Autoregressive Models

본 논문의 접근 방식은 여러 유형의 likelihood 기반 방법에 적용할 수 있다. 저자들은 검색된 표현을 사용하여 diffusion model과 autoregressive model을 augment하여 이를 보여준다. 후자를 구현하기 위해 VQGAN의 이산적인 이미지 토큰 $z_q = E(x)$의 분포를 모델링하기 위해 autoregressive transformer model을 학습시킨다. 구체적으로, RDM과 비슷하게 $\phi_\textrm{CLIP} (y)$로 컨디셔닝한 retrieval-augmented autoregressive model (RARM)을 학습시킨다. 목적 함수는 다음과 같다.

\[\begin{equation} \min_\theta \mathcal{L} = -\mathbb{E}_{p(x), z_q \sim E(x)} \bigg[\sum_i \log p(z_q^{(i)} \; \vert \; z_q^{(< i)}, \; \{\phi_\textrm{CLIP} (y) \; \vert \; y \in \xi_k (x, \mathcal{D}) \}) \bigg] \end{equation}\]

여기서 latent $z_q$의 autoregressive factorization을 위해 row-major ordering을 선택한다. Cross-attenton을 통해 neighbor 임베딩의 집합 $\phi_\textrm{CLIP} (\xi_k(x, \mathcal{D}))$로 모델을 컨디셔닝한다.

3. Inference for Retrieval-Augmented Generative Models

Conditional Synthesis without Conditional Training

테스트 시에 학습되지 않은 $\mathcal{D}$와 $\xi_k$를 변경할 수 있다는 것은 표준 생성 접근 방식에 비해 추가적인 유연성을 제공한다. 애플리케이션에 따라 특정 예시에 대해 $\mathcal{D}$를 확장/제한할 수 있다. 또는 $\xi_k$를 통한 검색을 모두 건너뛰고 일련의 표현 \(\{\phi_\textrm{CLIP}(y_i)\}_{i=1}^k\)을 직접 제공할 수 있다. 이를 통해 학습 중에는 사용할 수 없었던 텍스트 프롬프트 또는 클래스 레이블과 같은 추가 조건부 정보를 사용하여 합성 중에 보다 세분화된 제어가 가능하다.

Text-to-image generation

Text-to-image 생성의 경우, 예를 들어 모델은 여러 가지 방법으로 컨디셔닝 될 수 있다. 텍스트 프롬프트 $c_\textrm{text}$가 주어지고 CLIP의 text-to-image 검색 능력을 사용하여 $\mathcal{D}$에서 $k$개의 neighbor을 검색하고 이를 텍스트 기반 컨디셔닝으로 사용할 수 있다. 그러나 CLIP 표현 $\phi_\textrm{CLIP}$에 대해 컨디셔닝하기 때문에 CLIP의 언어 backbone을 통해 얻은 텍스트 임베딩으로 직접 컨디셔닝할 수도 있다 (CLIP의 텍스트-이미지 임베딩 space가 공유되기 때문에). 따라서 이러한 접근 방식을 결합하고 텍스트와 이미지 표현을 동시에 사용할 수도 있다.

클래스 레이블 $c$가 주어지면 텍스트 설명 $t(c)$를 기반으로 ‘An image of a $t(c)$.’와 같은 텍스트를 정의하거나 텍스트 프롬프트에 임베딩 전략을 적용하고 각 클래스에 대한 pool $\xi_l(c), k ≤ l$을 샘플링한다. 주어진 쿼리 $c$에 대해 이 pool에서 $k$개의 neighbor 예제를 임의로 선택하여 inference-time 클래스 조건 모델을 얻는다.

Unconditional generative modeling

Unconditional generative modeling의 경우, pseudo-query $\tilde{x} \in \mathcal{D}$를 랜덤하게 샘플링하여 $k$개의 nearest neighbor의 집합 $\xi_k^\textrm{test} (\tilde{x}, \mathcal{D})$를 얻는다. 이 집합이 주어지면 $p_\theta (x \vert \cdot)$ 자체가 생성 모델이기 때문에 샘플을 그리는 데 사용할 수 있다. 그러나 $p_\theta, \mathcal{D}, \xi_k(x)$에서 모든 샘플을 하나의 특정 집합 $\xi_k^\textrm{test} (\tilde{x})$에서만 생성할 때 $p_\theta, \mathcal{D}, \xi_k(x)$가 unimodal이고 $\tilde{x}$ 주변에서 급격하게 피크가 될 것으로 기대한다. 자연 이미지의 복잡한 multimodal 분포 $p(x)$를 모델링하려고 할 때 이 선택은 분명히 약한 결과를 초래할 것이다. 따라서 $\mathcal{D}$를 기반으로 다음과 같은 분포를 구성한다.

\[\begin{equation} p_\mathcal{D} (\tilde{x}) = \frac{|\{x \in \mathcal{X} \; \vert \; \tilde{x} \in \xi_k (x, \mathcal{D})\}|}{k \cdot |\mathcal{X}|}, \quad \textrm{for } \tilde{x} \in \mathcal{D} \end{equation}\]

이 정의는 학습 데이터셋 $\mathcal{X}$를 모델링하는 데 유용한 데이터베이스 $\mathcal{D}$의 인스턴스 수를 계산한다. $p_\mathcal{D} (\tilde{x})$는 $\mathcal{X}$와 $\mathcal{D}$에만 의존하므로 미리 계산할 수 있다. 주어진 $p_\mathcal{D} (\tilde{x})$에 대하여 모델에서 다음과 같은 샘플의 집합을 얻을 수 있다.

\[\begin{equation} \mathcal{P} = \bigg\{ x \sim p_\theta (x \; \vert \; \{\; \phi(y) \; \vert \; y \in \xi_k (\tilde{x}, \mathcal{D}) \;\}) \; \vert \; \tilde{x} \sim p_\mathcal{D} (\tilde{x}) \bigg\} \end{equation}\]

따라서 $x \sim \textrm{Uniform}(\mathcal{P})$를 사용하여 unconditional한 모델링된 밀도 $p_{\theta, \mathcal{D}, \xi_k (x)}$에서 샘플링할 수 있다.

가장 가능성이 높은 예시 $\tilde{x} \sim p_\mathcal{D}(\tilde{x})$에서 $m \in (0, 1]$만큼 선택하여 이 분포를 인위적으로 자르고 다양성을 위해 샘플 품질을 교환할 수 있다.

Experiments

Nearest neighbor을 얻기 위해 ScaNN search algorithm을 사전 학습된 CLIP-ViT-B/32의 feature space에 적용한다. 데이터베이스에서 20개의 nearest neighbor을 검색하며, 0.95ms가 걸린다고 한다. Diffusion model의 경우 100 step의 DDIM sampler ($\eta = 1$)을 사용하여 샘플을 생성한다.

1. Semi-Parametric Image Generation

Finding a train-time database \(\mathcal{D}_\textrm{train}\)

Semi-parametric model의 성공적인 애플리케이션의 핵심은 적절한 학습 데이터베이스 \(\mathcal{D}_\textrm{train}\)을 선택하는 것이다. 이는 학습 데이터베이스가 backbone $p_\theta$에 유용한 정보를 제공하기 때문이다. 저자들은 다양한 시각적 인스턴스가 있는 대규모 데이터베이스가 모델에 가장 유용하다고 가정한다. 이는 모든 학습 예시에 대해 \(\mathcal{D}_\textrm{train}\)에서 nearest neighbor을 찾을 확률이 이 선택에 대해 가장 높기 때문이다. 이 주장을 증명하기 위해 저자들은 다음 3가지 \(\mathcal{D}_\textrm{train}\)과 함께 ImageNet의 개 부분집합 $\mathcal{X}$에서 학습한 3가지 RDM의 시각적 품질과 샘플 다양성을 비교하였다. \(\mathcal{D}_\textrm{train} \cap \mathcal{X} = \emptyset\)이다.

1. WikiArt (RDM-WA)
2. MS-COCO (RDM-COCO)
3. OpenImages의 example 2천만 개 (RDM-OI)

결과는 아래 그래프와 같다.

위 그래프에서 3가지를 알 수 있다.

1. 학습 셋 $\mathcal{X}$보다 다양한 도메인의 예시를 포함한 \(\mathcal{D}_\textrm{train}\)은 샘플 품질을 저하시킨다.
2. $\mathcal{X}$와 같은 도메인의 작은 데이터베이스는 LDM baseline과 비교했을 때 성능이 개선된다.
3. \(\mathcal{D}_\textrm{train}\)의 크기를 키우면 품질과 다양성 모두 향상된다.

\(\mathcal{D}_\textrm{train} \cap \mathcal{X} = \emptyset\)의 이점을 확인하기 위해 ImageNet을 $\mathcal{X}$와 \(\mathcal{D}_\textrm{train}\)으로 모두 사용한 RDM-IN을 학습시켰다. RDM-OI와 RDM-IN의 비교 결과는 다음과 같다.

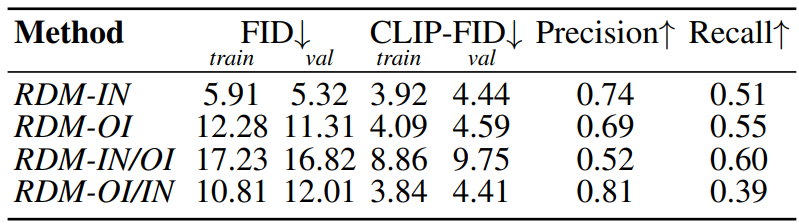
RDM-OI가 RDM-IN와 가까운 CLIP-FID를 달성하는 것을 볼 수 있다. RDM-OI/IN은 RDM-OI를 ImageNet의 예시들로 컨디셔닝한 것이고, RDM-IN/OI는 반대의 경우이다. RDM-OI/IN가 RDM-IN/OI보다 성능이 좋은 것을 볼 수 있으며, RDM-OI/IN의 CLIP-FID가 RDM-IN보다 우수하다는 것을 알 수 있다. 이를 통해 \(\mathcal{D}_\textrm{train} \cap \mathcal{X} = \emptyset\)으로 선택하면 일반화 능력이 향상된다는 것을 알 수 있다.

이 속성의 추가 근거를 제공하기 위해 저자들은 COCO 데이터셋에서 zero-shot text-to-image 합성을 비교하였으며, 그 결과는 아래 표와 같다.

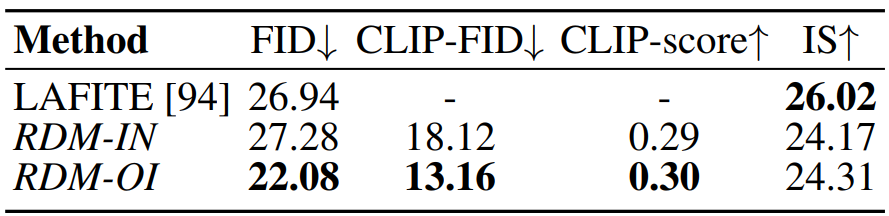
RDM-OI가 FID와 CLIP-score 모두 LAFITE보다 우수하다.

How many neighbors to retrieve during training?

학습 중에 검색되는 nearest neighbor의 개수 $k_\textrm{train}$이 학습 후의 결과 모델의 속성에 큰 영향을 주기 때문에, 최적의 합성 속성을 가지는 모델이 되기 위한 hyperparameter를 선택해야 한다. 따라서 저자들은 $p_\theta$를 diffusion model로 parameterize하고 ImageNet에서 \(k_\textrm{train} \in \{1, 2, 4, 8, 16\}\)에 대하여 5개의 모델을 학습시켰다. 모든 모델들은 동일한 backbone과 계산 리소스를 사용한다.

다음은 1000개의 샘플들에 대하여 측정한 FID, IS와 Recall, Precision을 나타낸 그래프이다.

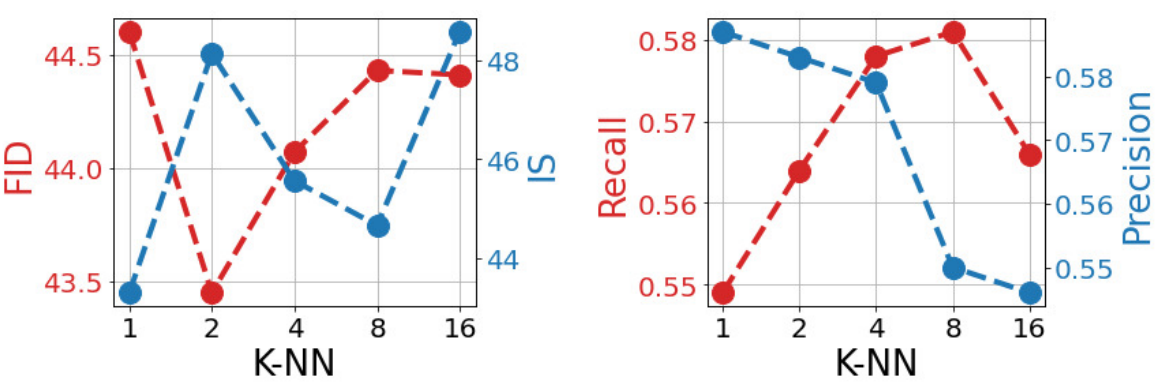
FID와 IS는 중요한 경향을 보이지 않는다. 반면에 Recall과 Precision을 보면, $k_\textrm{train}$을 증가시키면 일관성을 다양성과 맞바꾼다는 것을 알 수 있다. $k_\textrm{train}$이 크면 Recall, 즉 샘플 다양성이 다시 악화된다.

저자들은 이것이 $k_\textrm{train} > 1$일 때 학습 중에 각 모델에 공급되는 하나의 nearest neighbor을 넘어서는 중복되지 않는 추가 정보의 정규화 영향 때문이라고 생각한다. \(k_\textrm{train} \in \{2, 4, 8\}\)의 경우 이 추가 정보가 유익하며 해당 모델은 품질과 다양성 사이를 적절하게 중재한다. 따라서 기본 RDM에 $k = 4$를 사용한다. 또한 neighbor의 수는 조건부 합성 모델의 일반화 능력에 상당한 영향을 미친다.

Qualitative results

위 그림은 주어진 pseudo-query $\tilde{x} \sim p_\mathcal{D} (\tilde{x})$에 대하여 검색된 neighbor의 서로 다른 집합 $\mathcal{M}_\mathcal{D}^{(k)} (\tilde{x})$에 대한 FFHQ의 RDM 샘플뿐만 아니라 ImageNet에서 학습된 RDM과 RARM의 샘플을 보여준다. 또한 저자들은 이 집합이 데이터베이스 $\mathcal{D}$와 분리되어 있고 모델이 보지 못한 새로운 샘플을 렌더링한다는 것을 보여주기 위해 학습 셋에서 nearest neighbor을 plot하였다.

Quantitative results

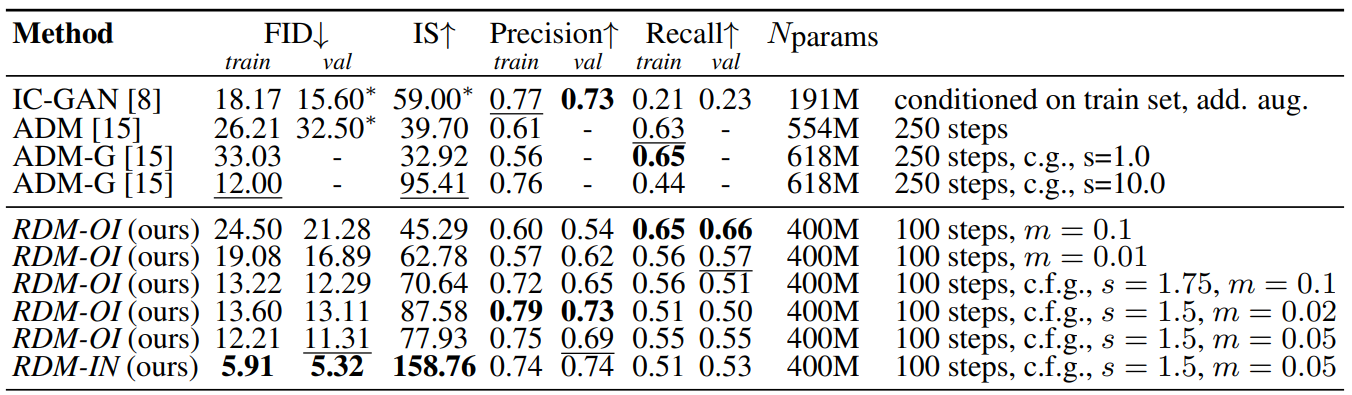
위 표는 본 논문의 모델을 ImageNet 256$\times$256의 unconditional한 이미지 합성에서 최근 state-of-the-art diffusion model ADM과 semi-parametric GAN 기반 모델 IC-GAN(inference 중에 학습 셋 예제에 대한 액세스가 필요)과 비교한다. $s$는 classifier-free guidance (c.f.g.)의 scale parameter이다.

성능을 향상시키기 위해 앞서 설명한 샘플링 전략을 사용한다. Classifier-free guidance를 통해 본 논문의 모델은 ADM-G와 동등하면서 IC-GAN와 ADM보다 더 나은 점수를 얻는다. 학습 데이터에 대한 추가 정보 (ex. 이미지 레이블)가 없으면 RDM은 최상의 전체 성능을 달성한다.

또한 저자들은 FFHQ에서 ImageNet RDM-OI의 복제본을 학습시켰으며, 결과는 아래 표와 같다.

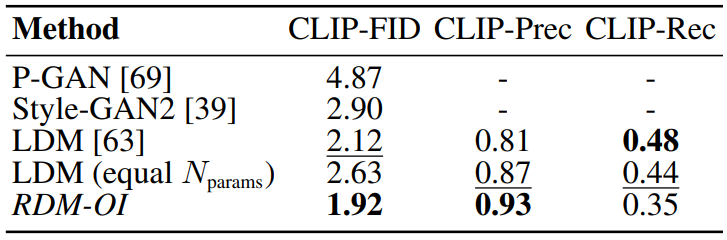
FID는 “얼굴 영역에 둔감”한 것으로 나타났기 때문에 CLIP 기반 metric을 다시 사용한다. FFHQ가 간단한 데이터셋임에도 검색 기반 전략은 다양성(Recall)이 낮아지긴 하지만 강력한 GAN과 diffusion baseline을 능가하는 것으로 입증되었다.

2. Conditional Synthesis without Conditional Training

Text-to-Image Synthesis

위 그림은 사용자가 정의한 텍스트 프롬프트에 대하여 본 논문의 ImageNet model의 zero-shot text-to-image 합성 능력을 보여준다.

실제 텍스트 설명 자체의 CLIP 인코딩 $\phi_\textrm{CLIP} (c_\textrm{text})$를 직접 사용하여 \(\mathcal{M}_\mathcal{D}^{(k)} (c_\textrm{text})\)를 구축할 때 (상단 행) 흥미롭게도 모델이 허구의 설명을 생성하는 것으로 일반화되고 객체 클래스 간에 속성을 전송하는 것을 볼 수 있다. 반면, $\phi_\textrm{CLIP} (c_\textrm{text})$를 데이터베이스 $\mathcal{D}$에서 $k - 1$개의 nearest neighbor과 함께 사용할 때 (중간 행) 모델은 이러한 어려운 조건부 입력으로 일반화되지 않는다. $k$개의 nearest neighbor의 CLIP 이미지 표현만 사용하는 경우 (하단 행) 결과는 더욱 나빠진다.

다음은 학습 중에 $k_\textrm{train}$의 neighbor을 검색하는 것이 RDM의 일반화 능력에 주는 영향을 나타낸 그래프이다.

작은 $k_\textrm{train}$은 해당 모델이 inference 중에 받은 텍스트 표현과 학습된 이미지 표현 사이의 불일치를 처리할 수 없기 때문에 약한 일반화 속성으로 이어진다. $k_\textrm{train}$을 늘리면 \(\mathcal{M}_\mathcal{D}^{(k)} (x)\)가 더 큰 feature space 볼륨을 커버하고 해당 모델을 이러한 불일치에 대해 더 견고하게 정규화한다. 결과적으로 일반화 능력은 $k_\textrm{train}$과 함께 증가하고 $k_\textrm{train} = 8$에서 최적에 도달한다. $k_\textrm{train}$이 더 증가하면 검색된 neighbor을 통해 제공되는 정보가 감소하고 일반화 능력이 저하된다.

다음은 text-to-image 합성 샘플들이다.

Class-Conditional Synthesis

다음은 ImageNet에서의 zero-shot 클래스 조건부 합성에 대한 샘플들이다.

3. Zero-Shot Text-Guided Stylization by Exchanging the Database

Semi-parametric model에서 검색 데이터베이스 $\mathcal{D}$는 합성 모델의 명시적인 부분이다. 이를 통해 학습 후 이 데이터베이스를 교체하여 모델과 그 출력을 수정하는 것과 같은 새로운 애플리케이션이 가능하다.

다음은 ImageNet-RDM의 \(\mathcal{D}_\textrm{train}\)을 WikiArt 데이터셋의 모든 이미지로 구성된 $\mathcal{D}\textrm{style}$로 교체하여 zero-shot text-guided stylization을 수행한 샘플들이다. 하단 행은 $ $\mathcal{D}\textrm{train}$$을 사용하여 동일한 절차로 얻은 샘플을 보여준다.

본 논문의 모델은 ImageNet에서만 학습되었지만 새로운 데이터베이스로 일반화되고 텍스트 프롬프트에 의해 정의된 콘텐츠를 묘사하는 예술 작품과 같은 이미지를 생성할 수 있다.

4. Increasing Dataset Complexity

저자들은 복잡한 생성 task에 대한 다재다능함을 조사하기 위해 학습 데이터 $p(x)$의 복잡성을 체계적으로 증가시킬 때 semi-parametric model을 fully-parametric model과 비교하였다. 저자들은 RDM과 RARM 모두에 대해 ImageNet의 개, 포유류 및 동물 부분 집합에 대해 3개의 동일한 모델과 대응되는 fully-parametric baseline을 학습시켰다. 그 결과는 아래 그래프와 같다.

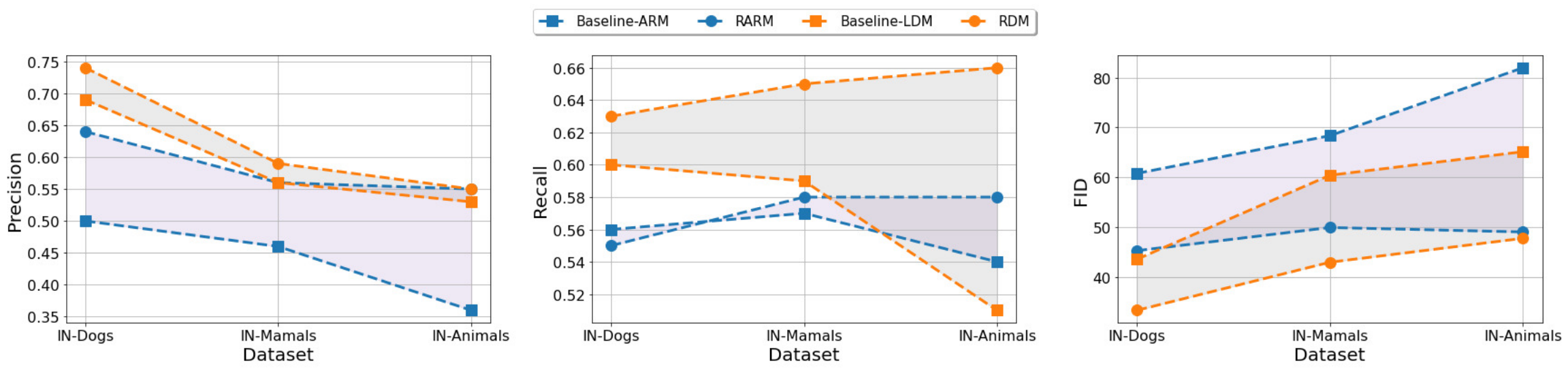
IN-Dogs와 같이 복잡도가 낮은 데이터셋의 경우에도 본 논문의 semi-parametric model은 표준 AR 모델보다 약간 떨어지는 Recall을 제외하고 baseline보다 향상된다. 보다 복잡한 데이터셋의 경우 성능 향상이 더욱 중요해진다. 흥미롭게도 본 논문의 모델의 Recall 점수는 복잡성이 증가함에 따라 향상되는 반면 baseline의 Recall 점수는 크게 저하된다. 저자들은 이것이 $p_\mathcal{D}(\tilde{x})$를 통해 과소 표현된 클래스를 포함하여 모든 클래스에 대한 근처의 시각적 인스턴스에 대한 semi-parametric model의 명시적 액세스에 기인한다고 생각한다. 반면 표준 생성 모델은 가장 자주 발생하는 클래스를 포함하는 모드에만 집중할 수 있다.

5. Quality-Diversity Trade-Offs

다음은 top-m sampling(왼쪽)과 classifier-free guidance(오른쪽)을 사용할 때의 품질-다양성 trade-off를 시각화한 그래프이다.

작은 $m$ 값의 경우 큰 precision 점수로 표시되는 것처럼 모두 단일 또는 소수의 모드에서 오는 일관된 샘플을 얻는다. 반면에 $m$을 늘리면 일관성을 희생시키면서 다양성을 높일 수 있다. FID와 IS의 경우 $m = 0.01$에서 두 지표 모두에 대해 최적의 결과를 보인다.