Blogs

arXiv 2022. [Paper]
Hongyi Yuan, Zheng Yuan, Chuanqi Tan, Fei Huang, Songfang Huang
Tsinghua University | Alibaba Group
20 Dec 2022

Introduction

생성 모델링은 diffusion model의 개발로 인해 최근 몇 년간 기계 학습 연구에서 집중된 영역 중 하나이다. 확산 모델은 GAN 또는 normalizing flow과 같은 다른 생성 방법보다 이미지, 오디오, 동영싱을 합성하는 데 우수한 성능을 보여 왔다.

Diffusion model을 자연어 생성으로 확장하는 것은 쉬운 일이 아니다. 기존 diffusion model의 대부분은 연속적인 feature space에 적용되는 반면 텍스트는 개별 카테고리 토큰의 시퀀스이다. 최근 연구에서는 텍스트 생성을 위해 discrete space에서 카테고리형 diffusion model을 탐색했다. 단어 임베딩에 연속적인 diffusion model을 적용한 DiffusionLM과 같은 연구도 있다. 그러나 이러한 연구들은 unconditional하고 제어된 텍스트 생성에만 중점을 둔다.

본 논문에서는 sequence-to-sequence 텍스트 생성에 중점을 둔다. Sequence-to-sequence 생성은 기본 자연어 처리 세팅이며 대화, 기계 번역, 질문 생성과 같은 다양한 실제 downstream task를 다룬다. 최근에 연구자들은 autoregreesive (AR) 또는 non-autoregreesive Transformers에 의존하며 이러한 방법은 우수한 텍스트 생성 성능을 달성할 수 있다. Sequence-to-sequence 텍스트 생성을 위해 diffusion model을 적용한 DiffuSeq라는 최근 연구도 있다. DiffuSeq에서는 diffusion process를 정의하고 denoising function을 학습하기 위해 부분 noising이 있는 인코더 전용 트랜스포머를 사용한다.

또는 sequence-to-sequence 생성을 위해 인코더-디코더 트랜스포머 아키텍처를 사용한 diffusion model을 탐색한다. 인코더-디코더 아키텍처는 텍스트를 모델링하는 보다 유연한 방법일 수 있다. 본 논문은 DiffusionLM에서 제안한 연속적인 diffusion 프레임워크를 sequence-to-sequence task로 확장한 SeqDiffuSeq를 제안한다. 저자들은 SeqDiffuSeq에 self-conditioning 테크닉을 장착했다. Diffusion model의 경우 적절한 noise schedule이 잠재적으로 생성된 샘플 품질과 likelihood 모델링을 향상시킬 수 있다. 따라서 텍스트 생성을 위한 토큰 레벨의 noise schedule을 학습하는 기법도 제안한다.

Approach

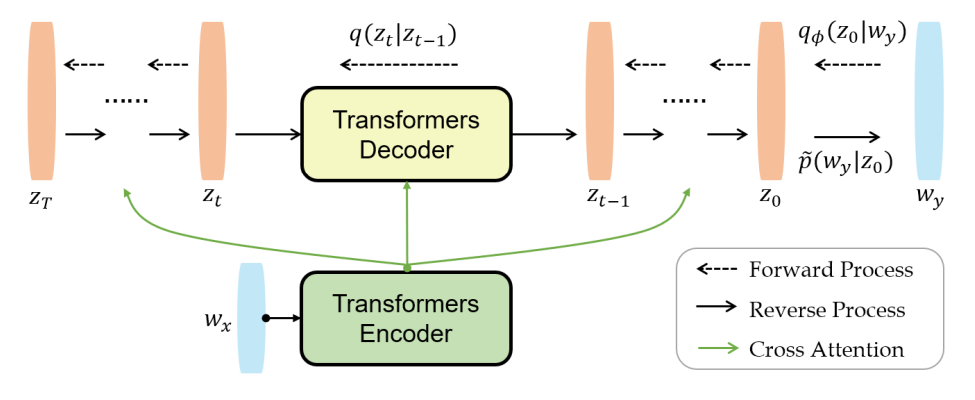
SeqDiffuSeq의 개요는 위 그림에 묘사되어 있다. 입력 및 출력 시퀀스는 각각 $w_x$와 $w_y$로 표시된다. $w_x$ 또는 $w_y$의 $i$번째 토큰의 경우 $w_x^i$ 또는 $w_y^i$로 표시한다. 길이 표기를 피하기 위해 데이터 샘플을 나타내는 인덱스를 생략한다.

1. Diffusion Model

The forward process

본 논문은 iDDPM을 자연어 도메인에 적용한 DiffusionLM에서 제안된 forward process 디자인을 따른다. 출력 시퀀스 $w_y$의 경우 embedding function $g_\phi$를 사용하여 이산적인 단어 토큰 $w_y^i$를 연속적인 단어 임베딩 $g_\phi(w_y^i)$로 매핑한다. 그런 다음 토큰 임베딩을 스택하여 시퀀스 $y$를 위한 임베딩 $g_\phi (w_y) \in \mathbb{R}^{n \times d}$를 정의한다 ($d$는 임베딩의 차원, $n$은 시퀀스 길이). Markov transition이 forward process에 더해지며

\[\begin{equation} q_\phi (z_0 \vert w_y) = \mathcal{N} (z_0; g_\phi (w_y), \beta_0 I) \end{equation}\]

로 parameterize된다. 이 확장된 forward process를 이용하면 이산적인 텍스트의 생성을 기존 연속적인 diffusion model의 forward process로 피팅할 수 있다. 각 timestep에서 diffusion 분포 $q(z_t \vert z_{t-1})$을 사용하여 noise가 점진적으로 더해져 간단한 prior $z_T$를 얻을 수 있다.

The reverse process

Diffusion model의 목적 함수는 주어진 forward diffusion process에 대한 reverse denoising process를 학습하도록 한다. Sequence=to-sequence task의 경우 출력 시퀀스의 생성은 입력 시퀀스를 기반으로 하며, 출력 시퀀스를 직접 diffuse하는 것이 입력 시퀀스에 독립적인 것과 달리 denoising 분포를 학습하는 것은 입력 시퀀스를 기반으로 한다. 따라서 각 timestep에서 reverse process는 parametric 분포 $p_\theta (z_{t-1} \vert z_t, w_x)$를 적용하여 이전 denoising step의 feature뿐만 아니라 입력 시퀀스 $w_x$로도 컨디셔닝한다.

$p_\theta (z_{t-1} \vert z_t, w_x)$가 가우시안 분포 계열인 forward process의 실제 사후 확률 분포 $q(z_{t-1} \vert z_t, z_0)$를 모델링하기 때문에 $p_\theta (z_{t-1} \vert z_t, w_x)$도 가우시안 분포로 공식화할 수 있다.

\[\begin{equation} p_\theta (z_{t-1} \vert z_t, w_x) = \mathcal{N} (z_t; \mu_\theta (z_t, w_x, t), \tilde{\beta}_t I) \\ \mu_\theta (z_t, w_x, t) = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} z_\theta^0 (z_t, w_x, t) + \frac{\sqrt{\alpha_t (1 - \bar{\alpha}_{t-1})}}{1-\bar{\alpha}_t} z_t \end{equation}\]

\(\mathbb{E}_{q(w_x, w_y)} [p_\theta (w_y \vert w_x)]\)의 log-likelihood의 variational bound를 최소화하여 $\theta$를 최적화한다.

\[\begin{aligned} \mathcal{L}_{VB} = \mathbb{E}_{q_\phi (z_{0:T}, w_x, w_y)} & \bigg[\log \frac{q(z_T \vert z_0)}{p(z_T)} +\sum_{t=2}^T \log \frac{q(z_{t-1} \vert z_0, z_t)}{p_\theta (z_{t-1} \vert z_t, w_x)} \\ & - \log p_\theta (z_0 \vert z_1, w_x) + \log q_\phi (z_0 \vert w_y) - \log \tilde{p} (w_y \vert z_0) \bigg] \end{aligned}\]

$\phi$는 embedding function의 파라미터이며 전체 모델 파라미터 $\theta$의 일부이다. $\tilde{p} (w_y \vert z_0)$는 rounding loss라 부르며 각 위치에 가장 유망한 단어 토큰을 추정한다. 그런 다음 $p_\theta$의 분포에 따라 목적함수는 다음과 같이 간단하게 만들 수 있다.

\[\begin{aligned} \mathcal{L}_{simple} = \mathbb{E}_{q_\phi (z_0, w_x, w_y)} & \bigg[ \sum_{t=2}^T \mathbb{E}_{q(z_t \vert z_0)} \|z_\theta^0 (z_t, w_x, t) - z_0 \|^2 + \|\tilde{\mu} (z_T, z_0)\|^2 \\ &+ \|z_\theta^0 (z_1, w_x, 1) - g_\phi (w_y) \|^2 - \log \tilde{p} (w_y \vert z_0) \bigg] \end{aligned}\]

학습 중에 샘플링 분포 $q_\phi$는 토큰 임베딩의 학습 가능한 파라미터를 포함한다. DiffusionLM의 reparameterization trick을 사용하여 이 파라미터에 역전파가 흐르게 할 수 있다.

Model $z_\theta^0$

$z_\theta^0$를 모델링하기 위해 인코더-디코더 트랜스포머 아키텍처를 사용한다. 입력 시퀀스는 인코더에 의해 모델링되고 출력 시퀀스는 디코더에 의해 모델링된다. 이러한 설계는 DiffuSeq에서 $z_\theta^0$를 모델링하기 위한 인코더만 사용하는 선택과 다르다. 인코더-디코더 아키텍처를 사용하면 입력 시퀀스가 전체 reverse process 동안 인코더를 통해 하나의 forward 계산만 필요하기 때문에 inference (즉, reverse process) 중에 계산상의 편의성이 있다. Reverse process가 출력 시퀀스를 생성하는 데 수천 개의 timestep이 필요하다는 점을 고려하면 계산 리소스를 크게 절약할 수 있다.

Diffusion model은 시퀀스 레벨에서 샘플을 diffuse하고 denoise하므로 denoising process의 각 timestep에 대해 denoising function이 non-autoregreesive한 방식으로 시퀀스 예측을 생성한다. 이와 관련하여 저자들은 causal attention matrix 대신 full attention matrix가 있는 디코더를 사용한다.

2. Self-Conditioning

Reverse process의 각 timestep $t-1$에서 denoising function $z_\theta^0 (z_t, w_x, t)$는 이전에 업데이트된 noisy한 $z_t$만을 기반으로 샘플을 생성하며, function의 예측 \(\hat{z}_0^t = z_\theta^0 (z_{t+1}, w_x, t+1)\)로 직접 컨디셔닝되지 않는다. 각 reverse process는 직전 step에서의 예측 정보를 제거한다.

Analog-Bits 논문은 이전에 예측된 샘플 \(\hat{z}_0^t\)가 보조 입력인 denoising function \(z_\theta^0 (z_t, \hat{z}_0^t, w_x, t)\)을 사용하는 self-conditioning 테크닉을 제안하였다. Self-conditioning은 denoising function이 처음부터 새로운 추정을 만드는 대신 이전 추정을 정제하도록 한다. Analog-Bits와 CDCD는 self-condition이 diffusion model의 성능을 향상시킬 수 있다는 것을 경험적으로 증명하였다.

저자들은 self-conditioning을 본 논문의 모델에 통합하였다. 50%의 확률로 \(z_\theta^0 (z_t, \hat{z}_0^t, w_x, t)\)는 \(\hat{z}_0^t = 0\)으로 세팅하여 학습되고, 나머지 50%의 확률로 먼저 \(\hat{z}_0^t\)를 \(z_\theta^0 (z_t, 0, w_x, t)\)으로 추정한 다음 이를 self-conditioning 학습에 사용한다. 두번째의 경우에는 먼저 추정된 \(\hat{z}_0^t\)에 역전파가 흐르지 않게 한다. 추가 학습 시간은 25%보다 적다고 한다.

3. Adaptive Noise Schedule

비전 및 텍스트 diffusion model 분야에서 서로 다른 noise schedule이 샘플 품질과 likelihood 추정 측면에서 diffusion model의 성능에 잠재적으로 긍정적인 영향을 미칠 수 있음이 입증되었다. 서로 다른 noise schedule은 step마다 실제 샘플에 추가되는 서로 다른 레벨의 noise를 제어하므로 step마다 denoising의 어려움이 달라진다. 저자들은 \(\hat{z}_0\) 예측의 어려움이 timestep에 따라 선형적으로 증가해야 한다는 휴리스틱을 제안한다. 이 휴리스틱에서 각 denoising timestep에 대해 복구된 noise 레벨은 timestep에 걸쳐 고르게 분포되어야 한다. 저자들은 각 step $t$에 대한 학습 loss

\[\begin{equation} \mathbb{E}_{q_\phi (w_x, w_y, z_t)} \| z_\theta^0 (z_t, \hat{z}_0^t, w_x, t) - z_0 \|^2 \end{equation}\]

로 denoising의 어려움을 측정한다.

출력 시퀀스의 서로 다른 토큰이 서로 다른 양의 정보를 전달할 수 있고 생성의 난이도가 다를 수 있다는 점을 고려하면 각 토큰은 서로 다른 noise schedule에 해당해야 한다. 저자들은 다른 위치의 토큰에 대해 다른 noise schedule을 설정한다.

Timestep $t$와 토큰 위치 $i$에 대한 학습 loss를 $\mathcal{L}_t^i$로 나타낸다. Noise schedule을 나타내는 $\bar{\alpha}_t^i$의 schedule을 사용한다. Noise schedule의 디자인 (ex. DiffusionLM의 sqrt)에서 초기화하여 loss $\mathcal{L}_t^i$를 추적하고 linear interpolation을 사용하여 각 $i$에 대해 $\mathcal{L}_t^i$와 $\bar{\alpha}_t^i$ 사이의 매핑 $\mathcal{L}_t^i = M_i (\bar{\alpha}_t^i)$를 피팅한다. 이상적으로 학습 loss는 $\bar{\alpha}_t^i$에 대해 단조로워야 한다. 그러나 경험적 loss 추정치의 오차로 인해 학습 loss가 국부적으로 단조롭지 않을 수 있다. 이 문제를 완화하고 더 부드러운 매핑에 맞추기 위해 $\mathcal{L}_s^i$와 $\bar{\alpha}_s^i$의 coarse-grained discretization을 형성한다.

\[\begin{equation} \mathcal{L}_s^i = \frac{1}{M} \sum_{t=s \times M}^{s \times (M+1)} \mathcal{L}_t^i \\ \bar{\alpha}_s^i = \frac{1}{M} \sum_{t=s \times M}^{s \times (M+1)} \bar{\alpha}_t^i \\ s = \bigg\lfloor \frac{t}{M} \bigg\rfloor \end{equation}\]

여기서 $M$은 $t$를 downsampling하는 stride이고 $\lfloor \cdot \rfloor$는 내림 연산자이다.

$\mathcal{L}_s^i = M_i (\bar{\alpha}_s^i)$를 사용하면 inverse mapping $\bar{\alpha}_t^i = M_i^{-1} (\mathcal{L}_t^i)$를 유도할 수 있다. 그러면 $\mathcal{L}_t^i$에서 값을 고르게 취하여 noise schedule $\bar{\alpha}_t^i$를 샘플링할 수 있다. 따라서 서로 다른 timestep에 걸쳐 학습 loss를 고르게 분산시키는 최종 adaptive noise schedule $\bar{\alpha}_t^i$를 얻을 수 있다. 학습이 진행됨에 따라 학습 업데이트당 한 번씩 위에서 언급한 절차를 반복하여 학습된 noise schedule을 보정한다.

각 토큰 위치에서 padding token에 대한 학습 loss를 제외합니다. 더 큰 위치 인덱스에 있는 토큰의 경우 이러한 위치에 있는 대부분의 토큰은 다른 샘플에 대한 padding token이다. Padding token의 loss는 위치에 대한 noise schedule을 잘못 이끌 수 있다. 이는 padding token 생성이 단어 토큰 생성보다 훨씬 쉽기 때문이며 padding token은 더 긴 시퀀스의 생성 성능을 방해할 수 있다.

Experiments

• 데이터셋
  • Commonsense Conversation Dataset (CCD): open domain dialogue
  • Quasar-T: question generation
  • Wiki-Auto: text simplification
  • Quora Question Pairs (QQP): paraphrase
  • IWSLT14: machine translation
• Implementation Details
  • 12개의 layer를 가진 인코더-디코더 Transformers를 사용 (GeLU activation)
  • 최대 입력 시퀀스는 128, 최대 출력 시퀀스는 64, 단어 임베딩 차원은 128
  • Diffusion step 2000, 초기 noise schedule은 DiffusionLM의 sqrt
  • 번역 task의 경우 Byte Pair Encoding (BPE)로 vocabulary 구축 (vocabulary 크기는 10,000), 다른 task는 BERT-BASE-UNCASED의 vocabulary 사용.
  • Batch size 1024, 100만 step 학습, learning rate $10^{-4}$ (warm-up 10,000 step, linearly-decreasing schedule)
  • 학습 중에 noise schedule은 20,000 step마다 업데이트됨
  • Inference 중에는 maximum Bayes risk (MBR)를 적용하여 디코딩

1. Main Results

다음은 SeqDiffuSeq를 baseline과 다양한 task에 대하여 비교한 표이다.

다음은 기계번역에 대한 결과이다.

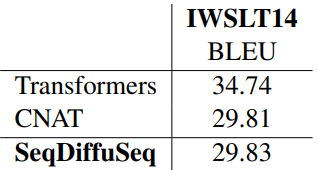
AR baseline과 비교하여 번역 성능의 불일치가 있지만 SeqDiffuSeq은 강력한 NAR baseline으로 경쟁력 있는 결과를 얻을 수 있다.

2. Ablation Study

다음은 IWSLT14 DE-EN validation set에 대한 ablation study 결과이다.

결과는 adaptive noise schedule과 self-conditioning의 효과를 보여준다. 서로 다른 n-gram의 BLEU score에서 trigram과 quadrigram의 점수가 더 많이 변동하는 것으로 나타났다. 이것은 두 테크닉 모두 더 긴 시퀀스를 개선하여 생성된 텍스트의 품질을 향상시킨다는 것을 보여준다.

3. Analysis

Time Schedule

다음은 adaptive noise schedule을 시각화한 그래프이다. origin은 sqrt schedule이며 token_$i$는 위치 $i$의 토큰에 대한 noise schedule이다.

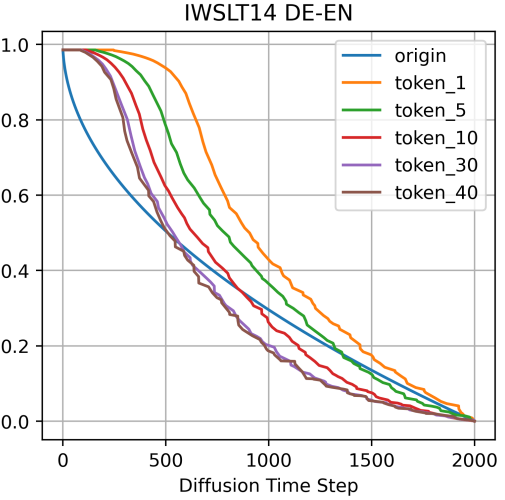
그래프는 adaptive noise schedule이 초기 라인에서 많이 벗어나고 토큰 위치에 따라 noise schedule이 다르다는 것을 보여준다.

Diffusion timestep의 시작 부분에서 $\bar{\alpha}_t^i$의 변화는 서로 다른 토큰 위치에 걸쳐 다소 부드럽다. 학습 loss가 timestep에 대해 선형적으로 증가한다는 점을 고려하면 적은 양의 noise가 diffusion process 초기에 상대적으로 큰 loss 변화를 일으킬 것임을 나타낸다.

위치 순서가 더 큰 토큰의 경우 noise schedule 라인이 왼쪽 아래 방향으로 이동한다. 이것은 위치 순서가 더 큰 토큰이 추가된 noise에 더 강하다는 것을 나타낸다.

Inference Speed

Diffusion model의 주요 관심사 중 하나는 inference 속도이다. Inference 시간 측면에서 SeqDiffuSeq와 DiffuSeq를 비교한다. 저자들은 QQP에 대한 실험을 수행하고 두 모델 모두에 대해 inference batch size를 50으로, diffusion timestep을 2000으로 설정다.

위 표에 표시된 결과는 단일 NVIDIA V100 GPU에서 DiffuSeq와 비교하여 SeqDiffuSeq가 3.56배 빠르게 하나의 텍스트 샘플 배치를 생성함을 보여준다. 가속은 주로 다음에서 발생한다.

1. SeqDiffuSeq는 인코더의 forward 계산을 한 번만 필요로 하는 반면, DiffuSeq는 각 step의 입력 시퀀스에서 forward 계산을 실행해야 한다.
2. SeqDiffuSeq의 디코더는 출력 시퀀스만 모델링하면 되는 반면 DiffuSeq는 입력 및 출력 시퀀스 모두의 연결을 모델링해야 한다. 따라서 각 step에 대해 SeqDiffuSeq의 시퀀스 길이는 DiffuSeq의 절반에 불과하다.

Case Study

저자들은 QQP에서 3가지 케이스를 선택하고 SeqDiffuSeq의 생성 프로세스를 조사하였다. 케이스들에서 SeqDiffuSeq가 합리적인 텍스트 시퀀스를 생성할 수 있음을 보여준다. 생성 프로세스는 다음을 보여준다.

1. SeqDiffuSeq는 샘플링 초기 단계에서 토큰을 생성하여 출력 시퀀스 길이를 결정한다.
2. 생성 프로세스는 왼쪽에서 오른쪽으로의 정제 순서를 따르는 것 같다.
3. 빨간색으로 표시된 것처럼 생성된 시퀀스에 토큰 반복이 존재하더라도 샘플링 중에 토큰의 위치는 변경되지 않는다.