arXiv 2022. [Paper]
Robin Scheibler, Youna Ji, Soo-Whan Chung, Jaeuk Byun, Soyeon Choe, Min-Seok Choi
LINE Corporation | Naver Corporation
31 Oct 2022

Introduction

Source separation(SS)은 혼합된 신호에서 원하는 신호를 복구하는 데 사용할 수 있는 기술을 말한다. 광범위한 어플리케이션이 있지만 본 논문은 단일 채널 오디오와 음성에 중점을 둔다. 이것은 여러 신호가 단일 혼합된 신호에서 복구되는 underdetermined problem이다. 이 분야의 초기 성공은 Non-negative Matrix Factorization (NMF)와 같은 방법으로 이루어졌다. 데이터 기반 방법과 DNN(심층 신경망)을 통해 놀라운 발전이 이루어졌다.

먼저 입력 스펙트로그램의 시간-주파수 bin이 source별로 cluster되는 embedding space를 생성하도록 DNN이 학습되는 deep clustering에 대해 살펴본다. 그런 다음 bin cluster에 해당하는 마스크를 생성하고 스펙트로그램을 곱하여 격리된 source를 복구할 수 있다. 그런 다음 이러한 방법은 마스크 값을 직접 예측하는 네트워크로 발전했다. 이러한 모든 데이터 기반 방법은 근본적인 source 순열의 모호성을 해결해야 한다. 즉, source에 대해 고유한 선호 순서가 없다. 이것은 일반적으로 permutation invariant training(PIT)에 의해 처리된다. PIT에서는 source의 모든 순열에 대해 목적 함수를 계산하고 기울기를 계산하기 위해 최소값을 갖는 것을 선택한다. 최근에 Conv-TasNet 또는 dual-path transformer와 같은 매우 강력한 시간 도메인 baseline이 제안되었다.

저자들은 또한 시간-주파수 도메인에서 all-attention 기반 multi-scale 네트워크 WaveSplit과 최근의 state-of-the-art TF-GridNet을 언급한다. 이러한 최근의 모든 접근법은 scale-invariant signal-to-distortion ratio (SI-SDR)와 같은 discriminative한 목적 함수로 학습된다. NMF와 같은 전통적인 방법을 제외하고 생성 모델을 활용하는 접근 방식은 거의 없다. 한 가지 예외는 speaker별 생성 모델을 적대적으로 학습시키고 이를 separation에 사용한다.

Discriminative한 방법과 달리 생성 모델링을 사용하면 복잡한 데이터 분포를 근사화할 수 있다. 최근 diffusion 기반 모델링으로도 알려진 score 기반 생성 모델링 (SGM)은 특히 이미지 생성 영역에서 빠르고 인상적인 발전을 이루었다. SGM은 대상 분포의 샘플을 Gaussian noise로 점진적으로 변환하는 forward process를 정의한다. Score 함수, 즉 로그 확률의 기울기가 주어지면 noise에서 시작하여 reverse process를 실행하여 목표 분포를 샘플링할 수 있다. 결정적으로 score 함수는 보통 모르지만 간단한 학습 전략을 사용하여 DNN으로 근사화할 수 있다.

최근 접근 방식은 score-matching과 Langevin sampling의 조합의 결과입니다. 다양한 접근 방식을 통합하기 위해 두 가지 프레임워크가 제안되었다. 하나는 그래픽 모델을 기반으로 하고 다른 하나는 확률적 미분 방정식(SDE)을 기반으로 한다. SGM은 음성 합성, 음성 복원, 대역폭 확장에 성공적으로 적용되었다. 그러나 diffusion 기반 음성 분리 방법은 아직 제안되지 않았다.

본 논문은 음성 신호 분리를 위한 최초의 diffusion 기반 접근법을 제안함으로써 이러한 격차를 메운다. 제안된 DiffSep은 분리된 신호에서 시작하여 평균적으로 혼합된 신호로 수렴하는 신중하게 설계된 SDE를 기반으로 한다. 그런 다음 해당 reverse-time SDE를 해결하여 혼합된 source에서 개별 source를 복구할 수 있다. 저자들은 inference 프로세스 초기에 source 할당의 모호성을 해결하는 score-matching 네트워크에 대한 수정된 학습 전략을 제안한다.

Background

1. Notation and Signal Model

$N$개의 실수 값 샘플 $s_k \in \mathbb{R}^N$로 오디오 신호를 나타낸다. $K$ 개의 source를 사용한 간단한 혼합 모델을 도입한다.

\[\begin{equation} y = \sum_{k=1}^K s_k \end{equation}\]

이 모델은 추가 source를 추가하여 환경 소음, 잔향 및 기타 degradation을 설명할 수 있다. 모든 source 신호를 concat하여 $\mathbb{R}^{KN}$에서 벡터를 얻는다. 이 표기법에서 분리된 source의 벡터와 벡터의 평균값을 다음과 같이 정의합니다.

\[\begin{equation} s = [s_1^\top, \cdots, s_K^\top]^\top, \bar{s} = K^{-1} [y^\top, \cdots, y^\top]^\top \end{equation}\]

시불변 혼합 연산을 $(A \otimes I_N)$와 같이 곱셈으로 정의할 수 있다. 여기서 $I_N$은 $N \times N$ 항등 행렬이고 $A$는 $K \times K$ 행렬이며 $\otimes$는 Kronecker product이다. 벡터 $v \in \mathbb{R}^{KN}$를 이러한 행렬과 곱하는 것은 길이 $K$의 모든 하위 벡터에 대해 $v$에서 간격 $N$으로 요소를 취하여 곱하는 것과 같다.

\[\begin{equation} ((A \otimes I_N) v)_{kN+n} = \sum_{l=1}^K A_{kl} v_{lN+n} \\ k = 1, \cdots, K, \quad n = 1, \cdots, N \end{equation}\]

표기를 간단하게 하기 위해 일반적인 행렬 곱으로 표현한다.

\[\begin{equation} Av := (A \otimes I_N) v \end{equation}\]

다음으로 projection 행렬을 정의한다.

\[\begin{equation} P = K^{-1} \mathbb{1} \mathbb{1}^\top, \quad \bar{P} = I_K - P \end{equation}\]

$\mathbb{1}$은 all one vector이다. 행렬 $P$는 평균값의 subspace에 project하고 $\bar{P}$는 orthogonal complement이다.

\[\begin{equation} Ps = \bar{s} \end{equation}\]

2. SDE for Score-based Generative Modelling

Diffusion process는 다음과 같은 SDE로 나타낼 수 있다.

\[\begin{equation} dx_t = f(x_t, t) dt + g(t)dw_t \end{equation}\]

이에 대응되는 reverse-time SDE는 다음과 같다.

\[\begin{equation} dx_t = -[f(x_t, t) - g(t)^2 \nabla_{x_t} \log p_t (x_t)] dt + g(t) d \bar{w} \end{equation}\]

Reverse-time SDE는 바로 풀 수 없다. SGM의 주요 아이디어는 신경망 $q_\theta (x, t) \approx \nabla_x \log p_t (x)$를 학습시키는 것이다. 근사가 충분히 잘 되었다면 $\nabla_{x_t} \log p_t (x_t)$를 $q_\theta (x, t)$로 바꾼 후 reverse-time SDE는 수치적으로 풀 수 있다.

SGM은 처음에 매우 높은 품질의 합성 이미지 생성에 대하여 광범위하게 채택하였다. 따라서 SGM은 음성 합성을 위한 논리적인 후보이다. 이 영역에서 타겟 음성에 적응적으로 noise를 형성하는 몇 가지 접근 방식이 제안되었다. 하나는 로컬 신호 에너지를 사용하는 반면 다른 하나는 타겟 스펙트로그램에 따라 noise의 상관 관계를 도입한다.

대역폭 확장 및 복원도 오디오의 누락된 부분을 생성해야 하며 고품질 diffusion 기반 접근 방식이 제안되었다. Diffuse와 CDiffuse는 noisy한 음성 신호를 향상시키기 위해 조건부 diffusion을 사용한다. 또한 음성 향상을 위해 SGMSE는 다음과 같은 forward model에 해당하는 reverse-time SDE 해결을 기반으로 하는 또 다른 접근 방식을 제안했다.

\[\begin{equation} dx_t = \gamma (y - x_t) dt + g(t) dw, \quad x_0 = s \end{equation}\]

이것이 Ornstein-Uhlenbeck SDE로, forward 방향으로 깨끗한 음성 $s$를 noisy한 음성 $y$ 쪽으로 점진적으로 만든다.

Diffusion-based Source Separation

본 논문은 source separation 문제에 SGM을 적용하기 위한 프레임워크를 제안한다. 본질적으로 시간이 지남에 따라 source 간 diffusion과 혼합이 모두 발생하는 forward SDE를 설계한다. 프로세스의 각 step은 극소량의 noise를 추가하고 극소량의 혼합을 수행하는 것으로 설명할 수 있다. 이는 다음 SDE로 공식화될 수 있다.

\[\begin{equation} dx_t = - \gamma \bar{P}x_t dt + g(t) dw, \quad x_0 = s \end{equation}\]

Variance Exploding SDE의 diffusion coefficient

\[\begin{equation} g(t) = \sigma_\textrm{min} \bigg( \frac{\sigma_\textrm{max}}{\sigma_\textrm{min}} \bigg)^t \sqrt{2 \log \bigg( \frac{\sigma_\textrm{max}}{\sigma_\textrm{min}} \bigg)} \end{equation}\]

를 사용한다. SDE는 $t$가 커짐에 따라 평균 $\mu_t$가 $t = 0$에서의 분리된 신호의 벡터에서 혼합 벡터 $\bar{s}$로 이동한다는 흥미로운 속성을 가지고 있다. 이것은 다음 Theorem 1로 공식화된다.

$x_t$의 주변 분포가 평균과 공분산 행렬이

\[\begin{equation} \mu_t = (1 - e^{-\gamma t}) \bar{s} + e^{-\gamma t}s \\ \Sigma_t = \lambda_1 (t) P + \lambda_2 (t) \bar{P} \end{equation}\]

인 가우시안 분포이고 $\xi_1 = 0, \xi_2 = \gamma, \rho = \sigma_\textrm{max} / \sigma_\textrm{min}$이면,

\[\begin{equation} \lambda_k (t) = \frac{\sigma_\textrm{min}^2 (\rho^{2t} - e^{-2 \xi_k t}) \log \rho}{\xi_k + \log \rho} \end{equation}\]

이다.


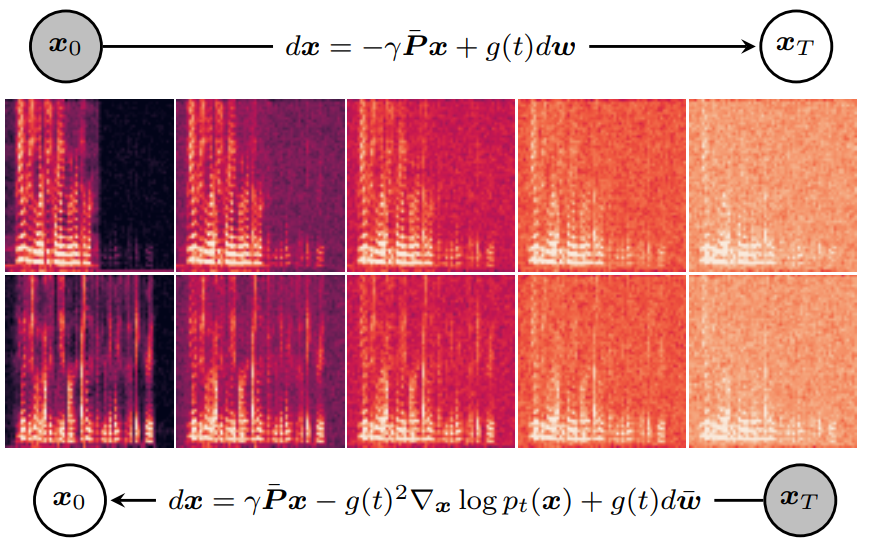
위 그림은 실제 혼합된 신호에 대한 예시를 보여준다. 샘플 $x_t$에 대한 명시적 표현은 아래와 같다.

\[\begin{equation} x_t = \mu_t + L_t z, \quad z \sim \mathcal{N} (0, I_{KN}) L_t = \lambda_1 (t)^{1/2} P + \lambda_2 (t)^{1/2} \bar{P} \end{equation}\]


위 그림은 시간에 따른 $x_t$의 몇몇 파라미터들의 변화를 보여준다. $\gamma$를 조정하면 $\mu_T$와 $\bar{s}$의 차이를 임의로 작게 만들 수 있다. 또한, 혼합 프로세스로 인해 두 source에 추가된 noise의 상관 관계가 시간이 지남에 따라 증가함을 관찰하였다.

음성 향상에 대한 이전 연구는 비선형 변환을 사용하여 short-time Fourier transform (STFT) 도메인에서 diffusion process를 성공적으로 적용했다. 본 논문이 제안하는 접근 방식은 시간 도메인 또는 STFT와 같은 선형 변환 도메인에서 동일하게 적용될 수 있다. 그러나 SDE의 프로세스는 source의 선형 혼합을 모델링하기 때문에 비선형 변환을 적용할 수 없다. 대신 시간 도메인에서 diffusion process를 수행하지만 비선형 STFT 도메인에서 네트워크를 사용한다.

1. Inference

Inference 중에는 score-matching network $q_\theta (x, t, y) \approx \nabla_x \log p_t (x)$을 사용하여 reverse-time SDE를 풀어 separation을 한다. 프로세스의 초기값은

\[\begin{equation} \bar{x}_T \sim \mathcal{N} (\bar{s}, \Sigma_T I_{KN}) \end{equation}\]

에서 샘플링된다. 그런 다음 predictor-corrector 방법을 적용하여 reverse-times SDE를 푼다. Prediction step은 reverse diffuse sampling에 의해 수행된다. Correction step은 annealed Langevin sampling에 의해 수행된다.

2. Permutation and Mismatch-aware Training Procedure

본 논문은 score network $q_\theta (x, t, y)$를 학습시키기 위해 살짝 수정된 score-matching 과정을 제안한다. 하지만 먼저 일반적인 과정을 따른다. Theorem 1에 의해 score function은 closed-form 표현을 가진다. SGMSE과 비슷한 계산으로

\[\begin{equation} \nabla_{x_t} \log p (x_t) = -\Sigma_t^{-1} (x_t - \mu_t) = - L_t^{-1} z \end{equation}\]

를 얻는다. 학습 loss는 다음과 같다.

\[\begin{aligned} \mathcal{L} &= \mathbb{E}_{x_0, z, t} \| q_\theta (x_t, t, y) + L_t^{-1} z \|_{\Sigma_t}^2 \\ &= \mathbb{E}_{x_0, z, t} \| L_t q_\theta (x_t, t, y) + z \|^2 \end{aligned}\]

$z \sim \mathcal{N}(0, I_{KN}), t \sim \mathcal{U} (t_\epsilon, T)$이고 $x_0$를 데이터셋에서 랜덤하게 선택한다. $\Sigma_t$로 유도된 norm을 사용하며, 이는 NCSN에서 제안된 가중치 방법과 동등하다. 이 방법은 비용의 크기를 $\Sigma_t$와 독립적으로 만들고 $L_t$의 역행렬 계산을 피할 수 있다.

그러나 저자들은 방금 설명한 과정으로만 학습할 때 inference 시간에 성능이 좋지 않음을 발견했으며, 두 가지 문제를 확인했다. 첫째, 의 $\mathbb{E}[\bar{x}_T] = \bar{s}$와 $\mu_T$ 사이에 불일치가 있다. $\mu_T$는 약간 다른 비율의 source를 포함하지만 $\bar{s}$는 그렇지 않다. 둘째, 네트워크는 source를 출력할 순서를 결정해야 한다. 이것은 일반적으로 PIT 목적 함수로 해결된다. 이러한 문제를 해결하기 위해 저자들은 모델 불일치를 포함하는 방식으로 네트워크를 학습할 것을 제안한다.

각 샘플에 대하여 $1 - p_T, p_T \in [0,1]$의 확률로 일반 score-matching 과정을 적용한다. $p_T$의 확률로 $t = T$로 설정하고 다음과 같은 대체 loss를 최소화한다.

\[\begin{equation} \mathcal{L}_T = \mathbb{E}_{x_0, z} \min_{\pi \in \mathcal{P}} \| L_T q_\theta (\bar{x}_T, T, y) + z + L_T^{-1} (\bar{s} - \mu_T (\pi)) \|^2 \end{equation}\]

$\mathcal{P}$는 source 순열의 집합이며, $\mu_T (\pi)$는 순열 $\pi$로 계산한 $\mu_T$이다. 이 목적 함수의 합리성은 score network가 noise와 모델 불일치를 모두 제거하는 방법을 학습한다는 것이다. 음성 향상의 경우 source 순서에 모호성이 없으며 순열에 대한 최소화를 제거할 수 있다.

Experiments

  • 데이터셋: WSJ0_2mix dataset (음성 분리), VoiceBank-DEMAND dataset (음성 향상)
  • 모델: Noise conditioned score-matching network (NCSN++)
    • STFT와 STFT의 inverse layer (iSTFT)가 network를 감싸고 추가로 STFT 이후에 비선형 변환 $c(x)$와 iSTFT 이전에 c(x)의 inverse를 적용한다.
\[\begin{equation} c(x) = \beta^{-1} |x|^\alpha e^{j \angle x} \\ c^{-1} (x) = \beta |x|^{1 / \alpha} e^{j \angle x} \end{equation}\]
  • Hyperparameter
    • $\gamma = 2$, $\sigma_\textrm{min} = 0.05$, $\sigma_\textrm{max} = 0.5$, $\alpha = 0.5$, $\beta = 0.15$
    • 음성 분리: $p_T = 0.1$, batch size 48, learning rate 0.0005, 1000 epochs
    • 음성 향상: $p_T = 0.3$, PriorGrad로 noise 생성, batch size 16, learning rate 0.0001, 160 epochs

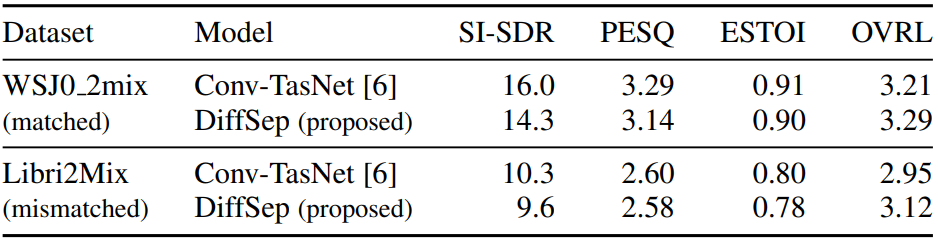
Separation

다음은 WSJ0_2mix와 Libri2Mix (clean) dataset에 대한 음성 분리 결과를 나타낸 표이다.


다음은 깨끗한 source들(아래)과 이들의 혼합에 제안된 방법을 적용하여 얻은 분리된 음성(위)의 스펙트로그램이다.


왼쪽에서 오른쪽으로 3개의 샘플은 SI-SDR로 분류된 하위 10%, 중간 80%, 상위 10% 샘플에서 무작위로 선택되었다. 샘플의 SI-SDR은 상단에 표시됩니다. 낮은 품질의 샘플에서는 스펙트로그램이 좋아 보이지만 발생하는 source의 순열 발생을 막는 것을 볼 수 있다.

Enhancement

다음은 VoiceBank-DEMAND dataset에 대한 음성 향상 결과를 나타낸 표이다.