Blogs

arXiv 2023. [Paper]
Jaemoo Choi, Yesom Park, Myungjoo Kang
Seoul National University
20 Feb 2023

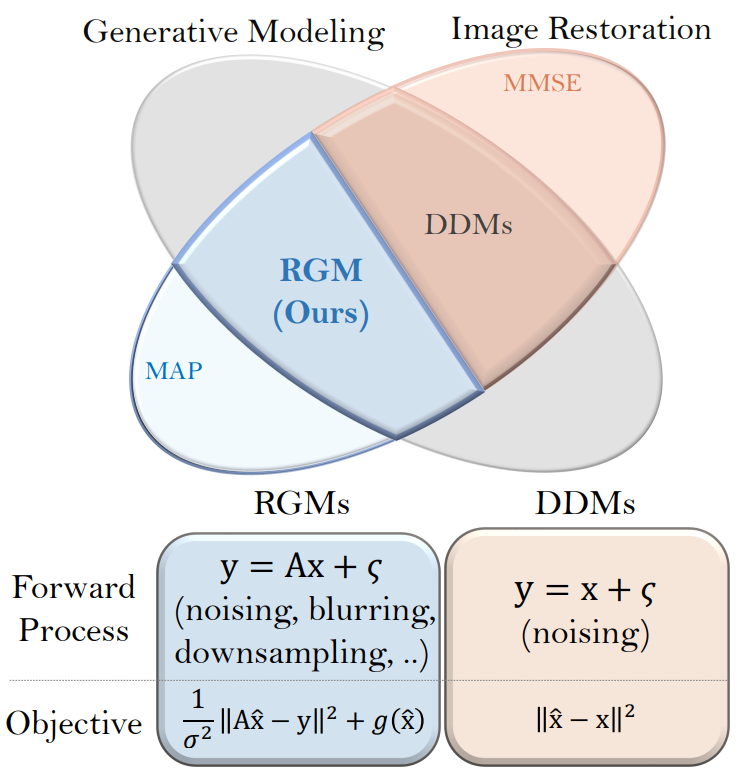
Introduction

생성 모델링은 모델이 데이셋이 분포된 방식을 설명하고 분포에서 새 샘플을 생성하는 방법을 배우는 machine learning task이다. 가장 널리 사용되는 생성 모델은 주로 데이터 분포를 tractable한 latent 분포로 연결하는 선택이 다르다. 최근 몇 년 동안 denoising diffusion model (DDM)이 놀라운 결과를 보여 상당한 관심을 끌었다. DDM은 데이터를 점진적으로 Gaussian noise로 변환하는 forward diffusion process에 의존하며 noising process를 reverse시키는 방법을 학습한다. 엄청난 성공에도 불구하고 점진적인 denoising process로 인해 낮은 inference 효율성이 발생한다. Latent 변수를 데이터 분포로 되돌리려면 denoising process에서 수백 또는 수천 번의 네트워크 평가가 필요한 경우가 많다. 많은 후속 연구에서 inference 속도 향상 또는 다른 생성 모델과의 접목을 고려하였다.

본 논문에서는 다른 관점에 주목한다. 손상된 이미지에서 원본 이미지를 복구하기 위한 inverse problem 계열인 image restoration (IR) 관점에서 DDM을 해석한다. 손상은 noising과 downsampling을 비롯한 다양한 형태로 발생한다. IR 관점에서 DDM은 denoising task에만 초점을 맞춘 최소 평균 제곱 오차(MMSE) 추정을 기반으로 하는 IR 모델로 간주할 수 있다. 수학적으로 IR은 고유한 해를 허용하지 않아 재구성의 불안정성을 초래한다는 점에서 ill-posed inverse problem이다. 이로 인해 MMSE는 무례한 결과를 생성한다. DDM은 비용이 많이 드는 확률적 샘플링을 활용하여 이 문제를 완화하며, 확률적 샘플링은 DDM 관련 논문에서 없어서는 안 될 도구로 여겨져 왔다.

저자들은 여기에서 영감을 받아 restoration-based generative model (RGM)이라 부르는 새로운 유연한 생성 모델 계열을 제안한다. 본 논문은 대체 목적 함수로 IR에서 주로 사용되는 maximum a posteriori (MAP) 기반 정규화를 채택하며, 이 접근 방식은 비용이 많이 드는 반복 샘플링을 수행하는 대신 사전 지식으로 data fidelity loss를 정규화하여 ill-posedness를 우회한다. 사전 지식은 다양한 방식으로 활용될 수 있다. 또한 열화 과정을 자유롭게 설계할 수 있다. 이 두 변수가 있는 RGM에는 몇 가지 이점이 있다.

Implicit Prior knowledge

손으로 만든 많은 정규화 체계는 해가 부드러움이나 희소성과 같은 특정 속성을 충족하도록 권장한다. 그러나 밀도 추정을 위해 KL divergence 또는 Wasserstein distance와 같은 통계적 거리를 학습하기 위해 prior term을 parameterize한다. 또한 ill-posedness를 더욱 완화하기 위해 랜덤 보조 변수를 도입한다. MAP 기반 추정은 DDM의 밀도 추정 기능을 유지하면서 계산 비용이 훨씬 더 적다.

Various Forward process

DDM은 Gaussian noising process에 묻혀 있다. 반면 RGM의 forward process의 유동성은 데이터 분포가 단순 분포로 변환되는 방식에 따라 생성 모델의 동작이 크게 영향을 받기 때문에 모델 성능을 향상시킨다. 이미지를 block averaging하여 차원을 점진적으로 줄이는 degradation process를 설계하여 성능을 향상시킨다.

Method

1. MAP-based Estimation for Generation

DDM은 denoising에 특화된 MMSE-grounded IR 모델로 간주할 수 있다. 이 관찰은 유연한 생성 모델 계열의 설계에 대한 새로운 관점을 제공한다. MMSE의 대안으로 다음 식에 기반한 새로운 생성 모델을 제안한다.

\[\begin{equation} \mathbb{E}_{x \sim p_\textrm{data}, y \sim \mathcal{N}(x, \sigma^2 I)} \bigg[ \frac{1}{2 \sigma^2} \| G_\theta (y) - y \|_2^2 + \lambda g (G_\theta (y)) \bigg] \end{equation}\]

첫번째 항은 데이터 fidelity를 측정하고 두번째 항은 데이터 분포의 사전 지식을 전달한다.

이것은 고차원 이미징 문제에 대한 표준 접근 방식으로 채택되었으며 많은 응용 프로그램에서 MMSE보다 더 관련성이 높은 것으로 알려져 있다. MAP 기반 접근 방식은 해에 대한 사전 정보를 활용함으로써 비용이 많이 드는 샘플링을 사용하지 않고 inverse problem의 ill-posedness를 완화한다. 따라서 관련있는 prior term을 신중하게 만드는 것이 중요하다.

Alleviation of ill-posedness

일반 denoising task와 달리 데이터 분포를 학습하려면 이미지를 Gaussian noise에 연결해야 한다. Noise level이 증가함에 따라 하나의 왜곡된 관측에는 여러 해가 존재하며 이는 ill-posedness가 깊어짐을 의미한다. 따라서 generator $G_\theta$는 데이터 분포를 보다 풍부하게 표현하기 위해 degrade된 이미지에서 다양한 복원을 복구할 수 있어야 한다. Regularization term 자체로는 이러한 모든 문제를 해결하기 어렵기 때문에 랜덤 보조 변수 $z \sim \mathcal{N} (z \vert 0,I)$을 도입하여 ill-posedness를 완화한다. 즉, random variable $z$를 $G_\theta$의 입력으로 사용한다. $G_\theta (y, z)$는 서로 다른 $z$에 대해 다양한 복원을 생성하므로 데이터 분포를 충실하게 복구하기가 더 쉽다.

Implicit Prior Knowledge

밀도 추정을 위해 데이터 분포에 대한 지식은 prior term $g$에 적절하게 인코딩되어야 한다. 그러나 데이터의 명시적 밀도를 알 수 없기 때문에 prior를 학습하기 위해 $g$를 parameterize한다. 각 forward step에 대해 $z$와 함께 생성기 $G_\theta$에 대한 새로운 목적 함수는 다음과 같다.

\[\begin{equation} \mathbb{E}_{x \sim p_\textrm{data}, y \sim \mathcal{N} (x, \sigma^2 I), z \sim \mathcal{N}(0, I)} \bigg[ \frac{1}{2 \sigma^2} \| G_\theta (y, z) - y \|_2^2 + \lambda g_\phi (G_\theta (y, z)) \bigg] \end{equation}\]

$g_\phi$는 $\phi$로 parameterize된 학습 가능한 prior term이다. 예를 들어, $G_\theta$와 함께 학습된 discriminator $D_\phi$를 사용하여 prior term을

\[\begin{equation} g_\phi (x) = \log (1 - D_\phi (x)) - \log D_\phi (x) \end{equation}\]

로 parameterize하여 데이터의 암시적 표현을 학습할 수 있다. $D_\phi$가 최적에 가까워지면 $g_\phi$의 기대값은 KL divergence (KLD) $D_{KL} (p_\theta \vert p_\textrm{data})$에 가까워지며, $\lambda = 1$인 경우 목적 함수가 다음과 같아진다.

\[\begin{equation} \mathbb{E}_{x \sim p_\textrm{data}, y \sim \mathcal{N} (x, \sigma^2 I)} \bigg[ D_{KL} (p_\theta (x \vert y) \| p(x \vert y)) \bigg] + \mathcal{H} (p_\theta) \end{equation}\]

$\mathcal{H}$는 엔트로피이고 $p_\theta$는 $G_\theta$가 생성한 분포이다.

Prior term이 미리 정의된 기존 IR 논문과 달리 본 논문의 접근 방식은 $G_\theta$와 조정하여 prior term을 학습하려고 시도한다. 이 end-to-end 학습을 통해 MAP에서 영감을 받은 체계가 더 유망한 성능을 보일 수 있다. 또한, 본 논문의 프레임워크는 위에 예시된 KLD에 대한 discriminative learning에 얽매이지 않고 $g_\phi$의 선택에 있어 넓은 자유도를 갖는다는 점에 주목할 가치가 있다. 결과적으로 maximum mean discrepancy (MMD)와 distributed sliced Wasserstein distance (DSWD)를 장착하여 prior term을 추가로 설계한다.

Small Denoising Steps

DDM의 주요 단점은 샘플링 비효율성이다. Regularization term $g$를 채택함으로써 본 논문의 접근 방식은 시간이 많이 걸리는 샘플링의 짐을 덜 수 있는 방법을 제공하고 상당히 작은 denoising step을 가능하게 한다. 작은 degradation의 경우 한 번에 복원된 이미지를 얻을 수 있다. 그러나 복원이 Gaussian noise에서 시작되므로 데이터 분포가 완전히 추정되지 않는다. 따라서 생성을 반복적으로 수행한다. CIFAR10에 대한 실험에서 4 denoising step으계로 고품질 샘플을 생성한다.

2. Extension to General Restoration

앞서 MAP 목적 함수를 기반으로 하는 denoising 생성 모델을 제안했다. 그러나 IR 관점에서 forward process를 Gaussian noise로 ($A = I$)로 제한할 필요는 없으며 degradation matrix $A$와 noise 계수 $\Sigma$의 모든 계열로 일반화할 수 있다. 일반 forward process를 활용한 일반화된 loss function은 다음과 같다.

\[\begin{equation} \mathbb{E}_{x \sim p_\textrm{data}, y \sim \mathcal{N}(Ax, \Sigma), z \sim \mathcal{N}(0,I)} \bigg[ \lambda g_\phi (G_\theta (y, z)) + \frac{1}{2} \bigg\| (\Sigma^\dagger)^{\frac{1}{2}} (A \cdot G_\theta (y, z) - y) \bigg\|_2^2 \bigg] \end{equation}\]

따라서 RGM은 모든 forward process에 스며들 수 있는 유연한 구조를 가지고 있으며 새로운 생성 모델을 설계하는 데 도움이 된다. 여기서 super-resolution (SR) 기반의 새로운 모델을 제안한다.

Multi-scale RGM

대부분의 DDM은 개별 픽셀에 noise를 추가하여 diffusion process 중에 이미지 크기를 유지한다. 결과적으로 이미지 공간의 submanifold보다 훨씬 더 큰 픽셀 공간의 차원만큼의 latent를 필요로 하기 때문에 매우 비효율적이다. 이것에 동기를 부여하여 A를 2$\times$2 픽셀 값을 평균화하는 block averaging filter로 사용한다. 각 coarsening step에서 이미지 크기를 반으로 줄이면 더 낮은 차원의 latent 분포를 가진 보다 표현력이 풍부한 생성 모델이 가능하다. 또한 multi-scale 학습은 대규모 이미지를 합성하는 효과적인 전략임이 입증되었다. 따라서 본 논문의 모델은 공간 정보를 점진적으로 추출하여 놀랍도록 사실적인 이미지를 생성한다.

Experiment

1. 2D Toy Example

다음은 다양한 prior에 대하여 MMSE와 3개의 RGM의 복구 밀도를 비교한 것이다.

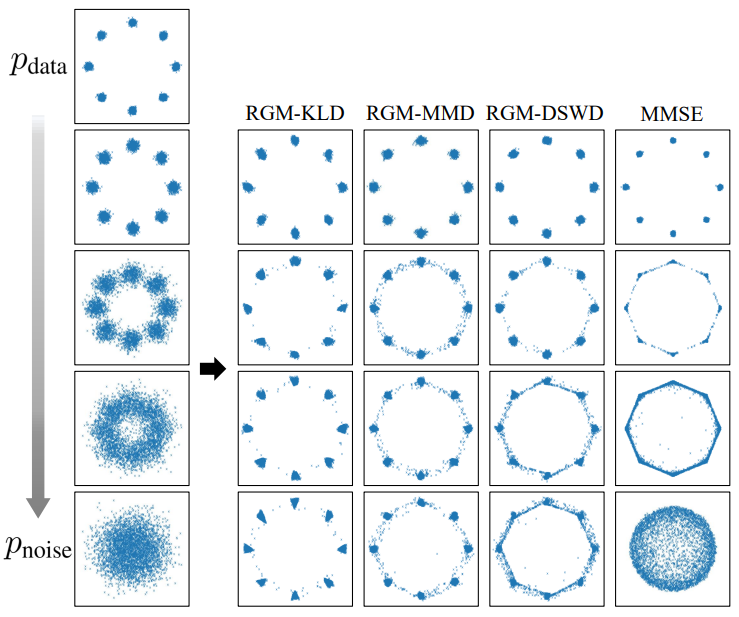
Noise level이 증가함에 따라 MMSE의 실패 정도가 악화된다. MMSE는 noise lebel의 작은 상승에도 불구하고 데이터 분포를 재구성하지 못하기 때문에 MMSE는 적은 수의 diffusion step으로 만족스러운 생성 모델을 생성하지 못한다. 결과적으로 DDM과 같은 MMSE 접근 방식은 데이터 분포를 안정적으로 복구하기 위해 많은 step이 필요하다. 반면에 사전 지식을 추가함으로써 RGM은 multimodal 분포에서 샘플을 훨씬 더 잘 생성하여 MMSE 접근 방식보다 훨씬 적은 수의 forward process로 분포를 복구한다. 이것은 prior term $g$를 사용하는 효과를 보여준다.

RGM은 prior term $g$를 자유롭게 parameterize할 수 있다. RGM 프레임워크가 다양하게 parameterize된 prior term에 대해 보편적으로 작동함을 입증하기 위해 prior term을 KLD, MMD 및 DSWD로 다양하게 설계한다. 위 그림은 세 가지 다른 방식으로 parameterize된 RGM이 일관된 성능을 보여주며 모두 MMSE estimator보다 더 효율적이다. 특히 MMD는 미리 정의된 커널을 기반으로 두 분포 사이의 거리를 측정하므로 $g$는 학습된 것이 아니라 고정되어 있다. 이 간단한 구조에도 불구하고 결과는 MMD가 있는 RGM이 MMSE보다 더 효율적이다.

2. Image Generation

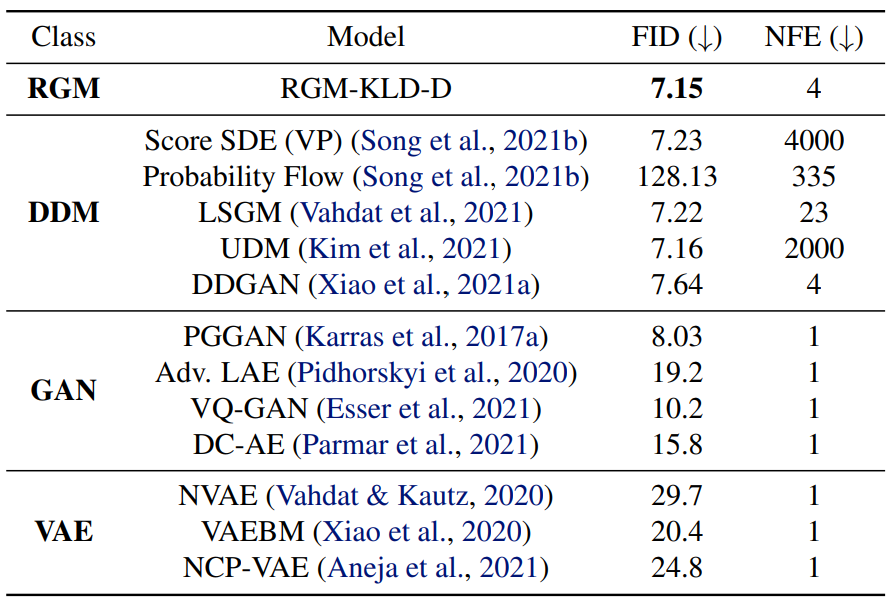
다음은 CIFAR10에서의 unconditional한 생성 결과를 나타낸 표이다. 중간의 “DSWD”와 “KLD”는 사용한 prior term이다. 뒤에 붙은 “D”는 denoising을 의미하고 “SR”은 super-resolution을 의미한다.

다음은 CelebA-HQ-256에서의 생성 결과를 나타낸 표이다.

다음은 LSUN Church(왼쪽)와 CelebA-HQ(오른쪽)에 대하여 생성된 샘플들이다.

다음은 CIFAR10에서 생성된 샘플들이다.

3. Ablation Studies

다음은 다양한 regularization parameter $\lambda$에 대한 FID이다. (Degradation step은 $T = 4$로 고정)

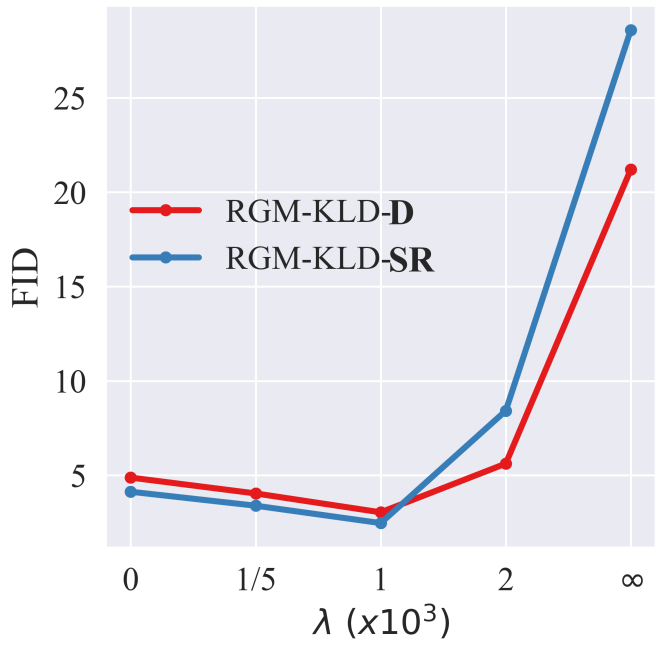
적당한 regularization parameter를 선택하여야 fidelity와 prior term의 균형을 맞출 수 있음을 보여준다.

다음은 CIFAR10에서 RGM들의 ablation study 결과를 나타낸 표이다.

Fidelity term이 없을 때 FID가 저하됨을 보여준다. 특히 RGM-DSWD-D를 보면 여러 timestep을 사용했음에도 불구하고 fidelity term이 없는 성능은 일반 DSWD 모델보다 성능이 나쁘다. 이는 성능 향상이 사전 지식을 설계하는 데 사용한 기존 생성 모델의 힘 때문만은 아니라는 것을 보여준다.

다음은 보조 변수 $z$에 대한 효과를 실험한 것이다.

Noise level이 작으면 재구성이 거의 유일하지만 noise level이 증가하면 $x_k$는 다양한 재구성을 갖는다. 이는 $z$를 할당하는 것이 $z$에서 제공하는 guidance를 통해 심하게 degrade된 $x_k$에서 다양한 denoise된 이미지를 생성하는 데 도움이 된다는 것이 분명하다. 그러나 $z$를 통해서가 아니라 여러 $\sigma_k$를 사용하여 다단계 학습을 하면 ill-posedness가 우회된다고 생각할 수도 있다. 이 주장은 위 표에서 $z$가 없는 RGM-KLD-D의 결과를 사용하여 반박될 수 있다. 동일한 수의 denoising step에서 $z$가 있는 경우와 없는 경우의 RGM-KLD-D의 FID에서 상당한 차이가 관찰되며, 이는 $z$의 유효성을 나타낸다.

Forward process는 데이터와 latent 분포를 연결하는 방법을 결정하기 때문에 모델의 성능에 상당한 영향을 미친다. 위 표에서 $T = 1$일 때 모델을 직접 Gaussian noise에서 데이터 분포로 근사하기 어렵다는 것을 보여준다.

저자들은 SR model의 forward process schedule에 대한 ablation study도 진행하였다. RGM-KLD-SR (naive)와 RGM-KLD-SR을 보면 같은 forward process를 두 단계로 나누는 것이 모델이 학습하기 쉽게 만들어주고 성능 향상을 가져온다는 것을 알 수 있다. 이로부터 forward process를 제대로 설계하면 성능을 크게 향상시킬 수 있음을 알 수 있다.

4. Inverse Problems

RGM은 원래 이미지를 생성하도록 고안되었지만 inverse problem에 적용할 수 있음을 보여준다. 최근 inverse problem를 이미징하는 유망한 접근 방식은 splitting algorithm의 proximal operator에 대한 대안으로 학습된 denoiser를 활용하는 것이다. 이러한 방법론을 Plug-and-Play (PnP) 알고리즘이라고 힌다. 유사하게 다양한 inverse problem를 해결하기 위해 학습된 RGM을 PnP 알고리즘의 modular 부분으로 활용한다. 본 논문에서는 모델을 Douglas-Rachford Splitting algorithm에 연결하여 SR과 colorization에 대해 RGM-KLD-D를 증명하였다.

다음은 LSUN과 CelebA-HQ 데이터셋에서 colorization(왼쪽)과 super-resolution(오른쪽)의 결과이다.

다음은 이미지 복원에 대하여 RGM-KLD-D와 RGM-KLD-SR의 정량적 비교 결과이다.

SR을 기반으로 학습된 RGM-KLD-SR이 실제로 SR task를 더 잘 수행하는 것을 볼 수 있다. 또한 denoising에 대해서도 유사한 경향을 관찰할 수 있다. 결과는 학습에 사용된 degradation process가 실제로 해당 inverse problem를 해결하는 데 실제로 도움이 됨을 확인할 수 있다.