arXiv 2022. [Paper]
Yinhuai Wang, Jiwen Yu, Runyi Yu, Jian Zhang
Peking University Shenzhen Graduate School, Peng Cheng Laboratory
1 Mar 2023

Introduction

Diffusion 기반의 Image Restoration (IR) 방법들은 크게 supervised와 zero-shot으로 나눌 수 있다. 그 중 zero-shot은 방법은 사전 학습된 상용 diffusion model만을 사용하며 finetuning 없이 다양한 IR task를 다룰 수 있기 때문에 새로운 패러다임을 발전시켰다. Zero-shot 방법들이 일반적으로 diffusion model의 선택에 독립적이므로 더 강력한 diffusion model을 사용할 수 있다면 더 좋은 성능을 낼 수 있다. 본 논문에서는 간결하고 유연하고 빠른 zero-shot 방법에 주목하였다.

기존의 diffusion 기반의 IR 방법들은 주로 고정된 출력 크기의 IR 문제에 주목하였다. 하지만 현실에서는 사용자의 요구에 따라 임의의 출력 크기가 필요하다. Zero-shot IR 방법을 임의의 출력 크기에 적용하는 데에는 2가지 어려움이 있다.

  1. Diffusion model이 일반적으로 고정된 크기의 이미지에 대하여 사전 학습되었기 때문에 임의의 크기로 확장하면 out-of-domain (OOD) 문제를 겪는다.
  2. 기본 신경망 구조가 임의의 출력 크기를 지원하지 않느다.

OOD 문제는 랜덤하게 crop된 이미지로 diffusion model을 학습시켜 해결할 수 있다. 하지만 신경망 구조의 제약은 해결하기 어렵다. 이 제약을 피하기 위한 일반적인 방법은 이미지를 고정된 크기의 패치로 나누고 각 패치를 독립적으로 처리한 후 패치들을 연결하여 최종 결과로 사용한다. 하지만, 이 방법은 모든 패치의 글로벌한 semantic을 고려하지 않기 때문에 분명한 블럭 아티팩트와 합리적이지 않은 복구 결과를 만들어 낸다.

저자들은 DDNM이 inpainting task에서 이웃한 패치간의 상관관계가 잘 고려됨을 관찰하였다. 저자들은 DDNM에서 영감을 받아 패치들을 나눌 때 겹치는 영역을 그대로 두고 다음 패치를 처리할 때 겹치는 영역을 추가 마스크 제약 조건으로 사용한다. 이 방법을 Mask Shift Restoration (MSR)이라고 부르며, 패치들 사이의 일관성을 보장하고 효과적으로 경계 아티팩트를 제거한다.

추가로 OOD 문제를 완화하기 위해 먼저 작은 크기에서 결과를 복구한 다음에 이 작은 결과를 글로벌한 사전 지식으로 사용하여 최종 결과를 만든다. 이 방법을 Hierarchical Restoration (HiR)이라 부른다. MSR과 HiR 모두 zero-shot 성질에 완벽하게 맞으며 유연하게 결합할 수 있다. Range-Null space Decomposition (RND) 관점에서 MSR과 HiR은 주어진 inverse problem에 필수적으로 추가 선형 제약들을 추가한다. 이 성질은 DDNM에 완벽하게 알맞으며 RND의 원칙을 정확히 따른다.

Preliminaries

Method

1. Process as a Whole Image

일반적인 diffusion model은 U-Net 구조를 denoise backbone으로 사용한다. 이론적으로 U-Net은 convolutional network이므로 다양한 입력 크기를 지원한다.


따라서 간단한 해결책은 모델 처리 크기를 직접 변경하는 것이다. 유연한 생성 크기를 위해 Stable Diffusion에 유사한 접근 방식이 채택되었다. 유연한 입력 크기를 지원함에도 불구하고 고정 이미지 크기로 학습된 denoiser는 다른 이미지 크기에 적용될 때 OOD 문제에 직면할 수 있다. 위 그림에서 볼 수 있듯이 CelebA 256$\times$256에서 학습된 diffusion model은 512$\times$512 얼굴 이미지를 생성하지 못한다. OOD 문제를 해결하는 한 가지 방법은 256$\times$256 denoise를 정렬된 데이터셋이 아닌 랜덤하게 crop된 데이터셋으로 학습시키는 것이다. 흥미롭게도 ImageNet과 LAION-5B는 정렬되지 않은 데이터셋이므로 상대적으로 사소한 OOD 문제가 발생한다.

2. Process as Patches

모델 처리 크기를 직접 변경하는 것이 작동할 수 있지만 여전히 다음과 같은 제한 사항이 있다.

  1. OOD 문제에 직면했을 때 나쁜 결과를 생성한다.
  2. 여전히 이미지 크기에 제한 사항이 있다. (32로 나눌 수 있어야 함)
  3. 1024$\times$1024와 같은 큰 크기에서 수용할 수 없는 메모리 소비가 발생할 수 있다.
  4. Classifier guidance는 고정된 크기에서 일반적으로 디자인되었으므로 적용할 수 없다.
  5. 다른 backbone (ex. transformer)은 유연한 처리 크기를 지원하지 않을 수 있다.

임의의 이미지 크기를 해결하기 위해 처리 크기가 고정된 diffusion model을 사용할 수 있는 방법은 무엇이 있을까? 간단한 해결책은 입력 이미지 $y$를 패치로 나누고 각 패치를 독립적으로 해결한 다음 결과를 연결하는 것이다. 그러나 이는 분명한 경계 아티팩트를 유발할 수 있다. 이는 각 패치가 독립적으로 해결되고 패치들의 연결이 고려되지 않기 때문이다.

3. Mask-Shift Restoration

많은 IR task 중 inpainting은 마스킹된 영역과 마스킹되지 않은 영역 간의 연결을 고려한 대표적인 작업입니다. DDNM과 RePaint와 같은 zero-shot 방법은 inpainting 해결에 좋은 성능을 보여준다.

저자들의 통찰은 패치를 나눌 때 겹치는 영역을 남겨두고 다음 패치를 해결할 때 이러한 겹치는 영역을 추가 제약 조건으로 사용할 수 있다는 것이다. 멋진 점은 이 제약 조건을 코드 한 줄만 추가하면 기존의 zero-shot 방법에 통합할 수 있다는 것이다.


위 그림과 같은 4$\times$SR task를 생각해보자. 64$\times$96 크기의 입력 이미지 $y^{full}$이 주어지면 256$\times$384 크기의 SR 결과를 얻는 것이 목표이다. Degradation operator $A$를 average-pooling downsampler로 설정하고 $A^\dagger$를 replication upsampler로 설정한다. 위 그림의 (a)는 $A^\dagger y^{full}$의 결과를 보여준다. 먼저 $A^\dagger y^{full}$를 256$\times$256 크기의 두 개의 패치 $A^\dagger \dot{y}$와 $A^\dagger y$로 나눈다. 두 패치는 256$\times$128 크기만큼 겹친다.

먼저 기본 DDNM을 $A^\dagger \dot{y}$에 사용하여 SR 결과 $\dot{x}_0$를 얻는다 (위 그림의 Step 1). 두 패치의 겹치는 영역은 이미 $\dot{x}_0$에 복구되었다. 그런 다음 $A^\dagger y$를 DDNM을 복구할 때 복구된 겹쳐진 영역을 inpainting에서 알고 있는 영역으로 설정한다. DDNM의 식에 다음과 같은 추가 inpainting 제약 조건을 추가한다.

\[\begin{equation} \bar{x}_{0 \vert t} = A_m \dot{x}_0 + (I - A_m) \hat{x}_{0 \vert t} \end{equation}\]

$A_m$은 겹쳐진 영역에 대한 mask operator이다. 전체 알고리즘은 Algorithm 2와 같으며 Mask-Shift Restoration (MSR)이라 부른다.


위 그림의 (c)에서 볼 수 있듯이 Step 1과 Step 2의 결과를 concat한 최종 결과가 경계 아티팩트를 보이지 않는다는 것을 알 수 있다. 비슷하게, MSR을 반복적으로 사용하여 무제한 크기의 이미지를 생성하는 데 사용할 수 있으며, 경계 아티팩트가 생기지 않는다. 겹친 영역과 shift하는 방향은 임의로 정할 수 있으며, SR뿐만 아니라 다른 linear inverse problem에도 사용할 수 있다.

4. Hierarchical Restoration


MSR은 로컬 일관성을 보장하지만 큰 이미지를 처리할 때 작은 receptive field를 가진다. 이로 인해 글로벌한 정보에 대한 이해가 부족하여 semantic 정보 복구가 잘못될 수 있다. 위 그림의 (a)에서 크기 512$\times$768의 마스킹된 이미지를 보여준다. 여기서 256$\times$256 패치는 전체 semantic 주제를 커버할 수 없다. 위 그림의 (b)는 DDNM 기반의 MSR을 사용한 결과이다. 로컬 일관성은 우수하지만 합리적이지 않은 semantic 구조를 생성한다.

본 논문은 receptive field를 확장하기 위해 Hierarchical Restoration (HiR)을 제안하며, 이를 통해 더 나은 semantic 복원을 달성한다. HiR은 semantic 복원 단계와 texture 복원 단계의 두 단계로 구성된다.

위 그림의 (a)를 예로 들면, semantic 복원 단계에서 먼저 2$\times$ downsample를 하여 512$\times$768 입력을 256$\times$384로 변환한다. 그런 다음 256$\times$256 크기의 패치로 DDNM 기반의 MSR을 사용하여 256$\times$384 크기의 inpainting 결과 $\ddot{x}_0$를 얻는다. 그 결과는 아래 그림의 (a)와 같다.


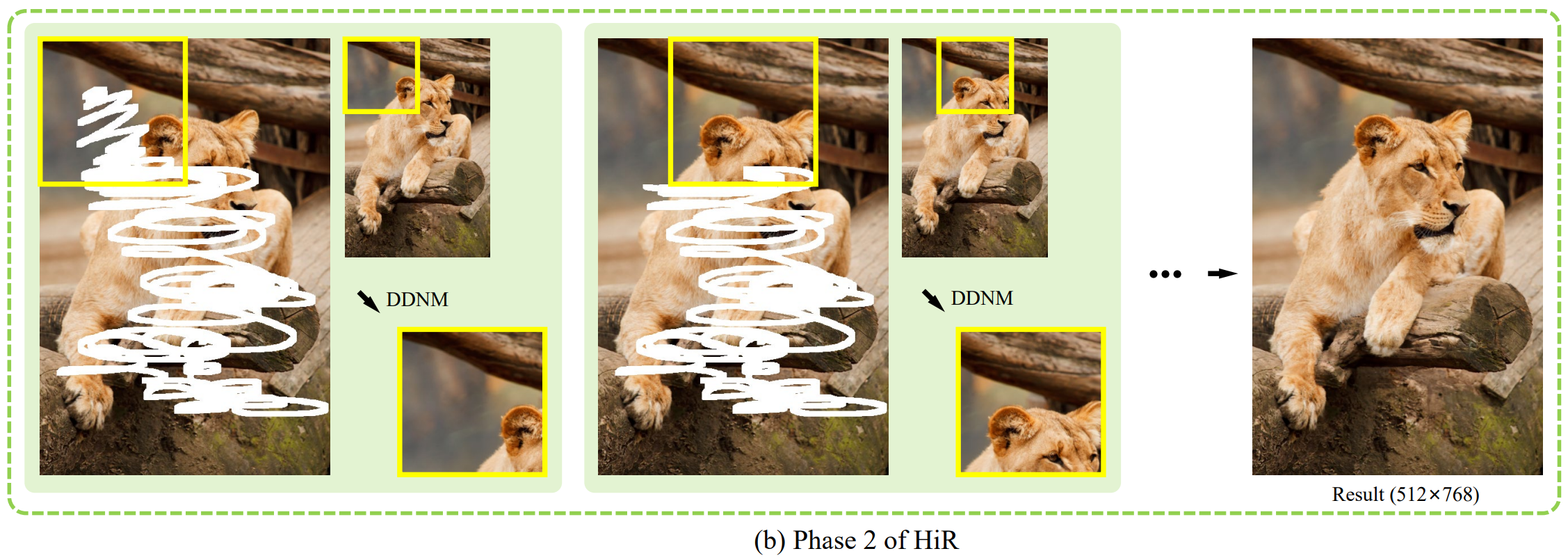
이 결과는 semantic하게 합리적이고 저주파수 레퍼런스로 사용될 수 있다. Texture 복원 단계 (위 그림의 (b))에서는 다음과 같은 저주파수 제약 조건을 추가한다.

\[\begin{equation} \tilde{x}_{0 \vert t} = A_\textrm{sr}^\dagger \ddot{x}_0 + (I - A_\textrm{sr}^\dagger A_\textrm{sr}) x_{0 \vert t} \end{equation}\]

$A_\textrm{sr}$는 average-pooling downsampler이고 $A_\textrm{sr}^\dagger$는 $A_\textrm{sr}$의 pseudo-inverse upsampler이다. Algorithm 3는 HiR의 두번째 단계의 전체 알고리즘을 보여준다.


HiR은 inpainting task뿐만 아니라 큰 규모의 SR이나 colorization에도 사용할 수 있다.

5. Flexible Pipeline for Applications

MSR은 일반적인 패치 연결 테크닉으로 볼 수 있으며 HiR은 복원 품질을 향상시키는 일반적인 방법으로 볼 수 있다. MSR과 HiR의 본질은 해 공간을 좁히기 위해 사전 지식을 통해 정보의 일부를 결정하는 것이다. 본 논문에서는 간결하고 효과적이며 수학적으로 우아한 Range-Null space Decomposition을 통해 MSR과 HiR을 구현한다. 게다가 MSR과 HiR을 구현하는 다른 가능한 방법이 남아 있다 (ex.: DPS와 같은 최적화 기반 방법에 loss 추가). 따라서 제안된 MSR과 HiR은 ILVR, RePaint, DPS와 같은 다른 diffusion 기반 zero-shot IR 방법에도 사용할 수 있다.

Experiment

  • 모든 실험에서 ImageNet 256$\times$256에서 사전 학습된 denoiser 사용
  • 샘플링 시 classifier guidance 사용
  • 시간 여행 트릭을 사용하여 생성 품질 개선
  • 왼쪽에서 오른쪽으로, 위에서 아래로 패치로 나눔
  • 각 패치는 256$\times$256 크기이고, 경계를 제외하고 128 픽셀만큼 겹침
  • 첫번째 패치는 오리지널 DDNM으로 풀고 나머지 패치들은 DDNM 기반의 MSR을 사용

다음은 noisy 4$\times$SR에 대한 실험 결과를 BSRGAN과 비교한 것이다.


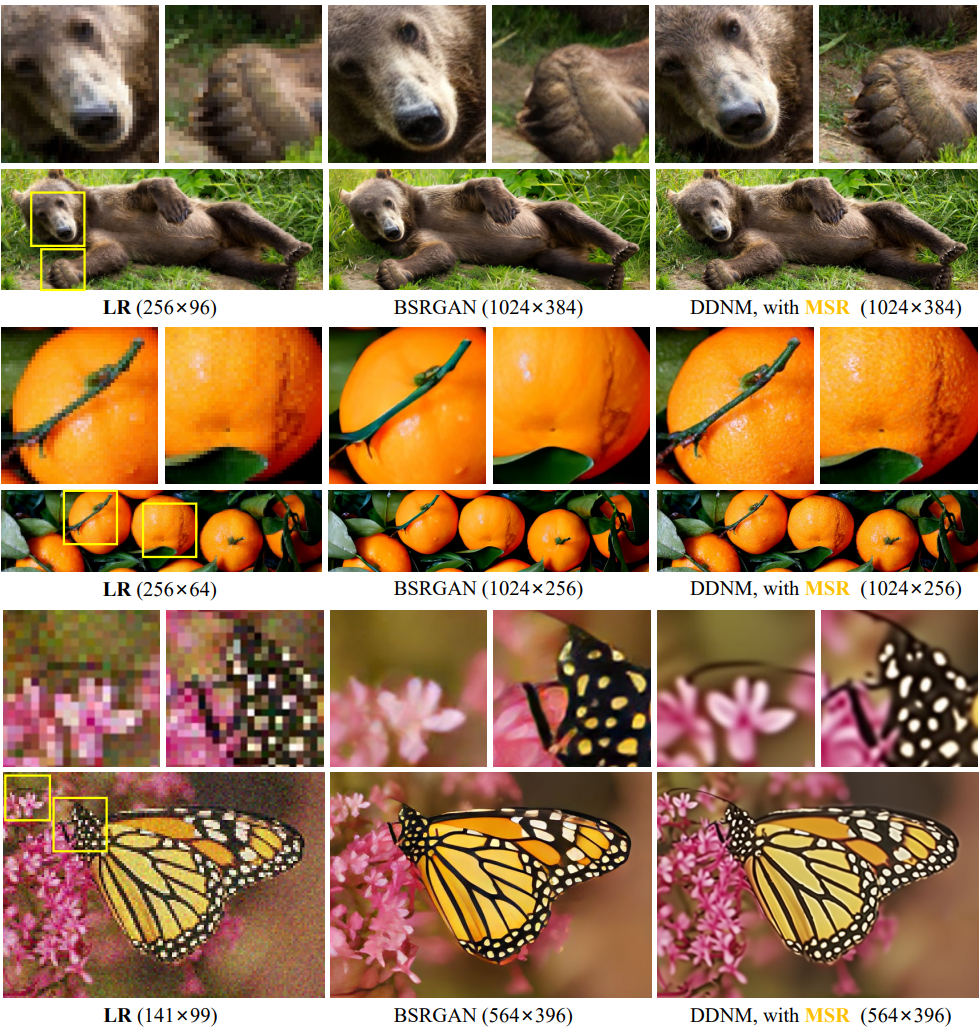
본 논문의 방법이 현실성과 일관성 모두에서 더 좋은 성능을 보였으며, RND의 사용으로 낮은 해상도에서 정확한 색과 구조 정보를 충실히 상속할 수 있다.

다음은 HiR을 사용한 colorization 결과이다.

Limitations

  1. 널리 사용되는 supervised 방법보다 계산과 시간 소비가 훨씬 더 많다.
  2. 성능 상한선은 사전 학습된 diffusion model에 따라 다르다.
  3. Stable Diffusion과 같이 latent space를 기반으로 하는 모델은 zero-shot 방법을 적용하기 어렵다.
  4. Degradation operator이 명시적으로 필요하므로 비나 안개 제거와 같은 task는 어렵다.