arXiv 2022. [Paper]
Hongkai Zheng, Weili Nie, Arash Vahdat, Kamyar Azizzadenesheli, Anima Anandkumar
Caltech | NVIDIA
24 Nov 2022
Introduction
Diffusion model의 빠른 샘플링을 위한 기존 방법은 학습 없는 샘플링 방법과 학습 기반 샘플링 방법의 두 가지로 요약할 수 있다. 특히 학습이 필요 없는 방법은 SDE 또는 probability flow ODE를 풀면서 수치적 관점에서 이산화 step 수를 줄이는 데 중점을 둔다. 그러나 가장 잘 설계된 numerical solver도 수용 가능한 샘플링 품질을 위해 근사 오차가 충분히 작도록 하려면 여전히 10~30개의 모델 평가가 필요하다. 반면에 학습 기반 방법은 numerical solver의 일부 또는 전체를 대체하기 위해 대리 네트워크를 학습시킨다. 특히 progressive distillation은 실시간 샘플링을 향한 큰 진전을 이루었지만 여전히 기존의 numerical solver와 같은 순차적 특성을 가지고 있다.
본 논문의 목표는 단 하나의 모델 평가로 diffusion model에 대한 빠르고 병렬인 샘플링 방법을 개발하는 것이다. 궤적의 서로 다른 시간 위치에서 이미지를 병렬로 디코딩할 수 있으므로 하나의 모델 평가만 사용하여 최종 솔루션을 생성할 수 있다. 여기서 주요 과제는 일반적으로 수치적 근사 관점에서 정확하게 흉내내기 위해 많은 이산 timestep이 필요한 복잡하고 큰 규모의 미분 방정식을 푸는 어려움에서 발생한다.
본 논문에서는 이 문제를 극복하기 위해 미분 방정식을 푸는 데 사용되는 neural operator의 최근 발전을 사용한다. Neural operator, 특히 Fourier neural operator (FNO)는 기존 solver보다 몇 배 더 빠르다. 이 모델 클래스는 함수 공간 사이의 매핑을 학습하고 이산화 불변으로 표시되어 모델 파라미터를 변경하지 않고 데이터를 다른 해상도에서 작업할 수 있도록 하며 주어진 비선형 연속 operator를 근사화할 수 있다.
FNO는 병렬 디코딩을 허용한다. 즉, 궤적의 모든 위치에서 출력을 동시에 평가할 수 있다. 이것은 diffusion model에 대한 이전 샘플링 방법 중 어느 것도 누리지 못하는 속성이다. 본 논문에서는 초기 조건(즉, 가우시안 분포)을 해의 궤적에 매핑하는 neural operator for diffusion model sampling (DSNO)를 제안하고 unconditional 및 클래스 조건부 이미지 생성 모두에서 그 효과를 보여준다.
Background
Score-based generative models
통합된 연속 시간 프레임워크에서 score 기반 생성 모델의 일반적인 클래스를 고려한다. 본 논문에서는 score 기반 모델과 diffusion model을 혼용하여 사용한다. 데이터 분포가 $p_\textrm{data}$라고 가정하면, forward pass는 0에서 $T$까지의 diffusion process \(\{x(t)\}\)는 다음과 같이 표현된다.
\[\begin{equation} dx = f(x, t) dt + g(t) dw_t \end{equation}\]$w_t$는 standard Wiener process이고, $f$와 $g$는 각각 drift 계수와 diffusion 계수이다. Diffusion model은 $x(0) \sim p_\textrm{data}$와 $x(T) \sim \mathcal{N}(0,I)$을 만족하는 $f$와 $g$를 선택한다. 다음과 같은 probability flow ODE는 diffusion process와 같은 주변 분포 $p_t (x)$를 생성한다.
\[\begin{equation} dx = f(x, t)dt - \frac{1}{2} g(t)^2 \nabla_x \log p_t (x) dt \end{equation}\]초기 조건 $x(T)$가 주어지면 $T$에서 0까지의 probability flow ODE를 풀어 sampling process를 얻을 수 있다. 또한 $f(x, t) = h(t) x$와 같이 affine form으로 두면 probability flow ODE 식이 semi-linear ODE로 간단하게 바뀐다.
\[\begin{equation} x(t) = \phi (t, s) x(s) - \int_s^t \phi (t, \tau) \frac{g(\tau)^2}{2} \nabla_x \log p_\tau (x) d \tau \\ \phi (t, s) = \exp (\int_s^t h(\tau) d \tau) \end{equation}\]ODE는 numerical solver로 풀 수 있다. Score fuction $\nabla_x \log p_t (x)$는 보통
\[\begin{equation} \hat{\epsilon}_\theta (x_t) \approx - \sigma_t \nabla_x \log p_t (x) \end{equation}\]으로 parameterize하며, 여기서 $\sigma_t$는 noise schedule이다.
Fourier neural operator
Fourier neural operator는 PDE를 푸는 state-of-the-art 데이터 기반 방법중 하나이며, 데이터에서 두 개의 Banach 공간 사이의 parametric map을 학습하여 많은 과학 문제에서 기존 PDE solver보다 뛰어난 속도 향상을 보였다. 이들을 커널 함수가 학습 가능한 가중치로 parameterize되는 커널 통합 layer의 스택으로 구성된다.
$D$를 제한된 도메인이라고 하고 (ex. $[0, T]$) $a : D \rightarrow \mathbb{R}^{d_\textrm{in}}$을 입력 함수라 하자. Fourier neural operator $\mathcal{G}_\theta$는 다음과 같은 형태의 $L$개의 layer를 가진 neural operator이다.
\[\begin{equation} \mathcal{G}_\theta := \mathcal{Q} \circ \sigma (\mathcal{W}_L + \mathcal{K}_L) \circ \cdots \circ \sigma (\mathcal{W}_1 + \mathcal{K}_1) \circ \mathcal{P} \end{equation}\]여기서 $\mathcal{P}$는 lifting 연산자, $\mathcal{Q}$는 projection 연산자, $\mathcal{W}_i$는 residual 연결이다. $\mathcal{K}$는 Fourier space에서 parameterize된 적분 커널 연산자이며, 주어진 $v_i$에 대하여 $i$번째 레이어에 대한 입력 함수는 다음과 같다.
\[\begin{equation} (\mathcal{K} v_i) (t) = \mathcal{F}^{-1} (R_i \cdot (\mathcal{F} v_i)) (t), \forall t \in D \end{equation}\]$\mathcal{F}$는 푸리에 변환, $\mathcal{F}^{-1}$는 푸리에 역변환이고, $D$와 $R_i$는 학습 가능한 파라미터이다.
입력 함수 $a$가 주어지면 $a$의 여차원(co-dimension)을 $\mathcal{P}$로 확장하고, $L$개의 전역 적분 연산자를 통과시킨다. 그 출력을 $\mathcal{Q}$에 통과시켜 출력 함수를 계산한다. 이 아키텍처는 중요한 이산화 불변성과 범용 연산자의 범용 근사 속성을 보유한다.
Learning the trajectory with neural operator
Problem statement
본 논문의 목표는 초기 조건 $x(T) \sim \mathcal{N}(0,I)$이 주어지면 종점 $x(0) \in \mathbb{R}^d$가 데이터인 probability flow trajectory \(\{x(t)\}_s^0\)을 예측하는 neural operator를 학습시키는 것이다. $D = [0, s]$를 시간 도메인이라고 하자. 그리고 $\mathcal{A}$를 초기 조건의 유한 차원 space, $\mathcal{U} = \mathcal{U} (D; \mathbb{R}^d)$를 타겟 연속 시간 함수의 space라고 하자.
Neural operator $\mathcal{G}_\theta$는 다음과 같은 오차를 최소화하여 solution operator $\mathcal{G}^\dagger$를 근사하도록 구축한다.
\[\begin{equation} min_\theta \mathbb{E}_{x_T \sim \mathcal{N}(0,I)} \mathcal{L} (\mathcal{G}_\theta (x_T) - \mathcal{G}^\dagger (x_T)) \end{equation}\]$\mathcal{L}$은 $L^p$ norm과 같은 손실 함수이다. Exact solution $x(t)$에서 solution operator $\mathcal{G}^\dagger : \mathcal{A} \rightarrow \mathcal{U}$가 존재하고 score 함수의 고유한 가중 적분 연산자이다. 즉, solution operator는 diffusion ODE에 해당하며, $x(T)$를 probability flow trajectory \(\{x(t)\}_s^0\)으로 매핑한다. 이 operator는 근사가 가능한 neural operator 집합에 포함되는 일반 operator이다.
즉, 제안된 아키텍처는 하나의 모델 호출에서 \(\{x(t)\}_s^0\)를 출력하는 방법을 학습하는 데 필요한 capacity를 가지고 있다.
Temporal convolution block in Fourier space
Exact ODE solution의 가중 적분 형태에서 영감을 받아 본 논문은 푸리에 적분 연산자 $\mathcal{K}$를 가지는 temporal convolution block을 만들어 궤적을 효율적으로 모델링한다. 입력 함수 $u : \mathcal{D} \rightarrow \mathcal{R}^d$가 주어지면 temporal convolution layer $\mathcal{T}$는 다음과 같이 정의된다.
\[\begin{equation} (\mathcal{T} u) (t) = u(t) + \sigma ((\mathcal{K} u) (t)) \end{equation}\]$\sigma$는 point-wise 비선형 함수이고, $\mathcal{K}$는 $R$로 parameterize된 푸리에 convolution 연산자이다. 제안된 $\mathcal{T}$가 FNO layer와 조금 다르다는 것을 알 수 있다.
구체적으로, 비선형 활성화 함수를 $\mathcal{K}$ 앞에 위치시키고 선형 연산자 $\mathcal{W}$를 identity shortcut으로 교체하여 추가 비용 없이 고주파수 정보를 보존하고 더 나은 최적화를 이끈다. 저자들은 일반적인 선형 layer를 사용하는 이점을 관찰하지 못했다고 한다. Identity map은 계산적으로 효율적이기 때문에 충분하고 더 매력적이다. 또한, convolution 정리에 따라 다음이 성립한다.
\[\begin{equation} (\mathcal{K} u) (t) = \int_D (\mathcal{F}^{-1} R) (\tau) u(t - \tau) d \tau, \forall t \in D \end{equation}\]위 식에서 적분 형태는 diffusion process와 구조적인 유사성을 가지고 있으며, 이는 temporal convolution layer가 ODE solution trajectory를 parameterize함을 뜻한다.
실제로는 계산 효율성을 위해 이산 푸리에 변환을 사용한다. 시간 도메인 $D$가 $M$개의 점으로 이산화된다고 하자. 이해를 쉽게 하기 위해, 입력의 여차원과 temporal convolution block의 출력 함수가 모두 $\mathbb{R}^d$라고 하자. 입력 함수 $u(t)$는 텐서 $\mathbb{R}^{M \times d}$이고, $R$은 복소수 값을 갖는 파라미터 $\mathbb{C}^{J \times d \times d}$이다. $J$는 선택할 수 있는 모드의 최대 개수다.
모든 $u$에 대하여 $J$보다 큰 모드를 자른 다음 $\mathcal{F} (u) \in \mathbb{C}^{J \times d}$를 얻는다. 입력의 푸리에 변환과 커널 함수의 pointwise product는 다음과 같다.
\[\begin{equation} R \cdot (\mathcal{F} u)_{j, k} = \sum_{l=1}^d R_{j, k, l} (\mathcal{F} u)_{j, l} \end{equation}\]따라서 $\mathcal{F}$와 $\mathcal{F}^{-1}$은 FFT 알고리즘으로 구현할 수 있다.
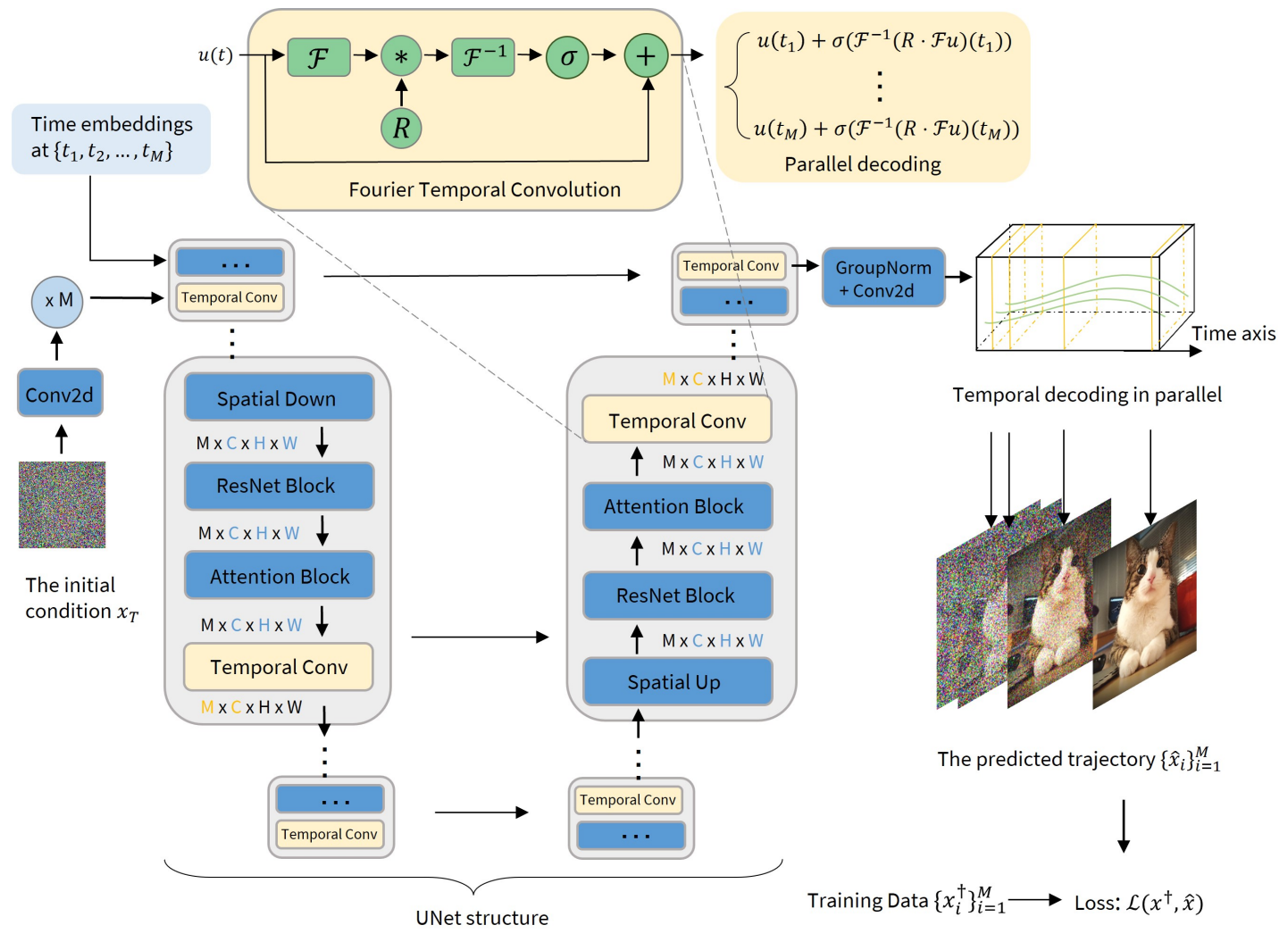
위 그림은 temporal convolution layer의 구현 디테일을 보여준다. Temporal convolution layer는 시간 차원과 채널 차원에 대해서만 연산하며, 따라서 픽셀 차원을 배치 차원과 동일하게 취급한다. 즉, 위의 예시에서의 $d$는 실제로 채널 차원의 수에 해당한다.
Architecture of DSNO
위 그림에서와 같이 DSNO의 아키텍처는 어떠한 기존 diffusion model 아키텍처의 위에 구축할 수 있으며, 이는 U-Net 아키텍처의 각 레벨에 temporal convolution layer를 추가하면 된다.
위 그림에서 파란색 블럭은 기존 diffusion model backbone의 모듈이며 시간 차원을 배치 차원으로 취급하여 픽셀과 채널 차원에서만 작동한다. 노란 블럭은 Fourier temporal convolution block으로 시간과 채널 차원에서만 작동한다. 따라서, 본 논문의 모델은 굉장히 병렬화할 수 있으며 원래 backbone에 최소한의 계산 복잡성을 추가한다.
시간 차원이 \(\{t_1, \cdots, t_M\}\)으로 이산화되다고 가장하면, DSNO는 이 시간들에 대한 time embedding과 초기 조건을 입력으로 받는다. 첫번째 convolution layer의 feature map은 $M$번 시간 차원에서 반복되어 서로 다른 시간에서의 초기 feature가 된다. 각 feature 표현은 time embedding과 합쳐진 후 다음 ResNet block에 입력된다.
Training of DSNO
DSNO 학습은 표준 연산자 학습 세팅과 같다. 목적 함수는 오차의 가중 적분이다.
\[\begin{equation} \min_\theta \mathbb{E}_{x_T \sim \mathcal{N}(0,I)} \int_D \lambda (t) \| \mathcal{G}_\theta (x_T) (t) - \mathcal{G}^\dagger (x_T) (t) \| dt \end{equation}\]$\theta$는 DSNO의 파라미터이고 $\lambda (t)$는 가중치 함수이며 $x_T$는 초기 조건이다. 실제로는 empirical-risk를 최소하여 $\theta$를 최적화한다.
\[\begin{equation} \min_\theta \frac{1}{N} \sum_{j=1}^N \frac{1}{M} \sum_{i=1}^M \lambda (t_i) \| \mathcal{G}_\theta (x_T^{(j)})(t_i) - \mathcal{G}^\dagger (x_T^{(j)}) (t_i) \| \end{equation}\]어떠한 solver나 샘플링 방법을 사용하여 $\mathcal{G}^\dagger (x_T^{(j)}) (t_i)$를 생성해도 된다.
Parallel decoding
위 그림의 위의 두 노란 블럭을 보면 Fourier temporal convolution block이 서로 다른 시간의 이미지를 병렬로 예측하는 것을 볼 수 있다. 임의의 입력 함수 $u(t)$가 주어지면 푸리에 계수 $R \cdot \mathcal{F} u$를 계산한 다음 푸리에 역변환을 모든 $t_i$에서 병렬로 실행하여 서로 다른 시간의 출력을 한 번에 생성할 수 있다. 또한, DSNO의 다른 모듈들은 시간 차원을 배치 차원으로 취급하므로 모든 $t_i$에 대하여 병렬로 연산을 수행할 수 있다. 따라서 DSNO는 효율적인 병렬 디코딩이 가능하다.
본 논문의 병렬 디코딩의 유효성은 diffusion ODE의 해에 기반하며 주어진 조건에 조건부로 독립적이다. 병렬 디코딩은 동간 차원에서의 이산 토큰 생성을 위한 transformer 기반 모델이나 언어 모델에서 유효성을 보여주었다. DSNO는 연속적인 diffusion ODE 궤적을 위한 첫 병렬 디코딩 방법이다.
Compact power spectrum
저자들은 다양한 사전 학습된 diffusion model로 생성한 probability flow ODE 궤적의 스펙트럼을 확인해 보았으며 ODE 궤적이 항상 시간 차원에 대해 컴팩트한 에너지 스펙트럼을 가지는 것을 확인했다. Diffusion ODE 궤적의 매끄러움은 고주파수 모드들이 목적 함수에 적게 기여한다는 것을 의미한다. 따라서 DSNO는 diffusion ODE들의 solution operator를 상대적으로 작은 이산화 step $M$을 사용하여 더 효율적으로 모델링할 수 있다.
Experiments
- 증류시킬 사전 학습된 diffusion model을 사용하여 ODE 궤적들의 학습셋을 랜덤하게 샘플링하고, 그런 다음 diffusion model에 간단하게 temporal convolution layer를 더해 DSNO를 위한 backbone을 만듬
- 기존 아키텍처의 모듈은 사전 학습된 가중치로 초기화
- Temporal convolution layer의 활성화 함수 $\sigma$로는 LeakyReLU를 사용
- 모든 실험에서 목적 함수에는 $L^1$-norm을 사용
- Loss 가중치 함수로 $\lambda (t) = \alpha_t / \sigma_t$를 사용 (원래 diffusion model에서 사용되는 SNR 가중치의 제곱근)
- Batch size: CIFAR-10에서는 256, ImageNet에서는 2048, ablation study에서는 128
- Learning rate (0.0002), warmup schedule, Adam optimizer의 $\beta_1, \beta_2$ 모두 diffusion model의 hyperparameter 그대로 사용
다음은 V100에서 모델 평가 비용을 테스트한 표이다.
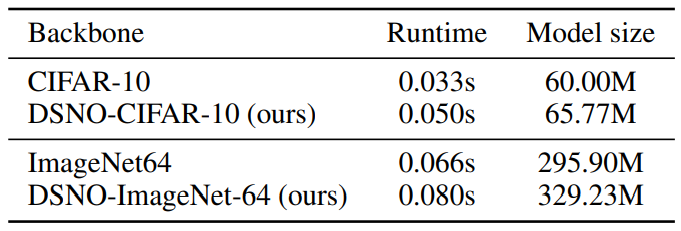
1. Unconditional generation: CIFAR-10
다음은 CIFAR-10에서의 빠른 샘플링 방법들을 비교한 표이다.
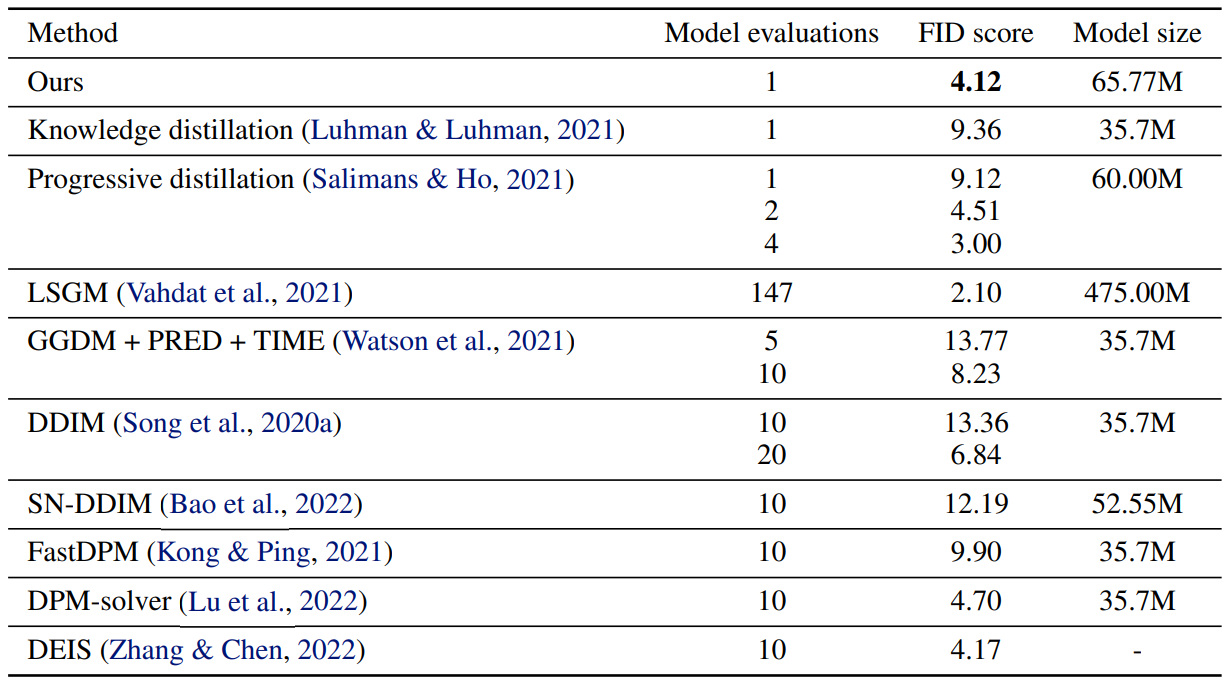
DSNO는 4-step progressive distillation model보다 2.6배 빠르며, 2-step보다는 1.3배 빨랐다고 한다. 원본 diffusion model의 아키텍처에 비해 파라미터는 10%보다 적게 증가하였다고 한다.
2. Conditional generation: ImageNet-64
다음은 클래스 조건부 ImageNet-64에서 빠른 샘플링 방법들을 비교한 표이다.

DSNO는 2-step progressive distillation model보다 1.7배 빨랐다고 하며, 원본 아키텍처와 비교했을 떄 파라미터가 10%정도 증가하였다고 한다.
다음은 DSNO로 예측된 궤적과 원래 ODE solver의 궤적을 고정된 random seed에서 시간 해상도 4로 비교한 것이다.

DSNO가 예측한 궤적이 ground-truth ODE 궤적과 굉장히 일치하며 DSNO의 병렬 디코딩 유효성을 보여준다.
다음은 같은 random seed에서 사전 학습된 원본 diffusion model과 DSNO의 랜덤 샘플이다.
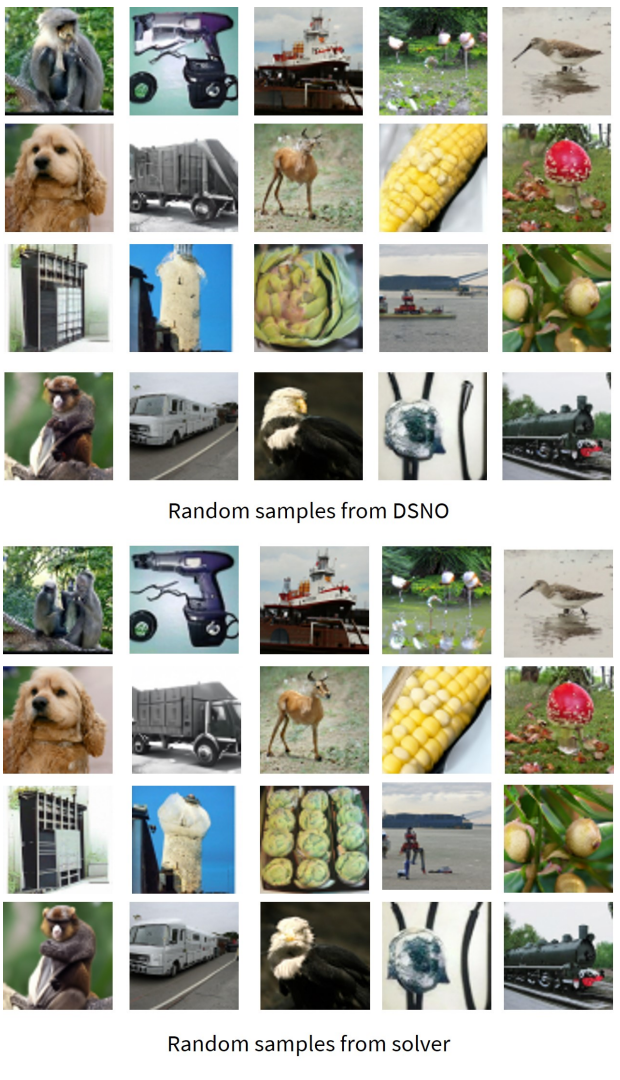
Gaussian noise에서 출력 이미지로의 매핑이 잘 보존된다는 것을 알 수 있다.
4. Ablation study
Loss weighting
다음은 loss weighting과 시간 이산화 방법에 대한 ablation study 결과를 나타낸 표이다.

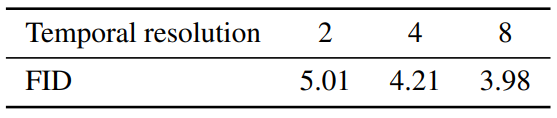
다음은 시간 해상도에 대한 ablation study 결과를 나타낸 표이다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)