ISMIR 2021. [Paper] [Github]
Gautam Mittal, Jesse Engel, Curtis Hawthorne, Ian Simon
University of California, Berkeley | Google Brain
30 Mar 2021
Introduction
DDPM은 데이터에서 가우시안 noise로의 diffusion process를 반전시키는 방법을 학습하여 비교적 고품질 샘플을 합성할 수 있는 새로운 종류의 생성 모델이다. DDPM은 Langevin 역학에서 영감을 받은 반복적 개선 프로세스를 통해 샘플링하며, unconditional하게 학습된 모델에 사후 컨디셔닝이 가능하다.
이러한 흥미로운 발전에도 불구하고 DDPM은 샘플링 프로세스가 이미지나 오디오와 같은 연속적인 영역에 국한되기 때문에 아직 symbolic music 생성에 적용되지 않았다. 마찬가지로 DDPM은 별도의 하위 레벨 오토인코더에서 추출한 개별 토큰을 모델링하는 2단계 프로세스를 사용하는 long-term 모델링의 최근 발전을 활용할 수 없다.
본 논문에서는 긴 형식의 discrete symbolic music을 생성하기 위해 low-level variational autoencoder (VAE)의 연속 latent에서 DDPM을 학습시킴으로써 이러한 한계를 극복할 수 있음을 보여준다.
Model

1. Architecture
본 논문의 모델은 먼저 파라미터 $\gamma$를 사용하여 VAE를 학습시킨 다음, $k$ VAE latnet 사이의 시간적 관계를 캡처하도록 diffusion model을 학습시켜 MIDI의 discrete 시퀀스를 생성하는 방법을 학습한다. MusicVAE와 같은 시퀀스 VAE는 긴 시퀀스에서 학습하기 어렵다. 이를 극복하기 위해 짧은 2마디 MusicVAE 모델을 $k = 32$ latent 사이의 종속성을 모델링할 수 있는 diffusion model과 페어링하여 총 64개의 마디(bar)를 모델링한다.
MusicVAE embeddings
각 악구(phrase)는 소절(measure)당 16개의 양자화된 step이 있는 일련의 one-hot vector이며, vocabulary에는 90개의 토큰(1 note on + 1 note off + 88 pitches)이 포함된다. 그런 다음 사전 학습된 2마디 멜로디 MusicVAE를 사용하여 각 2마디 소절을 parameterize하고, 전체 시퀀스를 parameterize하기 위해 연속 latent embedding 시퀀스 $z_1, \cdots, z_k$를 생성한다.
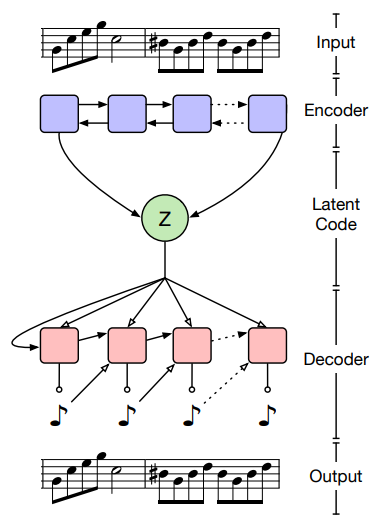
MusicVAE 모델은 위 그림에 표시된 대로 양방향 LSTM을 인코더로 사용하고 autoregressive LSTM을 디코더로 사용한다. 각 2소절 악구를 latent $z$ embedding으로 인코딩한 후 각 embedding의 도메인이 $[-1, 1]$이도록 선형 스케일링을 수행한다. 이렇게 하면 diffusion model에 대한 isotropic Gaussian latent $x_N$에서 시작하여 일관되게 스케일링된 입력이 보장된다.
Transformer diffusion model
신경망 $\epsilon_\theta (x_t, \sqrt{\vphantom{1} \bar{\alpha}_t}) : \mathbb{R}^{k \times 42} \times \mathbb{R} \rightarrow \mathbb{R}^{k \times 42}$은 transformer이며, $k = 32$는 각 전처리된 42차원 latent embedding 시퀀스의 길이이다. Diffusion model을 학습시키는 데 사용되는 원본 데이터 분포는 $x_0 = [z_1, \cdots, z_k]$이다. 신경망은 맨 처음에 embedding을 128차원 space로 projection하는 fully-connected (FC) layer를 가지며, 그 다음에 각각 self-attention head 8개와 residual FC layer로 구성된 $L = 6$인 인코더 layer를 가진다. 모든 self-attention과 FC layer는 layer normalization을 사용한다. 인코더의 출력은 reverse process 출력을 생성하는 $K = 2$ noise-conditioned residual FC layer에 입력된다. 각 FC layer는 2048개의 뉴런을 가진다. 또한 다음과 같은 128차원 sinusoidal 위치 인코딩을 사용한다.
\[\begin{equation} \omega = [10^{\frac{-4 \times 0}{63}} j, \cdots, 10^{\frac{-4 \times 63}{63}} j] \\ e_j = [\sin (\omega), \cos (\omega)] \end{equation}\]여기서 $j$는 latent input embedding의 위치 인덱스다. Positional encoding $e_1, \cdots, e_k$는 transformer 인코더 layer에 입력되기 전에 $x_t$에 더해지며, 이를 통해 모델이 입력의 시간적 컨텍스트를 캡처하도록 한다.
Noise schedule and conditioning
원래 diffusion model 프레임워크에 설명된 대로 추가 sinusoidal encoding을 사용하여 학습과 샘플링 중에 diffusion model을 연속 noise 레벨로 컨디셔닝한다. 이 noise 인코딩은 위에서 설명한 위치 인코딩과 동일하지만 업데이트된 도메인을 설명하기 위해 각 sinusoid의 주파수를 5000으로 스케일링한다. Feature-wise linear modulation을 사용하여 noise 인코딩이 주어진 $\gamma$(scale)와 $\xi$(shift) 파라미터를 생성하고 transformation $\gamma \phi + \xi$를 각 residual layer의 각 layer normalization block의 출력 $\phi$에 적용하여 diffusion model의 효과적인 컨디셔닝이 가능하다. 본 논문의 모델은 $N = 1000$, $\beta_1 = 10^{-6}$, $\beta_N = 0.01$인 linear noise schedule을 사용한다.
2. Unconditional Generation
Unconditional 생성 task에서 목표는 long-term 구조를 나타내는 샘플을 생성하는 것이다. 본 논문의 multi-stage 접근 방식 덕분에 diffusion model이 latent space의 구조를 정확하게 캡처하여 샘플 품질을 향상시키므로 posterior $q_\gamma (z)$와 Gaussian prior 사이의 KL divergence가 상당히 큰 경우에서도 작동한다. 또한 diffusion model을 사용하여 latent embedding의 시퀀스를 예측하고 많은 소절에서 일관된 패턴으로 unconditional한 샘플을 생성하도록 학습된 것보다 더 길게 샘플링하도록 기본 VAE를 확장한다.
3. Infilling
Noise를 데이터 샘플로 반복적으로 정제하는 샘플링 프로세스를 사용하는 이점 중 하나는 diffusion model을 재학습할 필요 없이 reverse process의 궤적을 조정하고 임의로 컨디셔닝할 수 있다는 것이다. 창의적 측면에서 이 사후 컨디셔닝은 새로운 task를 위해 모델을 수정하거나 재학습할 리소스가 없는 아티스트에게 특히 유용하다. Unconditional하게 학습된 diffusion model을 사용하여 latent embedding의 조건부 infilling으로 음악에 적용되는 diffusion modeling의 힘을 보여준다.
Infilling 절차는 부분적으로 가려진 샘플 $s$의 정보를 통합하여 샘플링 절차를 확장한다. 샘플링의 각 step에서 $s$의 고정된 영역을 forward process로 diffuse하고 mask $m$을 사용하여 업데이트된 샘플 $x_{t-1}$에 diffuse된 고정 영역을 추가한다. 최종 출력은 $s$의 가려진 영역이 reverse process로 inpainting된 버전이다.
이 수정된 샘플링 절차는 Algorithm 1과 같다.

Experiments
- 데이터셋
- Lakh MIDI Dataset (LMD) (17만 개의 MIDI 파일)
- 988,983개의 64마디 시퀀스들을 학습에 사용하고 11,295개를 validation에 사용
- 각 시퀀스는 MusicVAE를 사용하여 32개의 연속적인 latent embedding으로 인코딩됨
- MusicVAE의 softmax temperature는 0.001
- Baseline: TransformerMDN (autoregressive transformer)
- Training
- Adam optimizer, batch size 64, 50만 step
- Learning rate는 0.001이고 decay rate 0.98로 매 4000 step마다 decay
- NVIDIA Tesla V100 GPU에서 6.5시간 소요
Framewise Self-similarity Metric
저자들은 모델의 출력과 원래 학습 시퀀스간의 통계적 유사성을 측정하기 위해 로컬한 self-similarity 패턴을 캡처하는 metric을 새로 도입하였다.
2소절의 hop size를 가진 4소절의 sliding window를 사용하여 로컬한 pitch와 duration 통계를 캡처한다. 각 4소절 프레임 내에서 pitch와 duration의 평균과 분산을 계산한다. 이 통계는 각 프레임의 pitch와 duration에 대한 Gaussian PDF를 $(p_P (k), p_D (k))$로 특정한다. 그런 다음 인접한 프레임 $(k, k+1)$의 Overlapping Area (OA)를 pitch($\textrm{OA}_P$)와 duration($\textrm{OA}_D$) 모두에 대하여 다음 식으로 계산한다.
\[\begin{equation} \textrm{OA}(k, k+1) = 1 - \textrm{erf} \bigg( \frac{c - \mu_1}{\sqrt{2} \sigma_1^2} \bigg) + \textrm{erf} \bigg( \frac{c - \mu_2}{\sqrt{2} \sigma_2^2} \bigg) \end{equation}\]여기서 $\mu$와 $\sigma$는 각 프레임의 통계를 $\mathcal{N}(\mu, \sigma)$로 모델링한 것이다. $\textrm{erf}$는 Gauss error function이고 $c$는 $\mu_1 < \mu_2$일 때 Gaussian PDF 사이의 교점이다.
그런 다음 모든 인접한 프레임들 사이의 OA에 대한 평균과 분산인 $\mu_{OA}$와 $\sigma_{OA}^2$를 계산하고, 마찬가지로 위의 방법들을 학습 셋(GT)에 대하여 계산하여 $\mu_{GT}$와 $\sigma_{GT}^2$를 얻는다.
최종적으로 $Consistency$ (C)와 $Variance$ (Var)를 계산할 수 있다.
\[\begin{equation} Consistency = \max (0, 1 - \frac{| \mu_{OA} - \mu_{GT} |}{\mu_{GT}}) \\ Variance = \max (0, 1 - \frac{| \sigma_{OA}^2 - \sigma_{GT}^2 |}{\sigma_{GT}^2}) \end{equation}\]C와 Var이 클수록 모델의 출력과 학습 시퀀스가 통계적으로 유사하다는 것을 의미한다.
Latent Space Evaluation
저자들은 생성된 latent embedding의 유사성을 평가하기 위해 Fréchet distance (FD)와 Maximum Mean Discrepancy (MMD)를 사용하였다. 이 metric들은 모델의 출력과 데이터의 latent space 사이 거리를 평가한다. 이 metric들은 생성된 시퀀스의 장기적인 시간적 일관성이나 품질을 측정하지 않으며 최종 시퀀스가 MusicVAE 디코더로 생성되기 전에 중간의 연속적인 표현의 품질만 측정한다는 점에 유의해야 한다.
Reseult
다음은 C와 Var을 unconditional sampling과 infilling에 대하여 계산한 표이다.
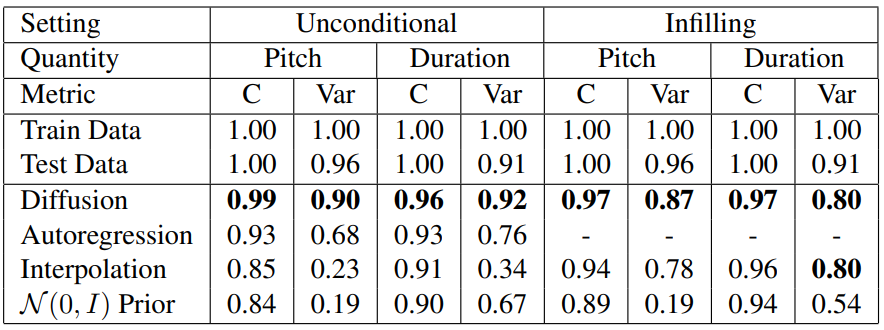
다음은 정규화하지 않은 framewise self-similarity를 계산한 표이다.

Diffusion model은 autoregressive와 달리 모든 latent를 동시에 모델링하는 방법을 학습하기 때문에 시퀀스의 결합 종속성을 더 잘 포착할 수 있다.
다음은 latent space를 평가한 표이다.
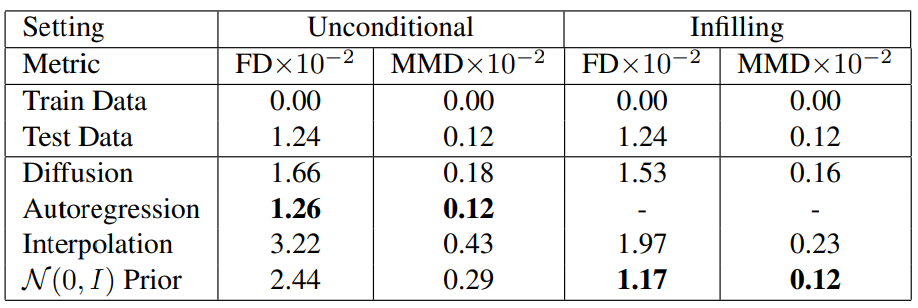
TransformerMDN이 latent space를 더 잘 표현하는 것으로 나타났다. 또한 latent space metric은 latent manifold 분포에 대한 가정에 의해 제한되며 전체 space의 디테일을 완전히 캡처할 수 없으므로 정량적 framewise self-similarity metric과 정성적 평가의 필요성이 더욱 강조된다.
다음은 reverse process가 진행됨에 따라 샘플 품질이 개선되는 것을 보여주는 표이다.
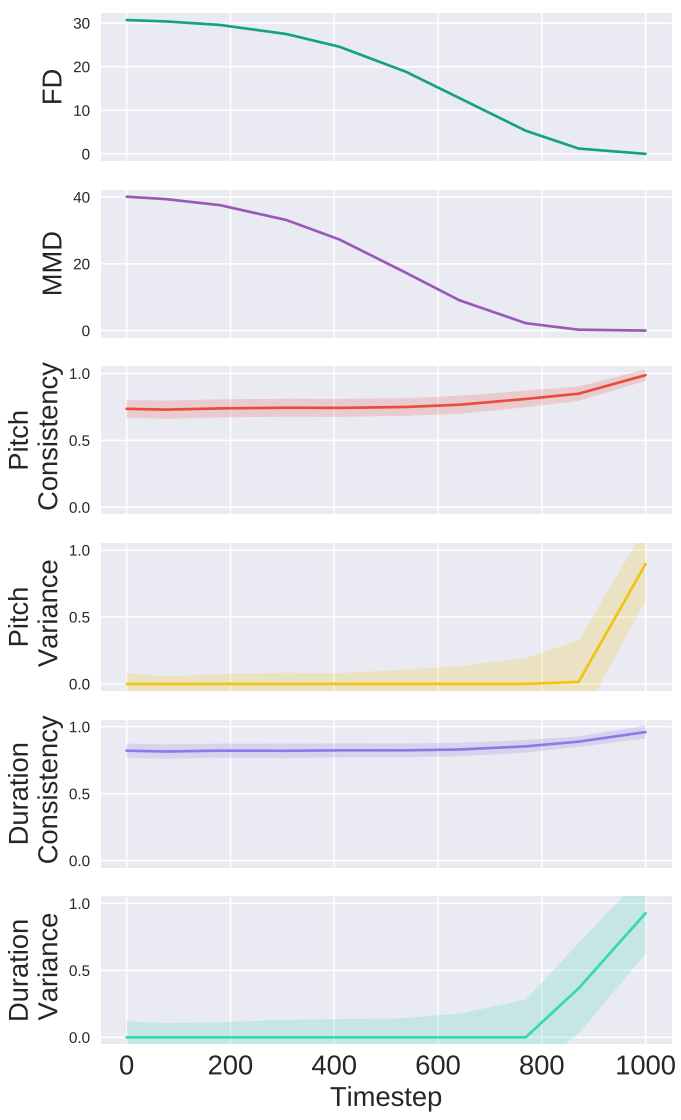
다음은 빨간 박스를 모델이 채우는 infilling 실험의 결과이다.
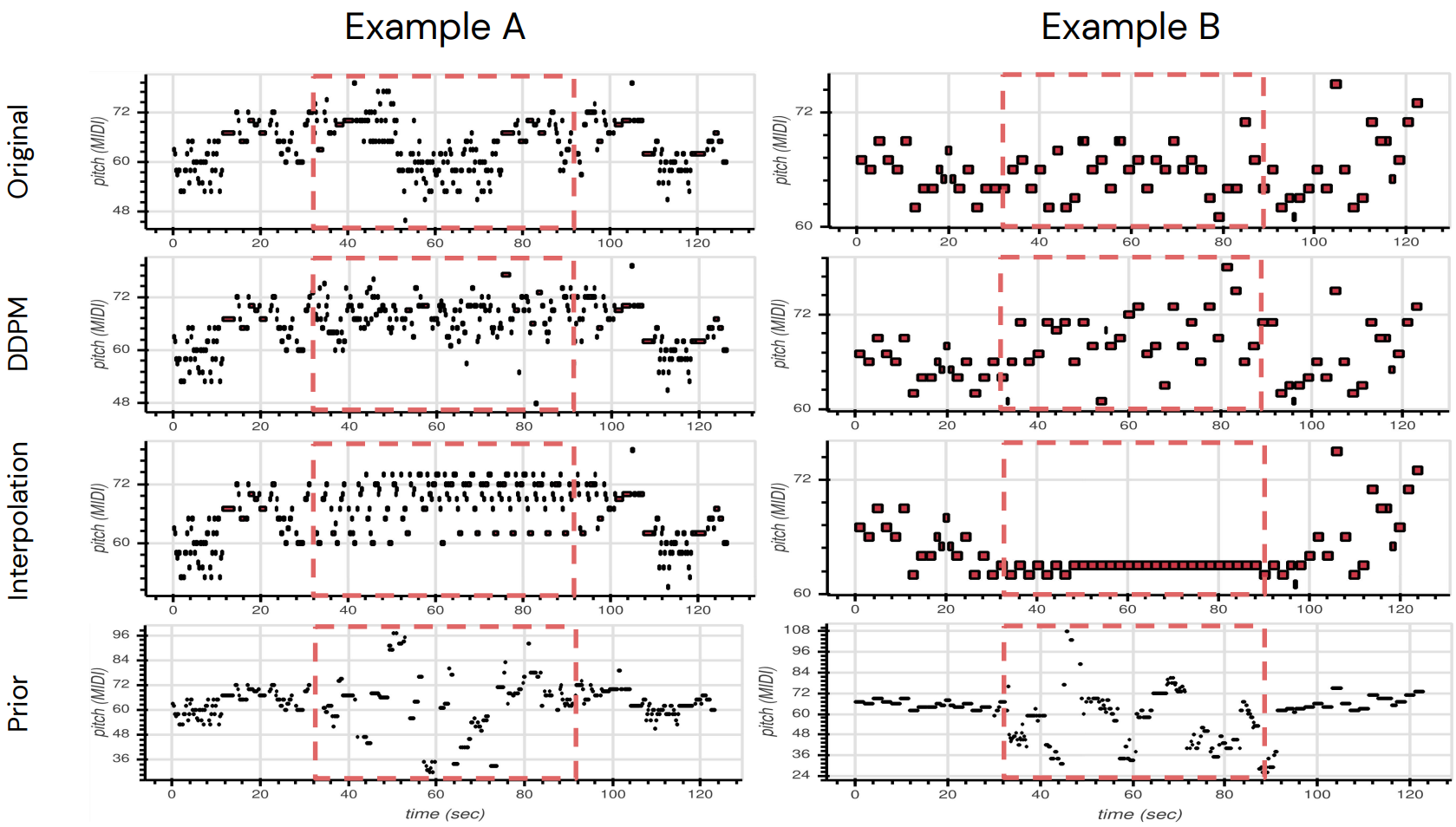
본 논문의 모델이 원본과 가장 비슷하게 infilling을 수행하였다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)