Blogs

ICML 2022. [Paper] [Github] [Page]
Michael Janner, Yilun Du, Joshua B. Tenenbaum, Sergey Levine
University of California, Berkeley | MIT
20 May 2022

Introduction

학습된 모델을 사용한 planning은 강화 학습과 데이터 기반 의사 결정을 위한 개념적으로 간단한 프레임워크이다. 미지의 환경(enviroment) 역학을 근사할 때 지도 학습 문제에 해당하는 부분에만 학습 테크닉을 사용하므로, 가장 효과적인 경우에만 학습 테크닉을 사용한다. 그런 다음, 학습된 모델은 원래 컨텍스트에서 유사하게 잘 이해되는 고전적인 궤적 최적화 루틴에 연결될 수 있다.

그러나 이 조합은 설명대로 거의 작동하지 않는다. 강력한 궤적 최적화 프로그램은 학습된 모델을 활용하기 때문에 이 절차에 의해 생성된 planning은 종종 최적의 궤적보다 적대적인 예처럼 보인다. 결과적으로 현대 model-based 강화 학습 알고리즘은 궤적 최적화 도구보다 value function과 policy gradient와 같은 model-free 방법에서 더 많은 것을 상속받는 경우가 많다. On-line planning에 의존하는 방법은 random shooting과 cross-entropy 방법과 같은 간단한 gradient-free 궤적 최적화 루틴을 사용하는 경향이 있다.

본 논문에서는 데이터 기반 궤적 최적화에 대한 대안적인 접근 방식을 제안한다. 핵심 아이디어는 모델에서 샘플링하고 planning하는 것이 거의 동일해진다는 점에서 궤적 최적화에 직접적으로 순응하는 모델을 학습시키는 것이다. 이 목표를 달성하려면 모델 설계 방식에 변화가 필요하다. 학습된 역학 모델은 일반적으로 환경 역학에 대한 proxy(대리)를 의미하기 때문에 기본 인과 과정에 따라 모델을 구조화하여 개선이 이루어지는 경우가 많다. 대신 사용할 planning 문제에 따라 모델을 설계하는 방법을 고려한다. 예를 들어, 모델은 궁극적으로 planning에 사용되기 때문에 action 분포는 state만큼 중요하며 long-horizon 정확도는 single-step error보다 더 중요하다. 반면에 모델은 학습 중에 여러 task에서 사용될 수 있도록 reward function과 무관하게 유지되어야 한다. 마지막으로 모델은 예측뿐만 아니라 planning이 경험을 통해 개선되고 표준 shooting 기반 planning 알고리즘의 근시적 failure mode에 저항할 수 있도록 설계되어야 한다.

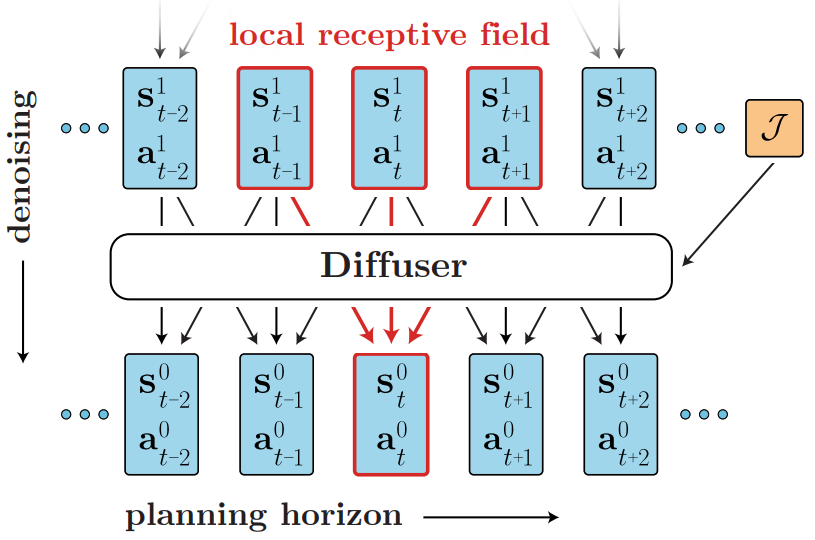
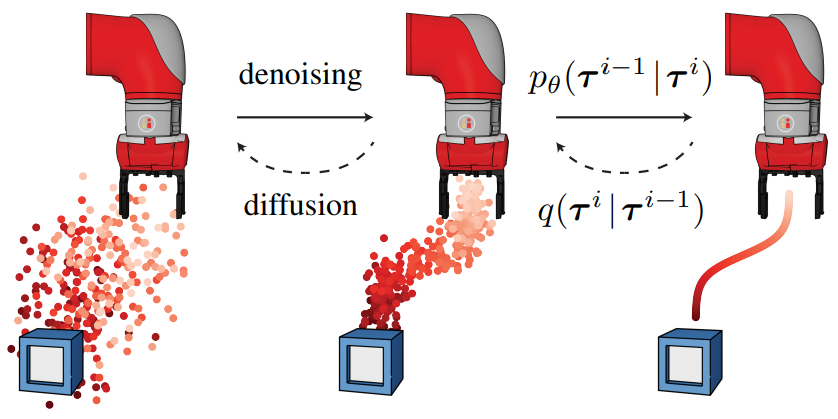
저자들은 이 아이디어를 위 그림에서 시각화된 Diffuser라고 하는 궤적 레벨의 diffusion model로 구체화한다. Diffuser는 계획의 모든 timestep을 동시에 예측한다. Diffusion model의 반복 샘플링 프로세스는 유연한 컨디셔닝으로 이어져 보조 가이드가 샘플링 절차를 수정하여 높은 reward를 얻거나 일련의 제약 조건을 만족하는 궤적으로 복구할 수 있도록 한다. 이 데이터 기반 궤적 최적화 공식에는 몇 가지 매력적인 속성이 있다.

1. Long-horizon scalability: Diffuser는 single-step error가 아닌 생성된 궤적의 정확도에 대해 학습하기 때문에 single-step 모델의 복합 rollout error로 인해 어려움을 겪지 않고 long planning horizon과 관련하여 더 우아하게 확장된다.
2. Task compositionality: Reward function은 planning을 샘플링하는 동안 사용할 보조 기울기를 제공하므로 기울기를 함께 추가하여 여러 reward를 동시에 구성하여 간단한 planning 방법을 사용할 수 있게 한다.
3. Temporal compositionality: Diffuser는 로컬 일관성을 반복적으로 개선하여 전역적으로 일관된 궤적을 생성하며, 이를 통해 in-distribution subsequence을 함께 연결하여 새로운 궤적으로 일반화할 수 있도록 한다.
4. Effective non-greedy planning: 모델과 planner 사이의 경계를 모호하게 함으로써 모델의 예측을 향상시키는 학습 절차는 planning 능력을 향상시키는 효과도 있다. 이 디자인은 기존의 많은 planning 방법에서 어려운 것으로 입증된 long-horizon sparse-reward problem을 해결할 수 있다.

Background

1. Problem Setting

Discrete-time system $s_{t+1} = f(s_t, a_t)$에서 궤적 최적화는 timestep별 reward(또는 cost) $r(s_t, a_t)$에 대한 objective $\mathcal{J}$를 최대화(또는 최소화)하는 action의 sequence $a_{0:T}^\ast$를 찾는 것이다.

\[\begin{equation} a_{0:T}^\ast = \underset{a_{0:T}}{\arg \max} \mathcal{J} (s_0, a_{0:T}) = \underset{a_{0:T}}{\arg \max} \sum_{t=0}^T r(s_t, a_t) \end{equation}\]

$\tau = (s_0, a_0, s_1, a_1, \cdots, s_T, a_T)$로 궤적을 나타내며 $\mathcal{J}(\tau)$는 궤적 $\tau$의 objective 값이다.

2. Diffusion Probabilistic Models

\[\begin{equation} p_\theta (\tau^0) = \int p(\tau^N) \prod_{i=1}^N p_\theta (\tau^{i-1} \vert \tau^i) d \tau^{1:N} \\ p_\theta (\tau^{i-1} \vert \tau^i) = \mathcal{N} (\tau^{i-1} \vert \mu_\theta (\tau^i, i), \Sigma^i) \\ \tau := \tau^0, \quad \tau^N = \mathcal{N}(0, I) \end{equation}\]

Parameter $\theta$는 reverse process의 negative log-likelihood의 variational bound를 최소화하여 최적화된다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} = -\mathbb{E}_\tau [\log p_\theta (\tau^0)] \end{equation}\]

Planning with Diffusion

궤적 최적화 기술을 사용하는 데 있어 주요 장애물은 환경 역학 $f$에 대한 지식이 필요하다는 것이다. 대부분의 학습 기반 방법은 근사 모델을 학습하고 기존의 planning 루틴에 연결하여 이 장애물을 극복하려고 시도한다. 그러나 학습된 모델은 ground-truth 모델을 염두에 두고 설계된 planning 알고리즘 유형에 적합하지 않은 경우가 많기 때문에 적대적 사례를 찾아 학습된 모델을 활용한다.

저자들은 모델링과 planning 사이의 긴밀한 결합을 제안한다. 고전적인 planner의 맥락에서 학습된 모델을 사용하는 대신 가능한 한 많은 planning process를 생성 모델링 프레임워크에 포함하여 planning이 샘플링과 거의 동일해진다. 저자들은 궤적의 diffusion model인 $p_\theta (\tau)$를 사용하여 이를 수행한다. Diffusion model의 반복적인 denoising process는 다음 형식의 분포에서 샘플링을 통해 유연한 컨디셔닝에 적합하다.

\[\begin{equation} \tilde{p}_\theta (\tau) \propto p_\theta (\tau) h(\tau) \end{equation}\]

함수 $h(\tau)$는 observation history와 같은 prior, 원하는 결과, reward와 같은 최적화하려는 함수에 대한 정보를 포함할 수 있다. 이 분포에서 inference를 수행하는 것은 궤적 최적화 문제에 대한 확률론적 유추로 볼 수 있다. 왜냐하면 궤적 최적화 문제가 $p_\theta (\tau)$에 물리적으로 의존하면서 동시에 높은 reward $h(\tau)$에 의존하는 궤적을 찾는 문제이기 때문이다. 환경 역학 정보는 $h(\tau)$와 분리되기 때문에 diffusion model $p_\theta (\tau)$는 동일한 환경의 여러 task에 재사용될 수 있다.

1. A Generative Model for Trajectory Planning

Temporal ordering

궤적 모델에서 샘플링하는 것과 planning하는 것 사이의 경계가 흐려지면 비정상적인 제약 조건이 생긴다. 더 이상 시간 순서대로 state를 autoregressive하게 예측할 수 없다. 목표로 컨디셔닝된 inference $p(s_1 \vert s_0, s_T)$를 생각해보면, 다음 state $s_1$은 이전 state뿐만 아니라 미래 state에도 의존한다. 이 예시는 보다 일반적인 원칙의 예시이다. 역학 예측은 인과적이지만 현재가 과거에 의해 결정된다는 점에서 의사 결정과 제어는 현재의 결정이 미래를 조건으로 한다는 점에서 반인과적일 수 있다. 시간적 autoregressive 순서를 사용할 수 없기 때문에 planning의 모든 timestep을 동시에 예측하도록 Diffuser를 설계한다.

Temporal locality

Autoregressive나 Markovian이 아님에도 불구하고 Diffuser는 편안한 형태의 시간적 지역성을 특징으로 한다. Diffusion model은 단일 temporal convolution으로 구성되며, 주어진 예측의 receptive field는 과거와 미래 모두에서 가까운 timestep으로만 구성된다. 결과적으로 denoising process의 각 step은 궤적의 로컬 일관성을 기반으로만 예측할 수 있다. 그러나 이러한 denoising step을 함께 구성하면 로컬 일관성이 글로벌 일관성을 높일 수 있다.

Trajectory representation

Diffuser는 planning을 위해 디자인된 궤적 모델이다. 즉, 모델에서 파생된 컨트롤러의 효율성이 state 예측의 품질만큼 중요하다. 결과적으로 궤적의 state와 action이 공동으로 예측된다. 예측의 목적을 위해 action은 단순히 state의 추가 차원이다. 특히 Diffuser의 입력 및 출력을 다음과 같은 2차원 배열로 나타낸다.

\[\begin{equation} \tau = \begin{bmatrix} s_0 & s_1 & \cdots & s_T \\ a_0 & a_1 & \cdots & a_T \end{bmatrix} \end{equation}\]

Architecture

Diffuser 아키텍처를 위한 3가지 조건이 있다.

1. 전체 궤적은 autoregressive하지 않게 예측되어야 한다.
2. Denoising process의 각 step은 시간적의 로컬해야 한다.
3. 궤적 표현은 한 차원(planning horizon)을 따라 등가성을 허용해야 하지만 다른 차원(state나 action feature)은 허용하지 않는다.

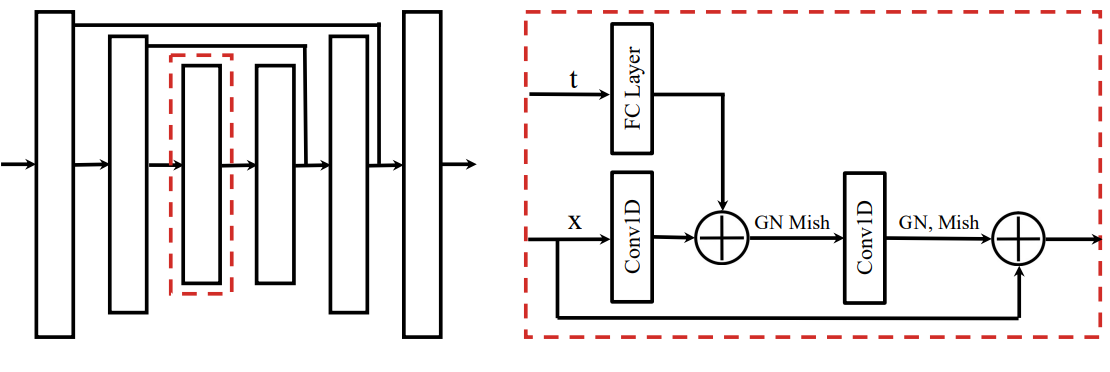
저자들은 반복되는 convolutional residual block으로 구성된 모델로 이러한 기준을 충족한다. 전체 아키텍처는 이미지 기반 diffusion model에서 성공한 U-Net 유형과 유사하지만 2차원 공간 convolution이 1차원 시간 convolution으로 대체되었다. 모델이 완전히 convolution이기 때문에 예측의 horizon은 모델 아키텍처가 아니라 입력 차원에 의해 결정되며, 원하는 경우 planning 중에 동적으로 변경할 수 있다.

Training

저자들은 Diffuser를 사용하여 궤적 denoising process의 학습된 기울기 $\epsilon_\theta (\tau^i, i)$를 parameterize하며, DDPM과 같이 평균 $\mu_\theta$는 closed form으로 구할 수 있다. $\epsilon$-model을 학습하기 위하여 다음과 같은 간단화된 목적 함수를 사용한다.

\[\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{i \sim \mathcal{U}\{1,\cdots,N\}, \epsilon \sim \mathcal{N}(0,i), \tau} [\|\epsilon - \epsilon_\theta (\tau^i, i)\|_2^2] \end{equation}\]

Reverse process의 분산 $\Sigma^i$는 Improved DDPM의 cosine schedule을 사용한다.

2. Reinforcement Learning as Guided Sampling

강화 학습 문제를 Diffuser로 풀기 위하여 reward의 개념을 도입해야 하며, 저자들은 control-as-inference graphical model을 사용한다. $t$에서의 optimality(최적인지 아닌지)를 이진 랜덤 변수 $\mathcal{O}_t$로 나타낸다. 그러면 다음과 같이 최적 궤적 집합 $h(\tau)$에서 샘플링할 수 있다.

\[\begin{equation} \tilde{p}_\theta (\tau) = p(\tau \vert \mathcal{O}_{1:T} = 1) \propto p(\tau) p(\mathcal{O}_{1:T} = 1 \vert \tau) \end{equation}\]

이렇게 두면 강화 학습 문제를 하나의 조건부 샘플링으로 바꿀 수 있다. 다행히도 diffusion model에 대한 조건부 샘플링은 이전 연구들에서 많이 연구되었다. $p(\mathcal{O}_{1:T} \vert \tau^i)$가 충분히 매끄럽다고 하면, reverse diffusion process transition은 가우시안으로 근사할 수 있다.

\[\begin{equation} p_\theta (\tau^{i-1} \vert \tau^i, \mathcal{O}_{1:T}) \approx \mathcal{N} (\tau^{i-1}; \mu + \Sigma g, \Sigma) \\ g = \nabla_{\tau} \log p(\mathcal{O}_{1:T} \vert \tau)|_{\tau = \mu} = \sum_{t=0}^T \nabla_{s_t, a_t} r(s_t, a_t)|_{(s_t, a_t) = \mu_t} = \nabla \mathcal{J} (\mu) \end{equation}\]

이 관계식은 classifier-guided samling 사이의 transition을 제공한다. 먼저 diffusion model $p_\theta (\tau)$을 모든 가능한 궤적의 state와 action에 대하여 학습시킨다. 그런 다음 모델 \(\mathcal{J}_\phi\)가 $\tau^i$의 누적 reward를 예측하도록 학습시킨다. \(\mathcal{J}_\phi\)의 기울기는 reverse process의 $\mu$를 수정하여 궤적 샘플링 과정을 guide하는 데 사용된다. 샘플링된 궤적의 첫번째 action은 환경에서 실행될 수 있으며, 그 후 planning 과정은 표준 receding-horizon control loop에서 다시 시작된다. Guided planning 방법에 대한 pseudocode는 아래 알고리즘과 같다.

3. Goal-Conditioned RL as Inpainting

일부 planning 문제는 reward 극대화보다 제약 조건 만족으로 더 자연스럽게 표현된다. 이러한 세팅에서 objective는 목표 위치에서 종료하는 것과 같은 일련의 제약 조건을 충족하는 실행 가능한 궤적을 생성하는 것이다. 2차원 배열 표현에서 이 세팅은 state와 action 제약 조건이 이미지에서 관찰된 픽셀과 유사하게 작동하는 inpainting 문제로 변환될 수 있다. 배열에서 관찰되지 않은 모든 위치는 관찰된 제약 조건과 일치하는 방식으로 diffusion model에 의해 채워져야 한다.

이 task를 위한 분포는 관찰된 값에 대한 Dirac delta이고 다른 곳에서는 상수이다. 구체적으로, $c_t$가 timestep $t$에서의 state 제약이면, 다음과 같다.

\[\begin{equation} h(\tau) = \delta_{c_t} (s_0, a_0, \cdots, s_T, a_T) = \begin{cases} \infty & \textrm{if } c_t = s_t \\ 0 & \textrm{otherwise} \end{cases} \end{equation}\]

Action 제약에 대한 정의도 동일하다. 실제로 이는 모든 timestep에서 reverse process로 샘플링한 다음 샘플링된 값을 $c_t$로 교체하는 방법으로 구현된다.

모든 샘플링된 궤적은 현재 state에서 시작해야 하기 때문에 reward 최대화 문제도 inpainting으로 컨디셔닝하는 것이 필요하다. (Algorithm 1의 line 10)

Properties of Diffusion Planners

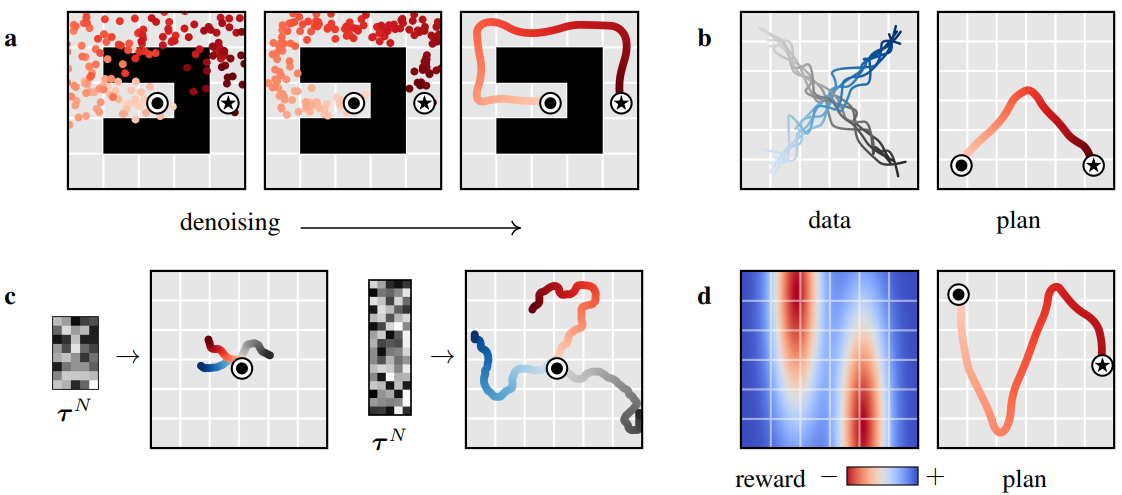
(a) Learned long-horizon planning

Single-step model은 일반적으로 실제 환경 역학 $f$에 대한 proxy로 사용되며, 따라서 특별히 planning 알고리즘에 연결되지 않는다. 반면 Algorithm 1의 planning 루틴은 diffusion model의 특정 affordance와 밀접하게 연결되어 있다. 본 논문의 planning 방법은 샘플링과 거의 동일하기 때문에 (유일한 차이점은 $h(\tau)$에 의한 guidance) long-horizon predictor로서의 Diffuser의 효율성은 효과적인 long-horizon planning으로 직접 변환된다. 우리는 위 그림 (a)의 goal-reaching 세팅에서 학습된 planning의 이점을 보여준다. Diffuser는 shooting 기반 접근 방식이 어려움을 겪는 sparse reward setting에서 실행 가능한 궤적을 생성할 수 있다.

(b) Temporal compositionality

Single-step model은 종종 Markov 속성을 사용하여 in-distribution 전환을 구성하여 out-of-distribution 궤적으로 일반화할 수 있다. Diffuser는 로컬 일관성을 반복적으로 개선하여 전체적으로 일관된 궤적을 생성하기 때문에 익숙한 subsequence를 새로운 방식으로 결합할 수도 있다. 위 그림 (b)에서 직선으로만 이동하는 궤적에 대해 Diffuser를 학습시키고 교차점에서 궤적을 결합하여 v자형 궤적으로 일반화할 수 있음을 보여준다.

(c) Variable-length plans

본 논문의 모델은 horizon 차원에서 완전한 convolution이기 때문에 planning horizon은 아키텍처 선택에 의해 지정되지 않는다. 대신 denoising process를 초기화하는 입력 noise $\tau^N \sim \mathcal{N}(0, I)$의 크기에 의해 결정되므로 가변 길이의 planning이 가능하다.

(d) Task compositionality

Diffuser는 환경에 대한 정보를 모두 포함하고 있지만 reward function과는 독립적이다. 모델은 가능한 미래에 대한 prior로 작용하기 때문에 서로 다른 reward에 해당하는 상대적으로 가벼운 $h(\tau)$에 따라 planning을 guide할 수 있다. 저자들은 위 그림 (d)에서 diffusion model이 학습 중에 못 본 새로운 reward function에 대하여 planning하여 이를 입증하였다.

Experimental Evaluation

1. Long Horizon Multi-Task Planning

저자들은 reward가 1인 목표 위치로 이동해야 하는 Maze2D 환경에서의 long-horizon planning을 평가한다. 다른 위치에서는 reward가 제공되지 않는다. 목표 위치에 도달하는 데 수백 step이 걸릴 수 있기 때문에 최고의 model-free 알고리즘조차도 크레딧 할당을 적절하게 수행하고 안정적으로 목표에 도달하는 데 어려움을 겪는다.

Inpainting 전략을 사용하여 시작과 목표 위치를 조건으로 하는 Diffuser로 planning한다. 그런 다음 샘플링된 궤적을 open-loop plan으로 사용한다. Diffuser는 모든 미로 크기에서 100점 이상의 점수를 얻었으며 이는 reference expert policy를 능가한다. 위 그림은 Diffuser의 plan을 생성하는 reverse diffusion process를 시각화한다.

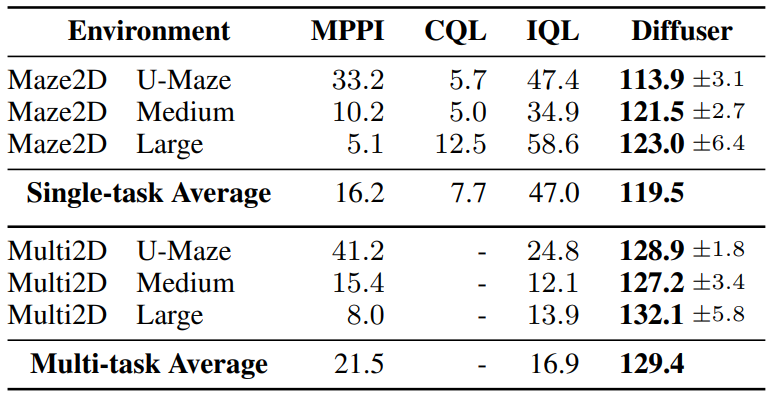
Maze2D의 학습 데이터는 랜덤하게 선택한 위치를 탐색하는 컨트롤러로 구성되어 방향이 지정되지 않지만, 평가는 목표가 항상 동일하다는 점에서 single-task다. Multi-task 유연성을 테스트하기 위해 각 에피소드 시작 시 목표 위치를 랜덤하게 지정하도록 환경을 수정하며, 이 설정은 위 표에서 Multi2D로 표시된다.

Diffuser는 기본적으로 multi-task planner이다. Single-task 실험에서는 모델을 재학습시킬 필요가 없으며 단순히 컨디셔닝 목표를 변경할 필요가 없다. 결과적으로 Diffuser는 single-task에서와 마찬가지로 multi-task에서도 잘 작동한다. 반면 single-task에서의 최고의 model-free 알고리즘은 multi-task에 적응할 때 상당한 성능 저하가 발생한다.

2. Test-time Flexibility

새로운 test-time 목표로 일반화하는 능력을 평가하기 위해 세 가지 설정으로 블록 쌓기 task를 구성한다.

1. Unconditional Stacking: 최대한 블럭을 높게 쌓는 task
2. Conditional Stacking: 정해진 순서대로 블럭을 쌓는 task
3. Rearrangement: 블럭의 위치를 새로운 배열로 일치시키는 task

저자들은 PDDLStream에서 생성된 데모에서 10000개의 궤적에 대한 모든 방법을 학습시킨다. Reward는 성공적으로 배치하면 1이고 그렇지 않으면 0이다. 이러한 블록 쌓기는 test-time 유연성에 대한 어려운 진단이며, 랜덤 목표를 위해 부분적인 쌓기를 실행하는 과정에서 컨트롤러는 학습에 포함되지 않은 새로운 state로 모험을 떠난다.

저자들은 모든 블록 쌓기 task에 하나의 학습된 Diffuser를 사용하고 함수 $h(\tau)$만 수정하였다. Unconditional Stacking task에서는 PDDLStream 컨트롤러를 실행하기 위해 denoising process $p_\theta(\tau)$에서 직접 샘플링한다. Conditional Stacking과 Rearrangement task에서는 샘플링된 궤적을 편향시키기 위해 두 가지 $h(\tau)$를 구성한다. 첫 번째는 궤적의 최종 state가 목표와 일치할 likelihood를 최대화하고 두 번째는 동작 중에 end effector와 큐브 사이에 접촉 제약 조건을 적용한다.

저자들은 두 가지 model-free offline 강화학습 알고리즘 BCQ, CQL와 본 논문의 모델을 비교하였다. 비교에 대한 정량적 결과는 아래 표와 같다. (100점 만점)

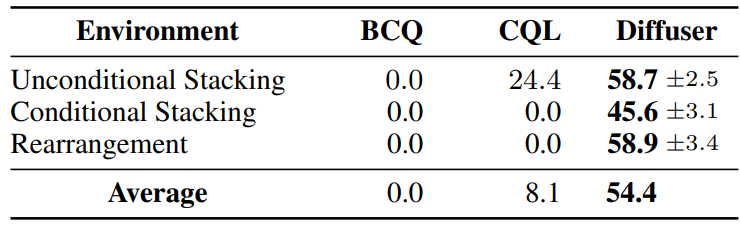
Diffuser의 실행 결과의 시각적 묘사는 아래 그림과 같다.

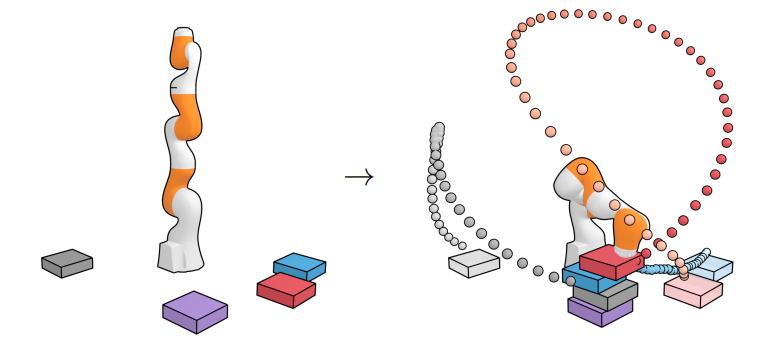
3. Offline Reinforcement Learning

마지막으로 저자들은 D4RL offline locomotion suite를 사용하여 다양한 품질의 데이터에서 효과적인 single-task 컨트롤러를 복구하는 능력을 평가한다. 다양한 데이터 기반 제어 알고리즘과 비교한 결과는 아래와 같다.

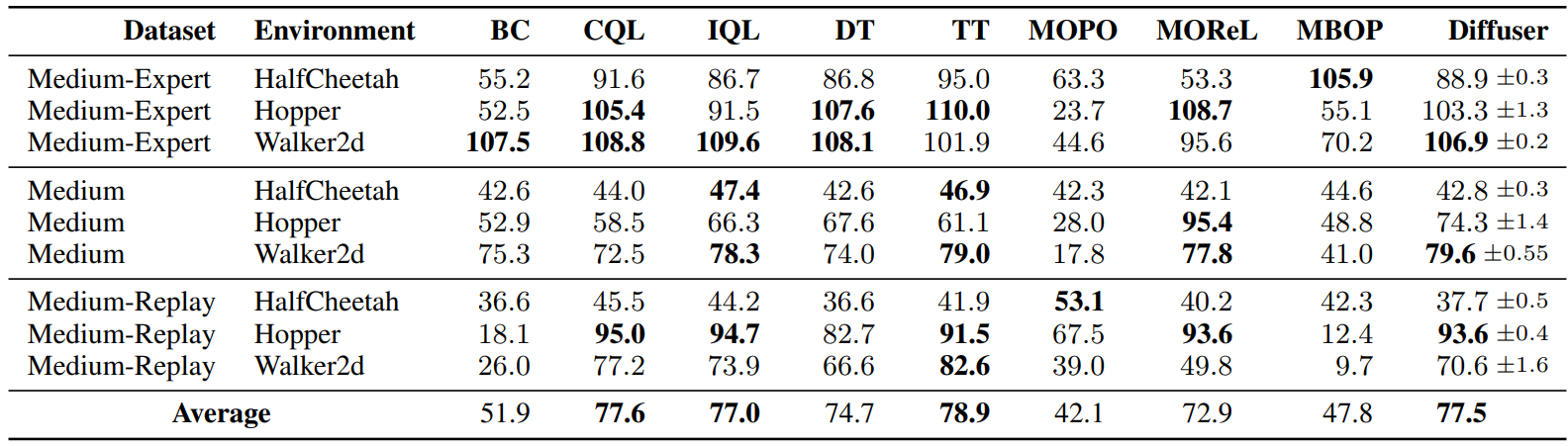
4. Warm-Starting Diffusion for Faster Planning

Diffuser의 한계점은 개별 planning의 생성 속도가 느리다는 것이다. Open loop를 실행할 때 실행의 각 step에서 새로운 planning을 재생성해야 한다. Diffuser의 실행 속도를 개선하기 위해 이전에 생성된 plan을 추가로 재사용하여 후속 plan의 생성을 warm-start할 수 있다. Warm-start planning을 위해 이전에 생성된 plan에서 제한된 수의 forward diffusion step을 실행한 다음 이 궤적에서 해당하는 denoising step을 실행하여 업데이트된 plan을 재생성할 수 있다.

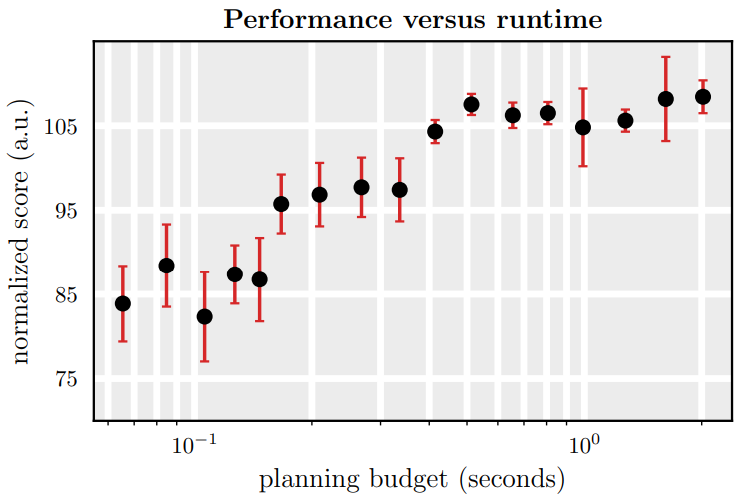
위 그림은 각각의 새 plan을 재생성하는 데 사용되는 denoising step의 기본 수를 2에서 100으로 변경함에 따라 성능과 런타임 사이의 균형을 보여준다.

5. Guided sampling

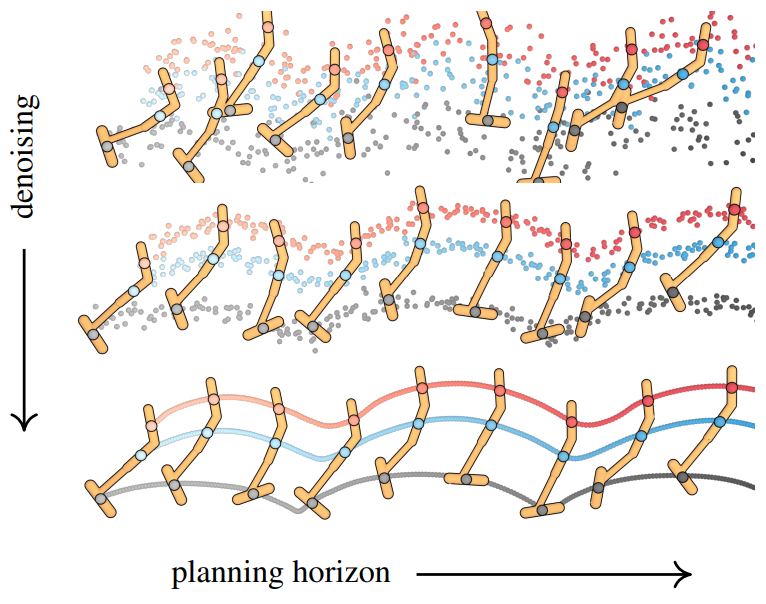
아래 그림은 Diffuser가 autoregressive하지 않으며 denoising process를 통해 모든 timestep를 생성함을 보여준다.