ICLR 2021. [Paper] [Page]
Alex Nichol, Prafulla Dhariwal
OpenAI
18 Feb 2021
Introduction
Deep unsupervised learning using nonequilibrium thermodynamics 논문은 점진적인 여러 step의 noising process를 reverse하는 것을 학습하여 데이터 분포를 매칭하는 생성 모델의 클래스인 diffusion probabilistic model을 도입하였다. 최근에 DDPM 논문은 DDPM과 score 기반 생성 모델의 등가성을 보였다. Diffusion model은 고품질 이미지를 생성할 수 있음을 보였지만 autoregressive model과 같은 likelihood 기반 모델의 log-likelihood를 달성하지 못하였다. 이는 DDPM이 분포의 모든 모드를 캡처할 수 있는 지에 대한 질문을 하게 한다. 또한 DDPM이 CIFAR-10과 LSUN 데이터셋에서 굉장히 좋은 결과를 보였지만 ImageNet과 같은 다양성이 높은 데이터셋에 적용할 수 있는지 불분명하다.
본 논문에서는 DDPM이 ImageNet과 같은 다양성이 높은 데이터셋에서도 likelihood 기반 모델의 log-likelihood를 달성할 수 있음을 보인다. Variational lower bound (VLB)를 더 잘 최적화하기 위하여 간단한 reparameterization과 VLB와 DDPM의 간단한 목적 함수를 합친 하이브리드 목적 함수를 사용하여 reverse process의 분산을 학습시킨다.
저자들은 하이브리드 목적 함수를 사용하면 바로 log-likelihood를 최적화하는 것보다 더 좋은 log-likelihood를 얻을 수 있다고 하며, 바로 log-likelihood를 최적화하는 목적 함수가 더 많은 기울기 noise를 학습 중에 가진다고 한다. 본 논문에서는 이 noise를 줄이는 간단한 중요도 샘플링 테크닉을 보여주며, 더 좋은 log-likelihood를 얻을 수 있다고 한다.
학습된 분산을 모델에 통합하면 아주 작은 샘플 품질의 변화를 보이면서 더 적은 step으로 샘플링할 수 있다고 한다. DDPM이 수백 번의 pass로 좋은 샘플을 생성할 때, 본 논문의 모델은 50번의 pass만으로 좋은 샘플을 생성한다고 하며, 이를 DDIM과 비교한다.
Improving the Log-likelihood
DDPM은 FID와 Inception Score 측면에서 높은 fidelity의 샘플을 생성할 수 있음을 발견했지만 이러한 모델로는 경쟁력 있는 log-likelihood를 달성할 수 없었다. Log-likelihood는 생성 모델링에서 널리 사용되는 메트릭이며 일반적으로 log-likelihood을 최적화하면 생성 모델이 데이터 분포의 모든 모드를 캡처하도록 강제하는 것으로 여겨진다. 또한 최근 연구에서는 log-likelihood의 작은 개선이 샘플 품질 및 학습된 feature 표현에 큰 영향을 미칠 수 있음을 보여주었다. 따라서 DDPM이 이 메트릭에서 제대로 수행되지 않는 것처럼 보이는 이유를 조사하는 것이 중요하며, 이는 잘못된 mode coverage와 같은 근본적인 단점을 암시할 수 있기 때문이다. 이 섹션에서는 DDPM 알고리즘에 대한 몇 가지 수정 사항을 살펴본다. 수정 사항을 적용할 시 DDPM은 이미지 데이터셋에서 훨씬 더 나은 log-likelihood를 달성할 수 있으며 다른 likelihood 기반 생성 모델과 동일한 이점을 누릴 수 있다.
다양한 수정의 효과를 연구하기 위해 ImageNet 64$\times$64와 CIFAR-10 데이터셋에서 고정된 hyperparameter로 고정된 모델 아키텍처를 학습시킨다. 저자들은 ImageNet 64$\times$64이 다양성과 해상도 사이에 좋은 trade-off를 제공하여 overfitting에 대한 걱정 없이 모델을 빠르게 학습시킬 수 있기 때문에 ImageNet 64$\times$64도 연구하기로 하였다고 한다. 또한 ImageNet 64$\times$64는 생성 모델링의 맥락에서 광범위하게 연구되어 다른 생성 모델과 직접 비교할 수 있다. DDPM의 setup을 사용한 경우 ImageNet 64$\times$64에서 3.99 bits/dim의 log-likelihood를 달성하였다고 한다.
1. Learning $\Sigma_\theta (x_t, t)$
DDPM에서는 $\Sigma_\theta (x_t, t) = \sigma_t^2 I$로 설정하였으며, $\sigma_t$는 학습하지 않는다. $\sigma_t^2$을 $\beta_t$로 두나 $\tilde{\beta}_t$로 두나 같은 샘플 품질을 얻었다고 한다.
$\beta_t$와 $\tilde{\beta}_t$가 두 반대 극단을 나타내는 것을 고려하면, 어떤 것을 선택하던지 샘플에 영향을 미치지 않는지 궁금증이 생긴다. 이에 대한 하나의 단서는 아래 그래프에서 볼 수 있다.
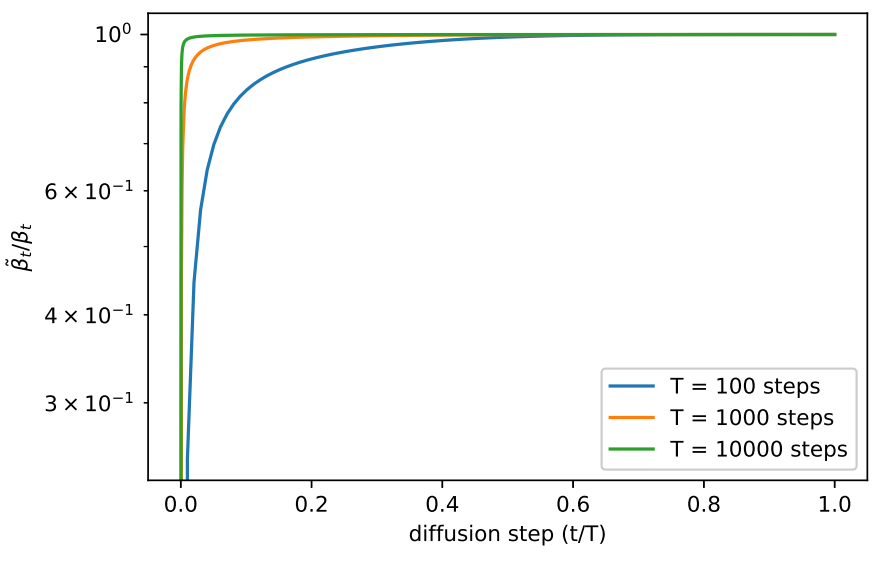
$\beta_t$와 $\tilde{\beta}t$는 눈에 띄지 않는 디테일을 다루는 $t = 0$ 근처를 제외하면 거의 같다. 또한 diffusion step의 수를 증가시키면 더 많은 diffusion process가 가까워진다. 이는 무한한 diffusion step에서 $\sigma_t$의 선택이 샘플 품질에 전혀 영향을 주지 않으며, 모델 평균 $\mu\theta (x_t, t)$가 $\Sigma_t (x_t, t)$보다 더 많이 분포를 결정한다는 것을 의미한다.
$\sigma_t$를 고정하는 것이 샘플 품질에는 합리적인 선택이지만, log-likelihood에 대해서는 그렇지 않다.
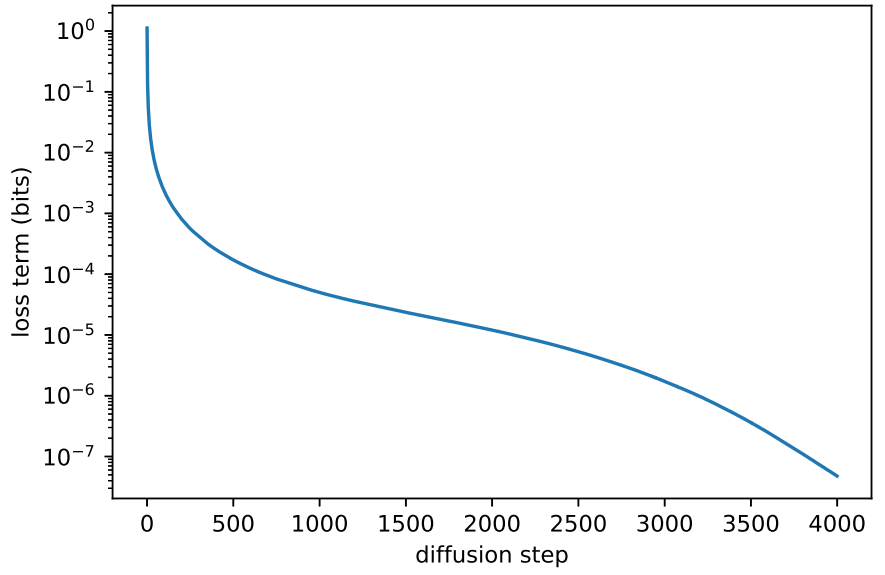
위 그림은 diffusion process의 초기 몇 step이 대부분의 VLB에 기여한다는 것을 보여준다. 따라서, $\Sigma_\theta (x_t, t)$를 더 잘 선택한다면 log-likelihood를 개선할 수 있다. 이를 달성하기 위해 $\Sigma_\theta (x_t, t)$의 불안정하지 않은 학습이 필요하다.
$\Sigma_\theta (x_t, t)$에 대한 합리적인 범위가 매우 좁기 때문에 신경망이 $\Sigma_\theta (x_t, t)$를 바로 예측하는 것이 어려울 수 있다. 그 대신에 로그 도메인에서 분산을 $\beta_t$와 $\tilde{\beta}_t$의 보간으로 parameterize하는 것이 좋다. 본 논문의 모델은 벡터 $v$를 출력하며, $v$로 분산을 다음과 같이 정의한다.
\[\begin{equation} \Sigma_\theta (x_t, t) = \exp(v \log \beta_t + (1-v) \log \tilde{\beta}_t) \end{equation}\]저자들은 $v$에 대한 어떠한 제약도 두지 않았으므로 이론적으로는 보간 범위 밖의 값을 예측할 수도 있다. 하지만 실제로는 보간 범위 안의 값을 예측하며, 이는 $\Sigma_\theta (x_t, t)$에 대한 경계가 실제로 충분히 표현할 수 있음을 시사한다.
$L_\textrm{simple}$이 $\Sigma_\theta (x_t, t)$에 의존하지 않으므로 저자들은 새로운 하이브리드 목적 함수를 정의하였다.
\[\begin{equation} L_\textrm{hybrid} = L_\textrm{simple} + \lambda L_\textrm{vlb} \end{equation}\]실험에서는 $\lambda = 0.001$로 두어 $L_\textrm{vlb}$가 $L_\textrm{simple}$을 압도하지 않도록 하였으며, 같은 이유로 $L_\textrm{vlb}$ 항에 대해서는 $\mu_\theta (x_t, t)$ 출력에 stop-gradient를 적용하였다고 한다. 이런 방법을 통해 $\mu_\theta (x_t, t)$가 여전히 가장 큰 영향을 끼치면서 $L_\textrm{vlb}$가 $\Sigma_\theta (x_t, t)$를 guide하도록 한다.
2. Improving the Noise Schedule
저자들은 DDPM에서 사용한 linear noise schedule이 고해상도 이미지에서 잘 작동하지만 64$\times$64나 32$\times$32에서는 차선책이라고 말한다. 특히, forward noise process의 끝이 너무 noisy하여 샘플 품질에 많은 기여를 못한다고 한다. 이는 아래 그림에서 확인할 수 있다.

이 결과에 대한 효과는 아래 그래프와 같다. 아래 그래프는 ImageNet 64$\times$64에서 reverse diffusion의 앞부분을 생략하였을 때의 FID를 측정한 것이다.

Linear schedule로 학습한 모델은 reverse process의 앞 부분 20%를 생략해도 FID가 그렇게 나빠지지 않는다.
이 문제를 해결하기 위해 저자들은 새로운 diffusion nosie schedule을 $\bar{\alpha}_t$의 항으로 구성한다.
\[\begin{equation} \bar{\alpha}_t = \frac{f(t)}{f(0)}, \quad f(t) = \cos \bigg( \frac{t/T + s}{1 + s} \cdot \frac{\pi}{2} \bigg)^2 \\ \beta_t = 1 - \frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}} \end{equation}\]실제로는 $t = T$ 근처의 diffusion process 끝 부분에서의 특이점을 방지하기 위해 $\beta_t$가 0.999를 넘지 못하도록 clip한다.
이 cosine schedule은 process 중간에서 $\bar{\alpha}_t$의 선형적인 감소를 보이면서, 양 극단 $t = 0$과 $t = T$에서는 급격한 변화가 생기지 않도록 디자인되었다.
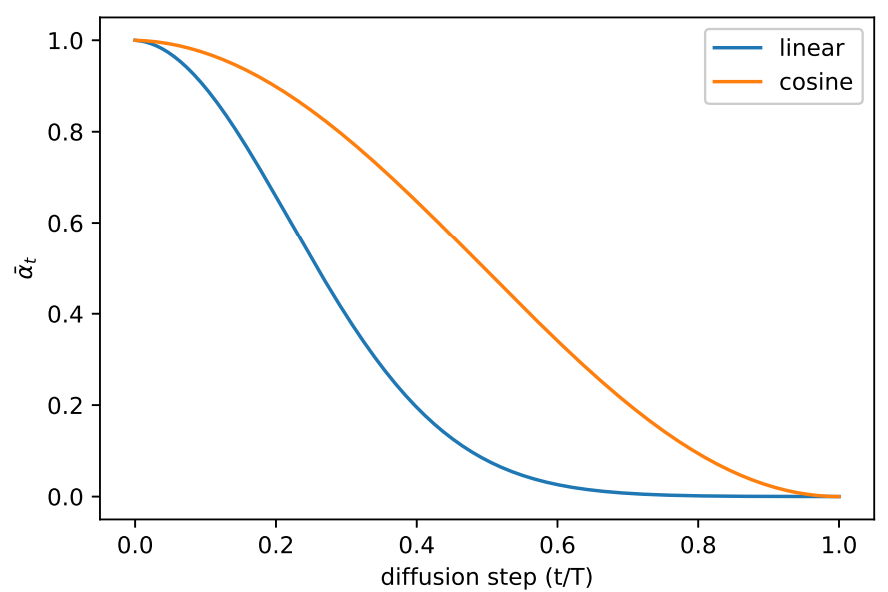
위 그래프는 cosine schedule과 linear schedule을 비교하여 보여준다. DDPM의 linear schedule은 0으로 빠르게 떨어지기 때문에 정보의 파괴가 필요한 정도보다 더 빠르다.
저자들은 process 초기의 작은 noise는 신경망이 $\epsilon$을 정확하게 예측하기 어렵게 만들기 때문에, 작은 offset $s$를 사용하여 $beta_t$가 $t = 0$ 근처에서 너무 작아지지 않게 한다. 특히, $\sqrt{\beta_0}$이 pixel bin size $1/127.5$보다 조금 작도록 $s = 0.008$로 둔다. 코사인의 제곱을 사용한 것은 원하는 디자인에 맞는 간단한 함수이기 때문이며, 비슷한 모양의 다른 함수도 잘 작동할 것이다.
3. Reducing Gradient Noise
저자들은 $L_\textrm{hybrif}$를 최적화하는 대신 $L_\textrm{vlb}$를 바로 최적화하여 최고의 log-likelihood를 달성하고자 하였다. 하지만 실제로 ImageNet 64$\times$64에서 $L_\textrm{vlb}$를 최적화하는 것이 어려웠다고 한다.
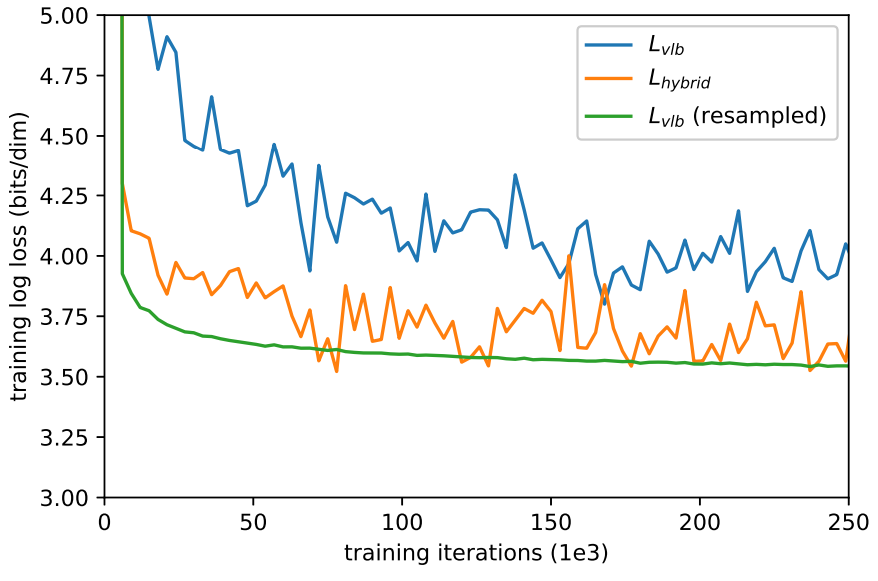
위 그래프는 $L_\textrm{vlb}$와 $L_\textrm{hybrid}$의 학습 곡선을 보여준다. 두 곡선이 모두 noisy하지만 하이브리드 목적 함수가 같은 학습 시간동안 더 좋은 log-likelihood를 달성한다는 것을 알 수 있다.
저자들은 $L_\textrm{vlb}$가 $L_\textrm{hybrid}$에 비해 더 noisy하다고 가정하였다. 이를 확인하기 위하여 각 목적 함수로 학습한 모델의 gradient noise scale을 평가하였으며, 그 결과는 아래 그래프와 같다.

따라서 log-likelihood를 직접 최적화하기 위해 $L_\textrm{vlb}$의 분산을 줄이는 방법을 찾았다. $L_\textrm{vlb}$가 $t$에 따라 굉장히 다른 크기를 갖기 때문에 $t$를 균등하게 샘플링하는 것이 불필요하다. 이를 해결하기 위해 다음과 같은 중요도 샘플링을 수행한다.
$\mathbb{E}[L_t^2]$를 알 수 없고 학습 중에 바뀔 수 있기 때문에 이전 10개의 값을 저장해두었다가 사용하며 학습 중에 동적으로 업데이트한다. 학습 초기에는 모든 $t \in [0, T-1]$의 샘플이 10개씩 모이기 전까지 $t$를 균등하게 샘플링한다.
이러한 중요도 샘플링된 목적 함수를 사용하면 최고의 log-likelihood를 얻을 수 있다. 앞의 학습 곡선 그래프에서 $L_\textrm{vlb}$ (resampled) 곡선을 확인할 수 있으며, 중요도 샘플링된 목적 함수가 원래의 균등하게 샘플링된 목적 함수보다 덜 noisy함을 알 수 있다. 또한 덜 noisy한 $L_\textrm{hybrid}$를 직접 최적화하는 데는 중요도 샘플링 테크닉이 효과적이 않다고 한다.
4. Results and Ablations
다음 표는 ImageNet 64$\times$64에서의 더 나은 log-likelihood를 얻기 위한 ablation study 결과이다.

다음 표는 CIFAR-10에서의 더 나은 log-likelihood를 얻기 위한 ablation study 결과이다.

$L_\textrm{hybrid}$와 cosine schedule을 사용하면 FID를 DDPM만큼 유지하면서 log-likelihood를 개선한다. $L_\textrm{vlb}$를 사용하면 log-likelihood를 개선할 수 있지만 FID가 높아지므로 $L_\textrm{hybrid}$를 사용하는 것이 더 좋다.
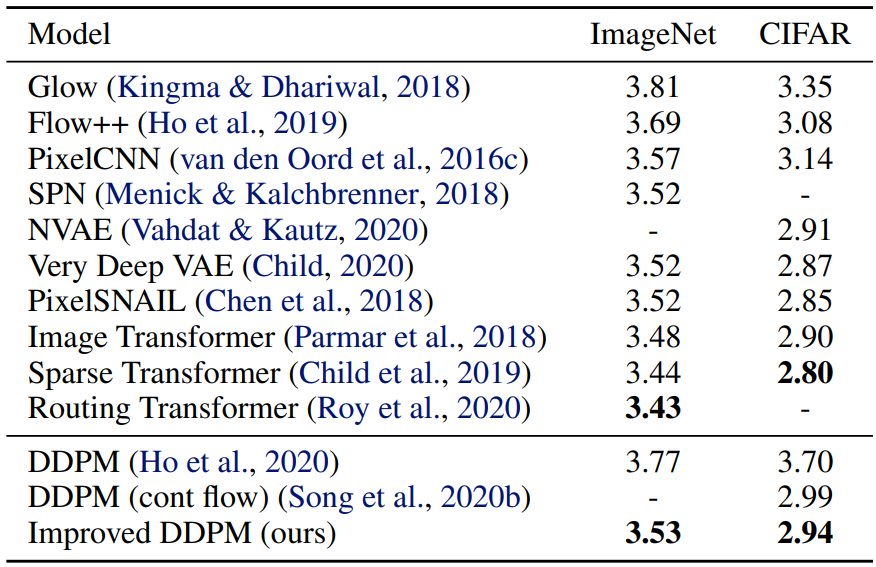
다음 표는 이전 논문의 모델과 본 논문의 가장 좋은 모델의 NLL(negative log-likelihood, bits/dim)를 비교한 표이다.
Improving Sampling Speed
본 논문의 모든 모델은 4000 diffusion step으로 학습되었으므로 하나의 샘플을 생성하는 데 최근 GPU로 몇 분이 소요된다. 저자들은 어떻게 하면 사전 학습된 $L_\textrm{hybrid}$ 모델로 고품질 샘플을 생성하면서 diffusion step을 줄일 수 있는 지 연구하였다.
$T$ diffusion step으로 학습된 모델에 대하여 일반적으로 학습과 동일하게 $t$ 값들의 수열 $(1, 2, \cdots, T)$로 샘플링한다. 반면, $t$ 값들의 임의의 부분 수열 $S$를 사용하여 샘플링하는 것도 가능하다. 학습 noise schedule $\bar{\alpha}_t$가 주어지면 다음과 같이 $S$에 대한 샘플링 noise schedule \(\bar{\alpha}_{S_t}\)를 얻을 수 있다.
\[\begin{equation} \beta_{S_t} = 1 - \frac{\bar{\alpha}_{S_t}}{\bar{\alpha}_{S_{t-1}}}, \quad \tilde{\beta}_{S_t} = \frac{1 - \bar{\alpha}_{S_{t-1}}}{1 - \bar{\alpha}_{S_t}} \beta_{S_t} \end{equation}\]$\Sigma_\theta (x_{S_t} , S_t)$가 $\beta_{S_t}$와 \(\tilde{\beta}_{S_t}\) 사이로 parameterize되기 때문에 자동으로 더 rescale된다. 따라서
\[\begin{equation} p(x_{S_{t-1}} \vert x_{S_t}) = \mathcal{N} (\mu_\theta (x_{S_t}, S_t), \Sigma_\theta (x_{S_t}, S_t)) \end{equation}\]로 계산할 수 있다. 샘플링 step의 수를 $T$에서 $K$로 줄이기 위해서 1과 $T$ 사이의 균등 간격 실수 $K$를 사용한 다음 각 결과 숫자를 가장 가까운 정수로 반올림한다.
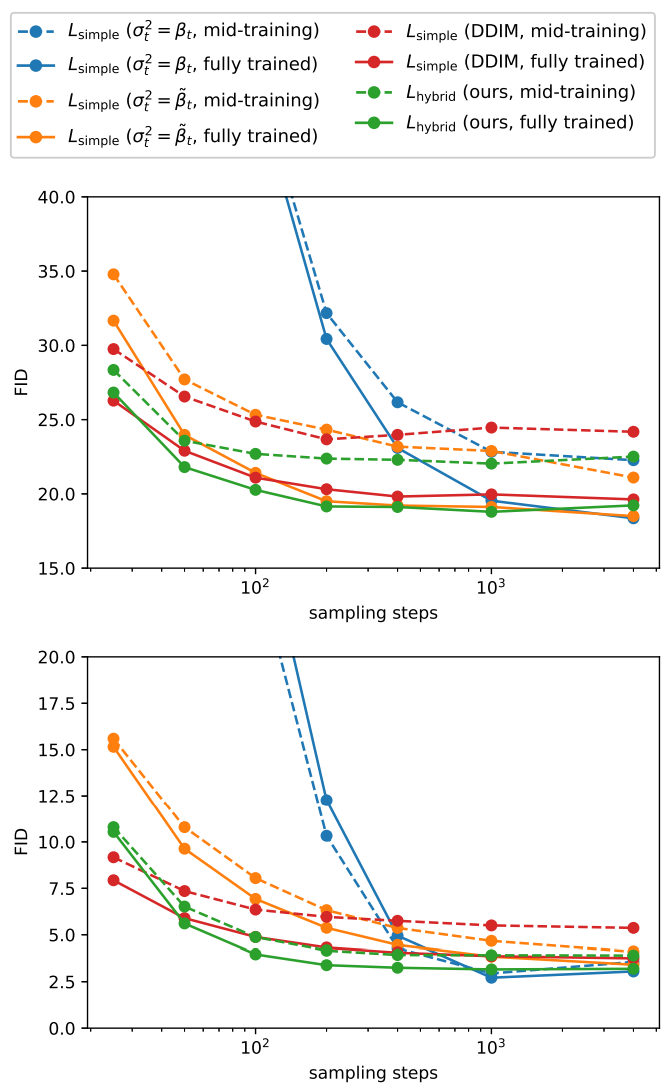
위 그림에서는 25, 50, 100, 200, 400, 1000, 4000 샘플링 step을 사용하여 4000 diffusion step으로 학습된 $L_\textrm{hybrid}$ 모델과 $L_\textrm{simple}$ 모델에 대한 FID를 평가한다. 위의 그래프가 ImageNet 64$\times$64에 대한 FID이고 아래가 CIFAR-10에 대한 FID이다.
고정된 분산을 사용하는 $L_\textrm{simple}$ 모델은 샘플링 단계 수를 줄일 때 샘플 품질이 훨씬 더 나빠지는 반면 학습된 분산을 사용하는 $L_\textrm{hybrid}$ 모델은 높은 샘플 품질을 유지한다. 이 모델을 사용하면 100개의 샘플링 step으로 완전히 학습된 모델에 대한 최적에 가까운 FID를 달성하기에 충분하다. 또한, DDIM을 사용하는 경우 50보다 적은 수의 샘플링 step을 사용할 때는 더 나은 샘플을 생성하였지만, 그보다 많은 step에서는 더 품질이 낮은 샘플을 생성한다.
Comparison to GANs
다음은 ImageNet 64$\times$64에서 클래스 조건부 생성에 대한 샘플 품질을 비교한 표이다.

다음은 FID 2.92를 기록한 모델에서 250개의 샘플링 step으로 ImageNet 64$\times$64 샘플을 생성한 것이다.

각 클래스에 대한 높은 다양성을 보여주었으며 타겟 분포에 대한 좋은 coverage를 보였다.
Scaling Model Size
다음은 다양한 모델 크기에 대한 FID와 NLL 결과를 나타낸 것이다.
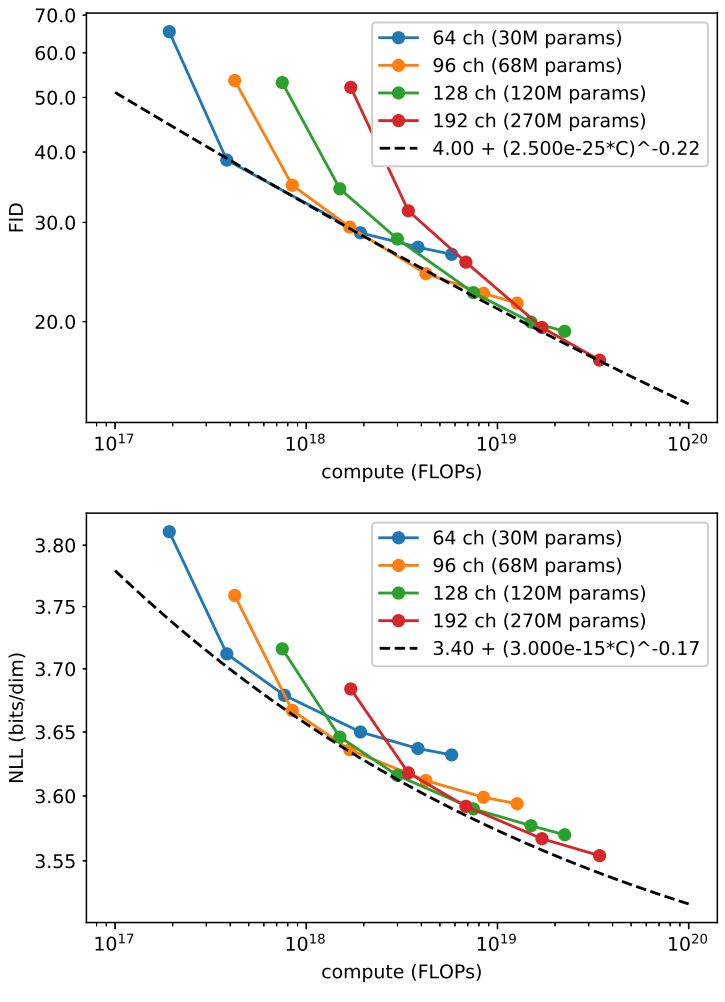
학습량이 많을수록 FID와 NLL이 개선되는 것을 볼 수 있다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)