arXiv 2023. [Paper] [Page]
Sihyun Yu, Kihyuk Sohn, Subin Kim, Jinwoo Shin
KAIST | Google Research
15 Feb 2023
Introduction
생성 모델의 최근 발전은 이미지, 오디오, 3D 장면, 자연어 등과 같은 다양한 도메인에서 고품질의 사실적인 샘플을 합성할 수 있다는 가능성을 보여주었다. 다른 도메인에서의 성공과 달리, 고해상도 프레임에 복잡한 시공간 역학을 포함하는 동영상의 고차원성과 복잡성으로 인해 생성 품질은 아직 실제 동영상과 거리가 멀다.
복잡하고 대규모 이미지 데이터셋을 처리하는 diffusion model의 성공에 영감을 받아 최근 접근 방식은 동영상용 diffusion model 설계를 시도했다. 이미지 도메인과 유사하게, 이러한 방법은 확장성(공간 해상도와 시간 지속 시간 측면 모두)으로 동영상 분포를 훨씬 더 잘 모델링할 수 있는 큰 잠재력을 보여주었고 심지어 사실적인 생성 결과를 달성했다. 그러나 diffusion model은 샘플을 합성하기 위해 입력 공간에서 많은 반복 프로세스를 필요로 하기 때문에 심각한 계산 및 메모리 비효율로 인해 어려움을 겪는다. 이러한 병목 현상은 3차원 RGB 배열 구조로 인해 동영상에서 훨씬 더 증폭된다.
한편, 이미지 생성의 최근 연구는 diffusion model의 계산 및 메모리 비효율성을 피하기 위해 latent diffusion model을 제안했다. 픽셀 레벨에서 모델을 학습시키는 대신 latent diffusion model은 먼저 오토인코더를 학습시켜 이미지를 간결하게 매개변수화하는 저차원 잠재 공간을 학습한 다음 이 latent 분포를 모델링한다. 흥미롭게도 이 접근 방식은 state-of-the-art 생성 결과를 달성하는 동시에 샘플 합성 효율성의 극적인 개선을 보여주었다. 그러나 매력적인 잠재력에도 불구하고 동영상에 대한 latent diffusion model의 한 형태를 개발하는 것은 아직 간과되고 있다.

본 논문은 동영상을 위한 새로운 latent diffusion model인 projected latent video diffusion model (PVDM)을 제안한다. 구체적으로 보면 두 단계의 프레임워크이다.
Autoencoder. 동영상의 복소 3차원 배열 구조를 인수분해하여 3개의 2D 이미지와 같은 잠재 벡터로 동영상을 표현하는 오토인코더를 소개한다. 구체적으로, 3D 픽셀을 3개의 간결한 2D latent 벡터로 인코딩하기 위해 각 시공간 방향에서 동영상의 3D → 2D 프로젝션을 제안한다. 높은 레벨에서 동영상의 공통 콘텐츠(ex. 배경)를 parameterize하기 위해 시간 방향에 걸쳐 하나의 latent 벡터를 디자인하고 동영상의 움직임을 인코딩하기 위해 나머지의 두 벡터를 디자인한다. 이러한 2D latent 벡터는 동영상의 고품질의 간결한 인코딩을 달성하는 데 도움이 될 뿐만 아니라 이미지와 같은 구조로 인해 계산 효율적인 diffusion model 아키텍처 설계를 가능하게 한다.
Diffusion model. 동영상 오토인코더에서 구축한 2D 이미지와 같은 latent space를 기반으로 동영싱 분포를 모델링하기 위한 새로운 diffusion model 아키텍처를 디자인한다. 동영상을 이미지와 같은 latent 표현으로 parameterize하기 때문에 동영상 처리에 일반적으로 사용되는 계산량이 많은 3D convolutional network 아키텍처를 사용하지 않는다. 대신 이미지 처리에 강점을 보인 2D convolutional diffusion model 아키텍처를 기반으로 한다. 또한 임의 길이의 긴 동영상을 생성하기 위한 unconditional 생성 및 프레임 조건부 생성 모델링의 공동 학습을 제시한다.
Projected latent video diffusion model
저자들은 먼저 동영상 생성 모델링의 문제를 공식화한다. 데이터셋 \(\mathcal{D} = \{x_i\}_{i=1}^N\)을 고려할 때 각 $x \in \mathcal{D}$가 모르는 데이터 분포 $p_\textrm{data} (x)$에서 샘플링된다. 각 $x \in \mathbb{R}^{3 \times S \times H \times W}$는 $S$ 프레임으로 구성된 $H \times W$ 해상도의 동영상 클립이다. 동영상 생성 모델링에서 본 논문의 목표는 $\mathcal{D}$를 사용하여 모델 분포 $p_\textrm{model} (x)$를 $p_\textrm{data} (x)$로 매칭하는 것이다.
이 목표를 달성하기 위하여 diffusion model을 기반으로 하는 방법을 구축한다. Diffusion model은 mode collapse 문제 없이 고품질 샘플을 합성하며 복잡한 데이터셋을 잘 모델링한다. 하지만, diffusion model은 input space에서 바로 연산되기 때문에 동영상을 위해 디자인하기 어렵다. 이를 해결하기 위해 새로운 저차원 latent space에서 연산을 하며, 이 latent space는 동영상 픽셀의 복잡한 3D 구조를 3개의 2D 구조로 나누어 간결하게 동영상을 parameterize한다.
1. Latent diffusion models
높은 레벨에서 diffusion model은 점진적인 denoising process를 통해 $p_\textrm{data} (x)$를 학습한다. Diffusion model은 고정된 길이 $T > 0$의 Markov diffusion process $q(x_t \vert x_{t-1})$의 reverse process $p_\theta (x_{t-1} \vert x_t)$를 고려한다. 미리 정의된 $0 < \beta_1, \cdots, \beta_T < 1$에 대하여 다음과 같은 정규 분포로 나타낼 수 있다.
\[\begin{equation} q(x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I_x) \\ q(x_t \vert x_0) = \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha}_t} x_0, (1-\bar{\alpha}_t)I_x) \\ \bar{\alpha}_t := \prod_{i=1}^t (1 - \beta_i) \end{equation}\]Reparameterization trick을 사용하면 $p_\theta (x_{t-1} \vert x_t)$를 denoising autoencoder $\epsilon_\theta (x_t, t)$로 학습할 수 있으며, $\epsilon_\theta (x_t, t)$는 다음과 같은 noise 예측 목적 함수로 학습된다.
\[\begin{equation} \mathbb{E}_{x_0, \epsilon, t} [\| \epsilon - \epsilon_\theta (x_t, t) \|_2^2] \\ x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]또한 $p_\theta (x_{t-1} \vert x_t)$는 다음과 같이 충분히 작은 $\beta_t$에 대한 정규 분포로 근사할 수 있다.
\[\begin{equation} p_\theta (x_{t-1} \vert x_t) := \mathcal{N} \bigg( x_{t-1}; x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t), \sigma_t^2 \bigg) \end{equation}\]분산 $\sigma_t^2 := \beta_t$는 미리 정의된 hyperparameter이다.
Diffusion model의 주요 단점은 심각한 계산 및 메모리 비효율성이다. 샘플을 생성하기 위해서는 $p_\theta (x_{t-1} \vert x_t)$를 고차원 input space $\mathcal{X}$에서 반복적으로 연산해야 한다. 이 문제를 해결하기 위해 간결하게 데이터를 인코딩하는 저차원 latent space $\mathcal{Z}$에서 분포를 학습하는 latent diffusion model이 제안되었다. Latent diffusion model은 denoising autoencoder $\epsilon_\theta (z_t, t)$를 $\mathcal{Z}$에서 학습하므로 먼저 $z$를 샘플링한 뒤 디코더를 사용하여 $z$로 디코딩한다. $x$에서 $z$로의 상당한 차원 감소로 인하여 데이터 샘플링을 위한 계산이 굉장히 줄어든다. 저자들은 여기에 영감을 받아 동영상 분포를 latent diffusion model로 모델링한다.
2. Designing efficient latent video diffusion model
Autoencoder
동영상 $x$를 저차원 latent 벡터 $z$로 표현하기 위해서 인코더 $f_\phi : \mathcal{X} \rightarrow \mathcal{Z}$와 디코더 $g_\psi : \mathcal{Z} \rightarrow \mathcal{X}$로 구성된 오토인코더를 학습시킨다. VQGAN과 같이 픽셀 레벨의 reconstruction loss와 LPIPS의 negative를 더한 loss를 최소화하여 동영상을 discrete latent code로 인코딩한다.
기존의 동영상 오토인코더는 frame-wise 2D convolutional network나 3D convolutional network에 대부분 의존하여 주어진 동영상을 압축한다. 이 접근 방식들이 효과적으로 $x$를 저차원으로 인코딩하지만, $x$를 3D latent 벡터로 인코딩하는데 시간적 일관성을 간과하며 3D 텐서를 처리하기 위해 diffusion model 아키텍처가 필요하고 계산 오버헤드가 발생할 수 있다.
대신에 저자들은 다른 접근 방식을 사용한다. $x$가 주어지면 $z$를 3개의 2D latent 벡터 $z^s$, $z^h$, $z^w$로 구성한다.
\[\begin{equation} z := [z^s, z^h, z^w], \quad \quad z^s \in \mathbb{R}^{C \times H' \times W'}, \\ z^h \in \mathbb{R}^{C \times S \times W'}, \quad \quad z^w \in \mathbb{R}^{C \times S \times H'} \end{equation}\]$C$는 latent 차원이며, $H’ = H/d, W’ = W/d$이다 $(d > 1)$. $z^s$, $z^h$, $z^w$는 각각 \(z_{hw}^s, z_{sw}^h, z_{sh}^w \in \mathbb{R}^C\)을 concat한 것이다.
$z^s$는 $x$에서 시간 축에 걸쳐 공통 컨텐츠를 포착하도록 디자인되었으며, $z^h$와 $z^w$는 동영상의 두 공간 축에 걸쳐 표현을 학습하여 $x$의 기본 모션을 인코딩한다. $[z^s, z^h, z^w]$는 인코더 $f_\phi$로 계산되며, $f_\phi$는 video-to-3D-latent mapping \(f_{\phi_{shw}}^{shw}\)와 3D-to-2D latent projection \(f_{\phi_s}^s \times f_{\phi_h}^h \times f_{\phi_w}^w\)의 결합이다. (아래 그림 참고)

구체적으로, 다음과 같이 $x$에서 $z$를 계산한다.
디코더 $g_\psi$는 $z$에서 3D latent grid $v$를 계산하고 $v$에서 $x$를 복원한다. $v$는 다음과 같이 계산된다.
\[\begin{equation} v = (v_{shw}) \in \mathbb{R}^{3C \times S \times H' \times W'} \\ v_{shw} := [z_{hw}, z_{sw}, z_{sh}] \end{equation}\]본 논문에서는 \(f_{\phi_{shw}}^{shw}\)와 $g_\psi$를 위해 동영상 Transformer를 사용하고 \(f_{\phi_s}^s \times f_{\phi_h}^h \times f_{\phi_w}^w\)를 위해 작은 Transformer를 사용한다.
오토인코더 디자인은 추가 프로젝션에서 동영상을 인코딩하기 위해 약간 더 많은 파라미터와 계산이 필요하지만 latent space에서 diffusion model의 학습과 샘플링을 위한 극적인 계산 효율성을 제공한다. 특히, 기존 동영상 오토인코더 는 $O(SHW)$ 차원의 latent code가 인코딩을 위해 필요하므로 3D convolution layer와 self-attention layer를 활용하기 위한 diffusion model이 필요하고, 이는 각각 계산 오버헤드가 $O(SHW)$와 $O((SHW)^2)$이다.
반면, 본 논문은 동영상을 $O(HW + SW + SH)$개의 latent code를 사용하여 이미지와 같은 latent 벡터로 표현한다. 이러한 latent 표현은 이미지 diffusion model에 사용되는 2D convolution layer ($O(HW + SW + SH)$)와 self-attention layer ($O((HW + SW + SH)^2)$)를 활용하여 보다 계산 효율적인 diffusion model 디자인이 가능하다.
전체 오토인코더 디자인의 이면에 있는 직관은 비디오가 시간적으로 일관된 신호이며 시간 축에서 공통 콘텐츠를 공유한다는 것이다. 일반적인 콘텐츠를 $z^s$로 캡처하면 비디오 인코딩을 위한 매개변수의 수를 크게 줄일 수 있다. 또한 비디오의 높은 시간적 일관성으로 인해 시간적 변동이 그다지 크지 않은 경우가 많다. 저자들은 2개의 공간 그리드로 동작의 간결한 표현을 경험적으로 검증하며, $z^h$, $z^w$는 인코딩 품질을 손상시키지 않는다.
Latent diffusion model
$[z^s, z^h, z^w]$에 대하여 denoising autoencoder를 학습하기 위하여 2D convolutional U-Net 아키텍처를 기반으로 신경망을 디자인한다. 구체적으로, $z^s$, $z^h$, $z^w$을 denoise하기 위해 공유 U-Net 1개를 사용한다. $z^s$, $z^h$, $z^w$ 간의 종속성을 처리하기 위해 공유 U-Net에서 $z^s$, $z^h$, $z^w$의 중간 feature에 대해 작동하는 attention layer를 추가한다. 이러한 2D convolution 아키텍처 디자인은 동영상용 naive한 3D convolution U-Net보다 계산 효율적이다. 이는 “이미지와 같은” 구조와 적은 latent code를 사용하여 축소된 latent 벡터의 차원으로 인해 가능하다.
3. Generating longer videos with PVDM
동영상은 순차적인 데이터이다. 모든 동영상 $x \in \mathcal{D}$의 길이 $S$가 같다고 가정하는 세팅과 달리 실제 비디오의 길이는 다양하며 생성 비디오 모델은 임의 길이의 비디오를 생성할 수 있어야 한다. 그러나 고정 길이의 동영상 클립 $p_\textrm{data} (x)$의 분포만 학습한다. 긴 비디오 생성을 가능하게 하기 위해 두 개의 연속 비디오 클립 $[x^1, x^2]$의 조건부 분포 $p (x^2 \vert x^1)$ 학습하고 현재 클립이 주어진 미래 클립을 순차적으로 생성하는 것을 고려할 수 있다.
직접적인 해결책은 unconditional 분포 $p_\textrm{data} (x)$와 conditional 분포 $p(x^2 \vert x^1)$를 학습하기 위해 두 개의 개별 모델을 갖는 것이다. 저자들은 추가 모델을 사용하는 대신 두 분포를 공동으로 학습하기 위해 단일 diffusion model을 학습할 것을 제안한다. $p(x)$의 공동 학습을 위한 null frame을 도입하여 conditional diffusion model $p(x^2 \vert x^1)$를 학습함으로써 달성할 수 있다. 보다 구체적으로, 다음과 같은 목적 함수로 latent space에서 denoising autoencoder $\epsilon_\theta (z_t^2, z_0^1, t)$의 학습을 고려한다.
\[\begin{equation} \mathbb{E}_{(x_0^1, x_0^2), \epsilon , t} [\lambda \| \epsilon - \epsilon_\theta (z_t^2, z_0^1, t) \|_2^2 + (1-\lambda) \| \epsilon - \epsilon_\theta (z_t^2, 0, t) \|_2^2] \\ z_0^1 = f_\phi (x_0^1), z_0^2 = f_\phi (x_0^2), z_t^2 = \sqrt{\vphantom{1} \bar{\alpha}_t} z_0^2 + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]$\lambda \in (0,1)$은 두 분포의 균형을 맞추는 hyperparameter이다.
학습 후에 다음과 같이 긴 동영상을 생성할 수 있다. 초기 동영상 클립 $x^1 \sim p_\theta (x)$를 샘플하고, 이전 클립으로 컨디셔닝하여 다음 클립 $x^{l+1} \sim p_\theta (x^{l+1} \vert x^l)$을 생성하는 것을 반복한다. 마지막으로 모든 생성된 클립을 concat하여 긴 동영상을 만든다. 다음은 자세한 내용을 포함한 전체 알고리즘이다.

Experiments
- 데이터셋: UCF-101, SkyTimelapse (16 / 128 frames, 256$\times$256 해상도)
- 오토인코더: 인코더와 디코더 모두 TimeSformer, Adam으로 학습
- Diffusion model: Transformer, AdamW으로 학습
1. Main results
Qualitative results
다음은 UCF-101과 SkyTimelapse에서의 16 프레임 동영상 합성 결과이다. (a)는 작은 물체의 움직임을 포함하며, (b)는 전체 프레임의 큰 전환을 포함한다. (Stride 2)

Quantitative results
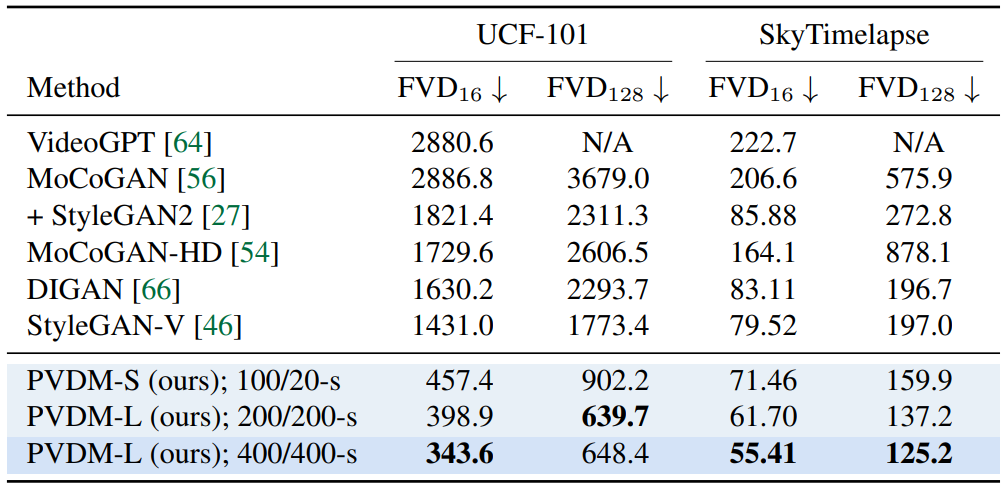
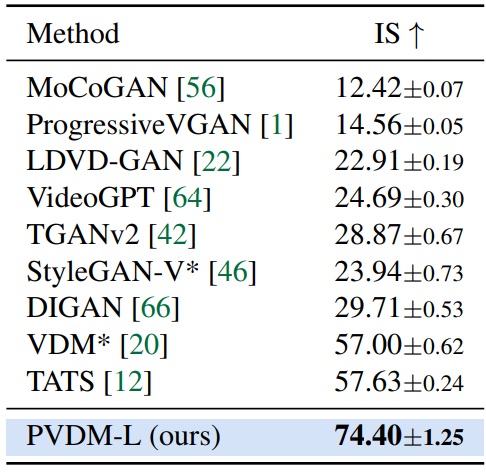
다음은 PVDM과 기존 동영상 생성 방법간의 정량적 비교 결과이다. $N/M$-s는 처음 클립은 $N$ step으로, 나중 클립은 $M$ step으로 DDIM 샘플러를 사용한 것을 의미한다.
Long video generation
다음은 PVDM의 128 프레임 동영상 합성 결과이다.

2. Analysis
Reconstruction quality
다음은 UCF-101과 SkyTimelapse에서 학습된 오토인코더의 복원 결과이다. (Stride 4)

다음은 실제 동영상과 PVDM의 오토인코더로 복원한 동영상 사이의 정량적 평과 결과이다.

Comparison with VDM
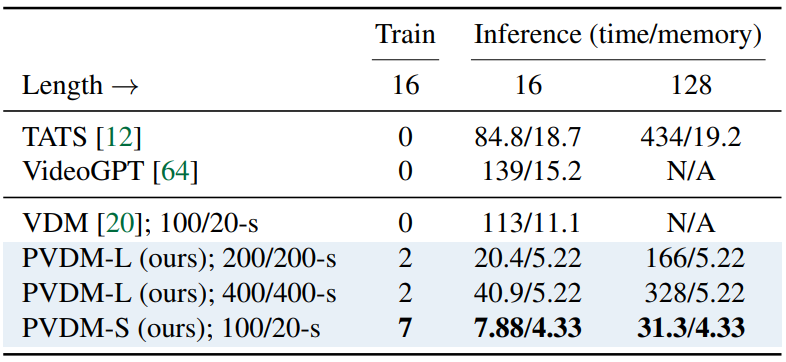
다음은 NVIDIA 3090Ti 24GB GPU 1개에 대하여 학습을 위한 최대 batch size와 합성 시 소용되는 시간과 메모리를 측정한 것이다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)