NeurIPS 2021. [Paper] [Page] [Github]
Abhishek Sinha, Jiaming Song, Chenlin Meng, Stefano Ermon
Department of Computer Science, Stanford University
6 Dec 2022
Introduction
레이블이 없는 대량의 데이터에 대해 학습된 생성 모델은 다양한 영역에서 큰 성공을 거두었다. 그러나 생성 모델의 다운스트림 애플리케이션은 다양한 컨디셔닝을 기반으로 하는 경우가 많다. 조건부 모델을 직접 학습시키는 것이 가능하지만 이를 위해서는 많은 양의 쌍으로 된 데이터가 필요하며, 이를 얻기 위해 많은 비용이 소모된다. 따라서 많은 양의 레이블이 없는 데이터와 가능한 적은 쌍으로 된 데이터를 사용하여 조건부 생성 모델을 학습하는 것이 바람직하다.
Contrastive self-supervised learning (SSL) 방법은 레이블이 없는 데이터로부터 효과적인 표현을 학습하여 식별 task에서 레이블이 없는 데이터의 필요성을 크게 줄일 수 있으며, few-shot learning을 개선하는 것으로 나타났다. 따라서 few-shot 생성을 개선하는 데에도 SSL을 사용할 수 있는지 묻는 것은 당연하다. Latent Variable Generative Models (LVGM)은 생성하는 데이터의 저차원 latent 표현을 이미 포함하고 있기 때문에 이에 대한 후보이다. 그러나 GAN이나 diffusion model과 같이 널리 사용되는 LVGM에는 입력을 표현에 매핑하는 명시적이고 tractable한 함수가 없기 때문에 SSL로 잠재 변수를 최적화하기가 어렵다. 반면 VAE는 인코더 모델을 통해 자연스럽게 SSL을 채택할 수 있지만 일반적으로 샘플 품질이 더 나쁘다.
본 논문에서는 조건부 few-shot 생성에 적합한 특별한 VAE인 Diffusion-Decoding models with Contrastive representations (D2C)을 제안한다. D2C는 contrastive SSL 방법을 사용하여 self-supervised 표현의 전송 가능성과 few-shot 능력을 가지는 latent space를 얻는다. 다른 VAE와 달리 D2C는 latent 표현에 대한 diffusion model을 학습한다. 이 latent diffusion model은 D2C가 학습과 생성 모두에 대해 동일한 latent 분포를 사용하도록 한다.
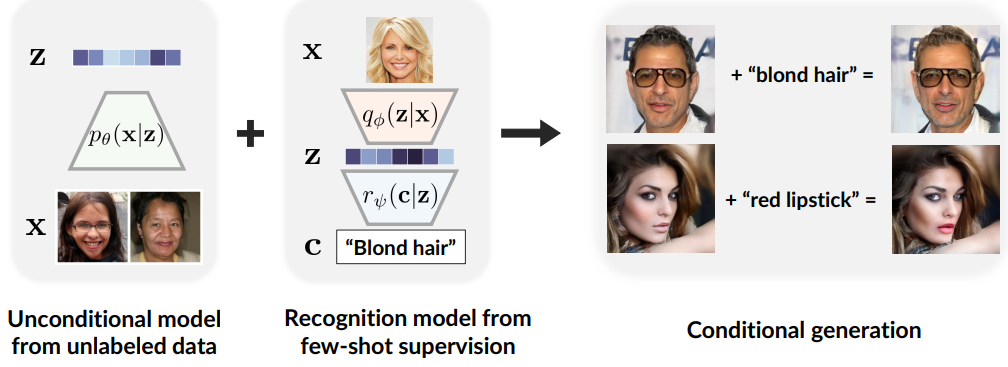
저자들은 이 접근법이 기존의 계층적 VAE보다 더 나은 샘플 품질로 이어질 수 있는 이유를 설명한다. 레이블이 지정된 예제나 조작 제약 조건을 통해 조건이 정의되는 조건부 생성에 D2C를 적용하는 방법에 대해 자세히 설명한다. 이 접근 방식은 컨디셔닝을 제공하는 식별 모델과 latent space에 대한 generative diffusion model을 결합하며 이미지 space에 직접 작용하는 방법보다 계산적으로 더 효율적이다. (위 그림 참고)
Problem Statement
기존의 많은 방법은 일부 알려진 조건에 최적화되어 있거나 사전 학습에 사용할 수 있는 이미지와 조건 사이에 풍부한 쌍을 가정한다. 본 논문에서는 쌍을 이룬 데이터에 대해 학습하지 않는다. 고품질의 latent 표현이 unconditional한 이미지 생성에 필수적인 것은 아니지만 SSL 표현이 다운스트림 task에서 라벨링 작업을 줄이는 것과 유사하게 제한된 supervision으로 특정 조건을 지정하려는 경우 유용할 수 있다. 강력한 사용 사례는 이미지 조작을 통해 데이터셋의 편향을 감지하고 제거하는 것이다. 여기서 우리는 잘 알려진 편향을 해결할 뿐만 아니라 예측하기 어려운 다른 편향을 사회적 요구에 맞게 조정해야 한다.
따라서 바람직한 생성 모델은 샘플 품질이 높을 뿐만 아니라 유용한 latent 표현도 포함해야 한다. VAE는 인코더 내에 SSL을 통합할 수 있기 때문에 풍부한 latent 표현을 학습하는 데 이상적이지만 일반적으로 GAN이나 diffusion model과 동일한 수준의 샘플 품질을 달성하지 못한다.
Diffusion-Decoding Generative Models with Contrastive Learning
위의 문제를 해결하기 위해 고품질 샘플과 고품질 latent 표현이 있는 VAE의 확장인 D2C를 제시하므로 few-shot 조건부 생성에 매우 적합하다. 또한 GAN 기반 방법과 달리 D2C는 불안정한 적대적 훈련을 포함하지 않는다. (아래표 참고)

이름에서 알 수 있듯이 D2C의 생성 모델에는 두 가지 구성 요소 diffusion과 decoding이 있다. Diffusion 요소는 latent space에서 연산을 하고 decoding 요소는 latent 표현을 이미지로 매핑한다. $\alpha$를 diffusion 랜덤 변수로 사용한다 $z^({0}) \sim p^{(0)} (z^{(0)}) := \mathcal{N}(0,I)$는 $\alpha = 0$인 noisy한 latent 변수이고, $z^{(1)}$은 $\alpha = 1$인 깨끗한 latent 변수이다. D2C의 생성 프로세스는 $p_\theta (x \vert z^{(0)})$으로 나타내며 다음과 같이 정의된다.
즉, D2C 모델은 diffusion process로 $z^{(1)}$을 만들고 $x$로 디코딩한다.
D2C 모델을 학습하기 위하여, inference model $q_\phi (z^{(1)} \vert x)$를 사용하여 $x$의 적합한 latent 변수 $z^{(1)}$을 예측한다. 이 모델은 SSL 방법을 바로 통합할 수 있으며 다음 목적 함수로 나타낼 수 있다.
\[\begin{aligned} L_\textrm{D2C} (\theta, \phi; w) & := L_\textrm{D2} (\theta, \phi; w) + \lambda L_\textrm{C} (q_\phi) \\ L_\textrm{D2} (\theta, \phi; w) & := \mathbb{E}_{x \sim p_\textrm{data}, z^{(1)} \sim q_\phi (z^{(1)} \vert x)} [-\log p(x \vert z^{(1)}) + l_\textrm{diff} (z^{(1)}; w, \theta)] \\ l_\textrm{diff} (x; w, \theta) & := \sum_{i=1}^T w(\alpha_i) \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} [\| \epsilon - \epsilon_\theta (x^{(\alpha_i)}, \alpha_i) \|_2^2] \\ x^{(\alpha_i)} & := \sqrt{\alpha_i} x + \sqrt{1 - \alpha_i} \epsilon \end{aligned}\]$L_\textrm{C} (q_\phi)$는 풍부한 data augmentation을 포함하는 임의의 contrastive predictive coding objective이고, $\lambda > 0$는 가중치 hyperparameter이다. $L_\textrm{D2}$는 reconstruction loss와 diffusion loss를 포함한다.
D2C의 생성 모델과 inference 모델은 아래 그림과 같다.

1. Relationship to maximum likelihood
$L_\textrm{D2}$는 VAE의 목적 함수와 비슷하다. $L_\textrm{D2}$는 log-likelihood의 variational lower bound와 깊게 연결되어 있다.
Theorem 1. 임의의 가능한 \(\{\alpha_i\}_{i=1}^T\)에 대하여, $-L_\textrm{D2}$가 log-likelihood의 variational lower boundary인 가중치 \(\hat{w} : \{\alpha_i\}_{i=1}^T \rightarrow \mathbb{R}_{+}\)가 diffusion 목적 함수를 위해 존재한다.
\[\begin{aligned} -L_\textrm{D2} (\theta, \phi; \hat{w}) \le \mathbb{E}_{p_\textrm{data}} [\log p_\theta (x)] \\ p_\theta (x) := \mathbb{E}_{x_0 \sim p^{(0)} (z^{(0)})} [p_\theta (x \vert z^{(0)})] \end{aligned}\]2. D2C models address latent posterior mismatch in VAEs
저자들은 D2C는 VAE의 특수한 경우이지만 VAE 방법의 오랜 문제, 즉 사전 확률 분포 $p_\theta (z)$와 사후 확률 분포 \(q_\phi (z) := \mathbb{E}_{p_\textrm{data}} (x)\) 간의 불일치를 해결한다는 점에서 D2C가 사소하지 않다고 주장한다. 불일치는 사전 확률에 “구멍”을 생성할 수 있다. 즉, 사후 확률이 학습 중에 커버하지 못하여 생성 중에 사용된 많은 latent 변수가 학습되지 않았을 가능성이 높기 때문에 샘플 품질이 나빠진다. 다음 정의에서 이 개념을 공식화합니다.
Definition 1 (Prior hole). $p(z)$와 $q(z)$를 $\textrm{supp}(q) \subseteq \textrm{supp}(p)$인 분포라고 하자. 집합 $S \in \textrm{supp}(P)$일 때, $q$가 $p$에 대하여 $\int_S p(z)dz \ge \delta$이고 $\int_S q(z)dz \le \epsilon$인 $(\epsilon, \delta)$-prior hole을 가진다고 한다. ($\epsilon$, $\delta$ \in (0, 1), $\delta > \epsilon$)
직관적으로 $q_\phi (z)$에 큰 $\delta$와 작은 $\epsilon$의 prior hole이 있는 경우(ex. 학습 샘플 수에 반비례) prior hole 내의 latent 변수는 학습 중에 절대 표시되지 않을 가능성이 크지만 ($\epsilon$가 작음) 샘플을 생성하는 데 자주 사용된다 ($\delta$가 큼).
대부분의 기존 방법은 KL-divergence나 Wasserstein 거리와 같은 특정 통계적 발산을 최적화하여 이 문제를 해결한다. 그러나 특히 $q_\phi (z)$가 매우 유연할 때 특정 발산 값을 합리적으로 낮게 최적화하더라도 prior hole이 제거되지 않을 수 있다.
Theorem 2. $p_\theta (z) = \mathcal{N}(0,I)$라 하자. 임의의 $\epsilon > 0$과 $\gamma > 0$에 대하여 $D_\textrm{KL} (q_\phi || p_\theta ) \le \log 2$이고 $W_2 (q_\phi, p_\theta)$인 $(\epsilon, 0.49)$-prior holde를 가진 $q_\phi (z)$가 존재한다.
최적화에 의해 prior hole을 처리하는 것과는 대조적으로 diffusion model은 $z^{(1)}$에서 $z^{(0)}$까지의 diffusion process는 $\alpha \rightarrow 0$일 때 $z^{(\alpha)}$가 항상 표준 가우시안으로 수렴하도록 구성되기 때문에 prior hole을 제거한다. 결과적으로 학습 중에 사용되는 latent 변수의 분포는 생성에서 사용되는 분포와 임의로 근접하며 GAN에서도 마찬가지이다. 따라서 저자들의 주장은 VAE와 NF보다 GAN이나 diffusion model에서 더 나은 샘플 품질 결과를 관찰하는 이유에 대한 설명을 제공한다.
Few-shot Conditional Generation with D2C
Algorithm

Algorithm 1은 몇 개의 이미지에서의 조건부 생성을 위한 일반적인 알고리즘을 설명한다. Latent space $r_\psi (c \vert z^{(1)})$에 대한 모델을 사용하여 diffusion prior로 비정규화 분포에서 조건부 latent를 만든다. 이는 rejection sampling이나 Langevin dynamics와 같은 다양한 방식으로 구현될 수 있다.
Conditions from labeled examples
레이블이 지정된 몇 가지 예시가 주어지면 특정 레이블로 다양한 샘플을 생성하려고 한다. 레이블이 지정된 예시의 경우 latent space에 대해 clasifier를 직접 학습할 수 있다. 이를 $r_\psi (c \vert z^{(1)})$로 표시하고 $c$는 클래스 레이블이고 $z^{(1)}$은 $x$의 latent 표현이다. 이러한 예제에 레이블이 없는 경우, 새 예제에 “positive”를 지정하고 학습 데이터에 “unlabeled”를 지정하는 positive-unlabeled (PU) classifier를 학습할 수 있다. 그런 다음 diffusion model과 함께 classifier를 사용하여 $z^{(1)}$의 적합한 값을 생성한다.
Conditions from manipulation constraints
레이블이 지정된 몇 가지 예시가 주어지면 이미지를 조작하는 방법을 배우고자 한다. 특히 “$x$는 레이블 $c$를 갖지만 이미지 $\bar{x}$와 유사하다”라는 이벤트에 대해 컨디셔닝한다. 여기서 $r_psi (c \vert z^{(1)})$는 classifier 조건부 확률과 latent $\bar{z}^{(1)}$의 정확도 사이의 비정규화 곱이다. Algorithm의 라인 4를 Lanvegin과 유사한 절차로 구현한다. 여기서 classifier 확률에 대해 gradient step을 수행한 다음 diffusion model로 이 gradient step을 수정한다. 많은 GAN 기반 방법과 달리 D2C는 평가 시 inversion 절차를 최적화할 필요가 없으므로 latent 값 계산이 훨씬 빠르다. 또한 D2C는 reconstruction loss로 인해 원본 이미지의 fine한 특징을 더 잘 유지한다.
Experiments
1. Unconditional generation
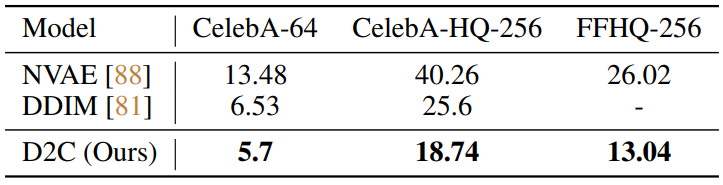
다음은 샘플 품질을 비교한 표이다. 위의 표는 생성과 표현의 품질을 측정한 표이고, 아래 표는 다양한 얼굴 데이터셋에 대한 FID를 측정한 표이다.

다음은 diffusion step에 따른 샘플 품질을 비교한 표이다.

다음은 CIFAR-10 (왼쪽), fMoW (중간), FFHQ (오른쪽)에서 생성된 샘플들이다.

2. Few-shot conditional generation from examples
다음은 레이블에 따른 few-shot 조건부 생성의 FID를 측정한 표이다.

3. Few-shot conditional generation from manipulation constraints
저자들은 CelebA-256 데이터셋에서 두 속성 blond와 red lipstick에 대하여 Amazon Mechanical Turk (AMT) 평가를 수행하였다. 다음은 blond(위)와 red lipstick(아래)에 대한 이미지 조작 결과이다.

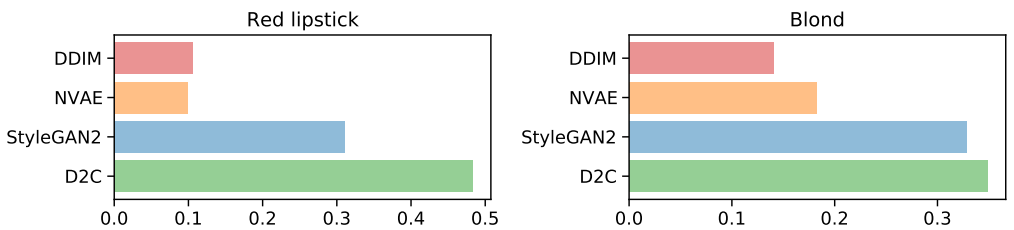
다음은 AMT 평가 결과를 나타낸 그래프이다. 4개의 모델로 생성한 이미지 중 하나를 AMT evaluator가 선택한 것이다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)