arXiv 2022. [Paper]
Eliahu Horwitz, Yedid Hoshen
School of Computer Science and Engineering, The Hebrew University of Jerusalem, Israel
17 Nov 2022

Introduction
Diffusion model은 super-resolution, inpainting, colorization과 같은 넓은 범위의 생성 task의 주요 방법이 되었다. 그러나 다른 많은 딥러닝 기반 방법과 마찬가지로 여전히 블랙박스 (기능은 알지만 작동 원리를 이해할 수 없는 복잡한 시스템)에 가깝다.
실제 고위험 상황에 diffusion model을 배치하려면 모델이 예측에 대해 갖는 신뢰도를 통계적으로 보장하는 방법이 필요하다. 이를 위해 픽셀의 실제 값이 사용자가 설정한 확률로 구간 내에 있도록 생성된 각 픽셀에 구간을 구성한다. 예를 들어 저해상도 MRI 스캔을 분석하는 의사는 해상도를 높이면 큰 이점을 얻을 수 있다. 그러나 생성 모델은 디테일을 “환각”하는 경향이 있기 때문에 의사는 최신 diffusion model로 생성된 고해상도 이미지가 실제로 현실에 충실하다는 것을 신뢰하지 못할 수 있다. 의사에게 각 픽셀 주위에 통계적으로 보장된 구간을 제공하면 생성 모델의 출력을 사용할 수 있다.
본 논문에서는 image-to-image task에서 신뢰 구간을 구성하기 위하여 diffusion model을 사용한다. Naive한 접근 방식은 diffusion model의 뛰어난 분포 근사 기능을 직접 사용할 수 있다. 입력 이미지가 주어진 모델의 여러 해에서 먼저 샘플링한다. 해 분포를 사용하여 각 픽셀의 경계를 추정한다. 저자들은 이 방법이 단순함에도 불구하고 quantile regression으로 구간을 구성하는 현재 선도적인 방법보다 더 좁은 구간을 생성한다는 것을 발견했다.
Naive한 샘플링 방법은 각 테스트 이미지에 대해 여러 샘플링된 변형이 필요하고 한 번의 inference step에 여러 denoising step이 필요하기 때문에 매우 느리다. 실제로 각 테스트 이미지에 대해 수천 개의 forward pass가 필요하다. 샘플링 병목 현상을 가속화하기 위해 inference 시간에 여러 변형을 샘플링하지 않고 단일 forward step 에서 샘플링된 범위를 근사화하는 amortized 방법을 도입한다. 불행하게도 샘플링된 범위를 근사하면 종종 최적이 아닌 간격이 생성된다.
저자들은 두 방법의 장점을 합친 Conffusion을 제안한다. 사전 학습된 diffusion model이 주어지면, quantile regression loss를 사용하여 경계 예측을 위한 finetuning을 한다. Diffusion model이 일반적으로 하나의 생성을 위해 여러 forward pass가 필요하지만, Conffusion은 단일 forward pass만 필요하다. 이는 diffusion process에서 denoising model을 분리하여 달성할 수 있다. 또한, 사전 학습된 강력한 feature들 덕분에 다른 데이터셋과 다른 task의 신뢰 구간을 추출하도록 finetuning을 할 수 있다.
Preliminaries
1. Diffusion Models
Diffusion model은 샘플링된 가우시안 noise를 데이터 분포의 샘플 $x_0$로 변환한다. 이 매핑은 $x_0$에서 $x_t$로의 noising process를 점진적으로 역전시키는 denoising 신경망 $f_\theta$를 학습시켜 수행된다. 조건부 diffusion model은 입력 신호에 대한 denoising process를 컨디셔닝한다. 특히 image-to-image diffusion model은 $x$와 $y$가 모두 이미지인 $p(y \vert x)$ denoising step을 수행한다.
Diffusion model은 $T$ denoising step을 통해 타겟 이미지 $y_0$를 생성한다. 가우시안 noise $y_T \sim \mathcal{N}(0,I)$에서 시작하여 모델은 $y_0 ~ p(y \vert x)$에 도달할 때까지 학습된 transition 분포 $p_\theta (y_{t−1} \vert y_t, x)$를 사용하여 이미지를 반복적으로 정제한다. 이 반복 프로세스는 이미지 생성에 여러 네트워크 평가가 필요하므로 시간과 컴퓨팅 집약적입니다.
대부분의 이미지 diffusion model은 denoising step을 학습하기 위해 U-Net을 사용하며, 현재 단계 $t$는 인코딩되어 $y_t$와 함께 네트워크로 전달된다. 이미지를 컨디셔닝할 때 가우시안 noise 이미지에서 시작하는 대신 입력 이미지를 일부 $t \in [0, T)$로만 diffuse하는 경우가 많으며, 이는 원래 입력 신호의 일부를 보존하기 위한 것이다.
2. Confidence Guarantees
Definitions. Calibration set을 \(\{x_i, y_i\}_{i=1}^N\)이라 표현하며, $x_i, y_i \in [0,1]^{M \times N}$은 각각 손상된 이미지와 타겟 이미지이다. 본 논문의 목표는 픽셀의 실제 값이 사용자가 설정한 확률로 구간 내에 있도록 $\hat{y}_i$의 각 픽셀에 신뢰 구간을 구성하는 것이다. 각 픽셀에 대하여 다음과 같은 구간을 구성한다.
\[\begin{equation} \mathcal{T} = \bigg[ \hat{l} (x_{i_{mn}}), \hat{u} (x_{i_{mn}}) \bigg] \end{equation}\]$\hat{l}$과 $\hat{u}$는 구간의 lower bound와 upper bound이다. 구간의 통계적 건전성을 위해 사용자는 위험 레벨 $\alpha \in (0, 1)$과 오류 레벨 $\delta \in (0, 1)$을 선택한다. 그런 다음 최소 $1-\alpha$의 ground truth 픽셀 값이 확률 $1-\delta$로 포함되도록 간격을 구성한다. 즉, 적어도 $1-\delta$의 확률로
\[\begin{equation} \mathbb{E} \bigg[ \frac{1}{MN} \bigg\| \{ (m, n) : y_{(m, n)} \in \mathcal{T} (x)_{(m, n)} \} \bigg\| \bigg] \ge 1 - \alpha \end{equation}\]이고, $x$는 테스트 샘플, $y$는 calibration set과 동일한 분포에서 얻은 레이블이다.
$\tilde{l}$과 $\tilde{u}$애 대한 명시적 가정을 하지 않았기 때문에 휴리스틱일 뿐이며 실제적인 통계적 보증을 제공하지 않는다. 이를 위해 사용자가 설정한 위험 레벨과 오류 레벨을 준수하면서 위 식을 만족하도록 $\tilde{l}$과 $\tilde{u}$를 상수 $\hat{\lambda}$로 scaling한다. 각 이미지의 각 픽셀에 대한 모든 구간의 집합을 $[\hat{\lambda} \tilde{L}, \hat{\lambda} \tilde{U}] = [\hat{L}, \hat{U}]$로 나타낸다. 이 집합을 image-valued Risk-Controlling Prediction Set라고 한다.
Definition 1 (Risk-Controlling Prediction Set (RCPS)
\[\begin{equation} \mathbb{P} (\mathbb{E} [L(\mathcal{T} (x), y)] > \alpha) \le \delta \\ L(\mathcal{T} (x), y) = 1 - \frac{\bigg\| \{ (m, n) : y_{(m, n)} \in \mathcal{T} (x)_{(m, n)} \} \bigg\|}{MN} \end{equation}\]이면, random set-valued function $\mathcal{T} : \mathcal{X} \rightarrow (2^{[0,1]})^{M \times N}$을 $(\alpha, \delta)$-Risk-Controlling Prediction Set이라고 한다.
여기서 내부의 기대값은 새로운 테스트 이미지 $(x, y)$에 대한 것이고 외부의 확률은 calibration set \(\{x_i , y_i\}_{i=1}^N\)에 대한 것이다. 위 식은 RCPS가 $\delta$의 확률로만 위험을 통제하지 못한다는 것을 의미한다.
Calibration $\tilde{l}$과 $\tilde{u}$에 대해 어떠한 가정도 하지 않았기 때문에 이 보장은 calibration process에 의해 제공된다. Calibration하는 동안 밖으로 떨어지는 픽셀 수가 $\alpha$ 미만이 되도록 가장 작은 간격을 선택한다. 저자들은 \(\mathcal{T}_\lambda = [\lambda \tilde{l}, \lambda \tilde{u}]\)가 RCPS 정의를 만족시키는 가장 작은 $\lambda$에 관심을 가졌다. 따라서 충분히 큰 $\lambda$에서 시작하여 RCPS 정의가 더 이상 충족되지 않을 때까지 반복적으로 $\mathcal{T}_\lambda$를 구성하여 calibration 상수 $\hat{\lambda}$이 된다. 본 논문에서는 $\hat{\lambda}$를 계산하기 위해 validation set를 사용하고 테스트셋에서 추출한 구간에 대한 결과를 $\lambda$로 스케일링한다.
Method
1. A Baseline for Interval Construction
최근 “im2im-uq”는 regression task를 위한 통합 구간 구성 방식을 제안하였다. im2im-uq는 입력 이미지가 주어질 때 upper bound, lower bound, reconstruction을 출력하는 신경망을 학습한다. upper bound와 lower bound를 추정하기 위하여 잘 알려진 quantile loss를 사용한다.
\[\begin{equation} \mathcal{L}_\alpha (\hat{q}_\alpha (x), y) = (y - \hat{q}_\alpha (x)) \alpha \unicode{x1D7D9} \{ y > \hat{q}_\alpha (x) \} + (\hat{q}_\alpha (x) - y) (1 - \alpha) \unicode{x1D7D9} \{ y \le \hat{q}_\alpha (x) \} \end{equation}\]$\alpha$는 최적화를 위한 quantile이고 $\hat{q}_\alpha (x)$는 quantile estimator이다. 서로 다른 quantile을 추정하기 위해 $\tilde{u}$와 $\tilde{l}$이 필요하므로 quantile loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_{QR} (x, y) = \mathcal{L}_{\alpha / 2} (\tilde{l} (x), y) + \mathcal{L}_{1- \alpha/2} (\hat{u} (x), y) \end{equation}\]최종 목적함수는 경계 추정을 위한 quantile loss와 pointwise 예측을 위한 MSE를 결합한 것이다.
\[\begin{equation} \mathcal{L} (x, y) = \mathcal{L}_{QR} (x,y) + \mathcal{L}_{mse} (x, y) \end{equation}\]학습이 끝나면 $\tilde{u}$와 $\tilde{l}$는 $1 - \alpha/2$와 $\alpha/2$에 가까워지며, 앞에서 설명한 calibration을 사용하여 최종 upper bound $\hat{u}$와 최종 lower bound $\hat{l}$을 얻는다. 이 baseline 방법은 사전 학습을 사용하지 않으며 $ADM_{UQ}$라고 부른다.
2. Sampling-based Bounds Estimation
Sampling-based Bounds
Diffusion model은 분포 근사 기능이 뛰어나기 때문에 bound 추정을 위한 자연스러운 후보이다. 따라서 사전 학습된 diffusion model의 대략적인 분포에서 샘플링하여 구간을 구성할 수 있다. 특히 특정 복원 작업(ex. super-resolution, inpainting)에 대해 학습된 diffusion model이 주어지면 손상된 각 calibration 항목 $x_i$에 대해 여러 재구성된 변형 \(SV_i = \{ \hat{y_i}_j \}_{j=1}^J\)을 샘플링하여 이미지 분포를 근사화한다. $SV_i$에서 각 픽셀의 upper bound와 lower bound의 quantile을 얻어 구간의 bound를 추출한다.
예를 들어, $\alpha = 0.1$이라고 가정하면 $\tilde{l} = \alpha / 2 = 0.05$와 $\tilde{u} = 1 − \alpha / 2 = 0.95$가 초기 간격의 bound로 둔다. 모든 이미지에서 추출한 bound $\tilde{U}, \tilde{L}$의 집합을 사용하여 $\hat{\lambda} \tilde{U} = \hat{U}$와 $\hat{\lambda} \tilde{L} = \hat{L}$이 되도록 $\hat{\lambda}$를 선택한다. Inference 시 새로운 손상된 입력 $x$가 주어지면 샘플링된 $SV$를 구성하고 $\tilde{u}, \tilde{l}$을 추출한다. 마지막으로 calibration 단계에서 $\hat{\lambda}$를 사용하여 $\hat{u}$와 $\hat{l}$을 반환한다.
이 방법은 $ADM_{UQ}$로 구성한 것보다 더 엄격한 범위를 생성하며 이를 $DM_{SB}$라고 한다. 그러나 샘플링을 통해 범위를 추정하는 것이 $ADM_{UQ}$를 능가하지만 calibration과 inference 중에 각 항목의 여러 변형을 샘플링해야 한다. 각 변형을 생성하기 위해 여러 denoising step이 필요하다는 점을 감안할 때 1개의 inference 이미지에 대한 범위를 추출하려면 수천 번의 forward pass가 필요하므로 실제 사용이 불가능하다.
Accelerating Sampled Bounds
$DM_{SB}$가 좁은 간격을 생성하므로 저자들은 간단한 가속화 방법을 제안한다. $DM_{SB}$와 비슷하게 특정 복구 task를 위해 학습된 diffusion model이 주어지면 $SV_i$를 구성하고 bound들의 집합 \(\tilde{U}_{sv}\)와 \(\tilde{L}_{sv}\)을 추출한다. Inference를 빠르게 하기 위하여 원본 diffusion model이 주어진 입력 이미지 $x_i$에 대하여 단일 forward step으로 $\tilde{u}_i$와 $\tilde{l}_i$를 예측하도록 finetuning을 한다. 구체적으로, 사전 학습된 diffusion model을 $\mathcal{DM}$으로 표시할 때 finetuning 목적 함수는 다음과 같다.
\[\begin{equation} \mathcal{L} (x, \tilde{l}_{sv}, \tilde{u}_{sv}) = \mathcal{L}_{mse} (\mathcal{DM} (x), \tilde{l}_{sv}) + \mathcal{L}_{mse} (\mathcal{DM} (x), \tilde{u}_{sv}) \end{equation}\]단일 forward pass로 샘플링된 경계를 근사화할 수 있다는 것은 diffusion의 원래 목적을 우회하는 것처럼 보인다. 그러나 이 성공이 목적 함수의 완화에 기인한다고 추측한다. Diffusion process는 높은 수준의 fidelity와 디테일을 허용하고 구간의 bound가 대부분 낮은 주파수를 포함하므로 단일 step에서 생성하기가 더 쉽기 때문에 높은 주파수 생성에 탁월하다. $DM_{SB}$와 달리 여기에서는 finetuning과 validation set 모두에 대한 bound들의 집합을 구성한다. 이 방법을 $DM_{SBA}$로 표시한다.
3. Conffusions
샘플링된 bound들을 가속화하는 것이 합리적인 결과를 생성하지만, 여전히 많은 forward step이 calibration set 구성에 필요하다. 또한, 원래의 샘플링 방법과 동일한 성능에 도달하지 못할 수 있다. 이 차이를 좁히기 위하여 본 논문에서는 quantile regression (QR)을 diffusion model에 적용하여 두 방법의 장점을 모두 가진 Conffusion을 제안한다.
Narrow Conffusion (N-Conffusion)
$DM_{SBA}$에서 사용되는 샘플링된 bound들의 근사값을 QR로 바꾼다. 특히, 특정 복원 task를 위해 학습된 diffusion model이 주어지면 \(\mathcal{L}_{QR}\)로 모델을 finetuning한다. 이는 사전 학습된 denoising model의 강력한 분포 이해와 QR의 간단한 목표를 결합한다. 또한 계산적으로 까다로운 diffusion process에서 denoising model을 분리한다. N-Conffusion은 $DM_{SBA}$의 속도를 유지하면서 간격 크기 측면에서 $DM_{SB}$를 능가하므로 단일 step 간격 구성이 가능하다.
Global Conffusion (G-Conffusion)
N-Conffusion은 이전에 논의된 모든 방법보다 성능이 우수하지만 특정 task에 대한 특정 데이터 양식과 관련된 diffusion model이 필요하다. Diffusion model은 학습시키기 어렵고 많은 양의 컴퓨팅과 데이터가 필요하다는 제한점이 있다.
따라서 저자들은 Conffusion 데이터와 task에 구애받지 않는 간단한 확장 버전인 G-Conffusion을 제안한다. Task별 모델을 사용하는 대신 일반적인 이미지 생성을 위해 미리 학습된 대규모 diffusion model을 사용한다. 특히 ImageNet에서 사전 학습된 ADM (Guided Diffusion)을 사용한다. \(\mathcal{L}_{QR}\)로 ADM을 finetuning하여 사전 학습된 하나의 모델에서 여러 task를 수행할 수 있다. 이를 통해 새로운 task와 데이터 양식을 위한 특수 모델 개발에 대한 비용을 절감할 수 있다.
Experiments
- 평가 지표
- Empirical Risk (error): 예측된 구간 밖의 픽셀값의 비율을 계산
- Interval Size: 평균 간격 크기 (작을수록 좋음)
- Size-stratified Risk: 픽셀을 간격 크기의 quartile로 나누고 각 quantile에 대한 empirical risk를 평가. (막대 그래프로 시각화되며 막대의 높이가 서로 비슷할수록 좋음)
- Model
- Super-resolution: FFHQ에서 사전 학습한 SR3 모델을 사용하여 16$\times$16 → 128$\times$128을 수행
- Inpainting: CelebA-HQ에서 사전 학습한 Palette를 사용하여 256$\times$256 이미지의 중앙 128$\times$128 영역의 inpainting 수행
- 샘플링: 각 이미지마다 200개씩 샘플링. 속도를 올리기 위해 200 step의 cosine scheduler 사용.
- G-Conffusion의 경우 ImageNet에서 사전 학습한 128$\times$128 ADM 모델 사용.
- Data
- CelebA-HQ의 테스트 셋을 1000(finetuning)/200(validation)/800(test)로 나누어 사용
- validation은 $\hat{\lambda}$ 계산과 hyperparameter 탐색에 사용
- validation set에서 계산된 $\hat{\lambda}$를 test set에 사용하여 평가
- Intervals: $\alpha = \delta = 0.1$
1. Super-resolution
다음은 super-resolution에 대한 평가 결과이다.
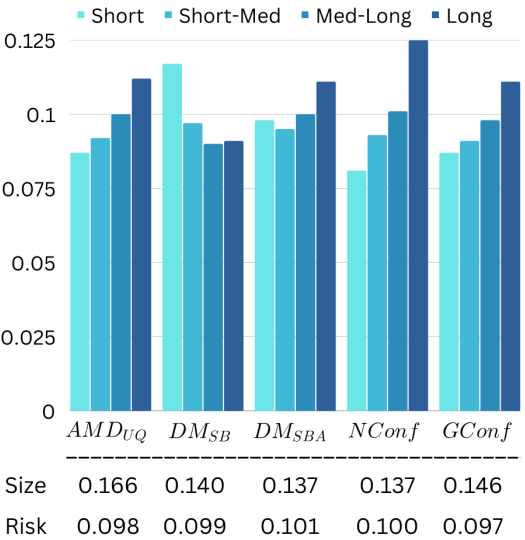
모든 모델이 RCPS 정의를 만족한다. 모든 모델이 $ADM_{UQ}$의 성능을 뛰어 넘었으며, $DM_{SBA}$와 N-Conffusion은 더 좁은 간격을 만들었다. $DM_{SBA}$의 size-stratified risk가 가장 좋았다.
다음은 N-Conffusion으로 추출한 bound들을 나타낸 것이다.

N-Conffusion이 유의미한 bound를 제공한다는 것을 알 수 있다. Error map을 보면 대부분의 error가 높은 주파수 영역에 있음을 알 수 있다.
2. Inpainting
다음은 inpainting에 대한 평가 결과이다.

모든 모델이 $ADM_{UQ}$의 성능을 뛰어 넘었다. N-Conffusion은 통제 위험에서 약간 벗어나지만 간격 크기 측면에서 뛰어나다.
다음은 다양한 방법을 inpainting task에 대하여 비교한 것이다.

$ADM_{UQ}$는 흐릿한 bound를 생성하지만 $DM_{SB}$는 가장 날카로운 간격을 생성하며 추정된 bound가 아티팩트를 포함할 수 있다. N-Conffusion은 사실적인 bound를 유지하면서 가장 좁은 간격을 구성한다.
다음은 N-Conffusion으로 추출한 bound들을 나타낸 것이다.

3. Is Diffusion Pretraining Necessary?
다음은 G-Conffusion과 동일한 finetuning 목적 함수로 ResNeXt와 ResNeSt를 사전 학습한 후 비교한 결과이다. ResNeXt는 Instagram 데이터셋에서 사전 학습되었고 ResNeSt는 ImageNet에서 사전 학습되었다.
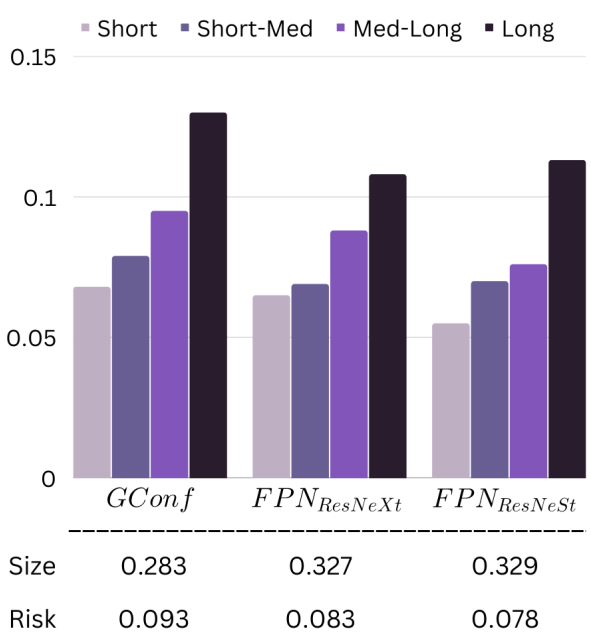
모든 방법이 risk-controlling 정의를 만족하지만, diffusion model로 사전 학습한 것이 생성한 간격이 가장 좁다.







![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)