Blogs

arXiv 2022. [Paper]
Justin Lovelace, Varsha Kishore, Chao Wan, Eliot Shekhtman, Kilian Weinberger
Cornell University
19 Dec 2022

Introduction

Diffusion model은 가우시안 분포에서 추출한 랜덤한 noise를 알 수 없는 데이터 분포의 샘플로 점진적으로 변환하는 방법을 학습하는 잠재 변수 모델이다. Diffusion model은 최근 이미지, 오디오, 비디오와 같은 연속적인 데이터 형시에 대하여 광범위한 성공을 거두었다. 또한 제어 가능한 생성과 state-of-the-art text-to-image 시스템에서도 큰 성공을 거두었다.

반면, 언어 생성 모델은 규모가 큰 autoregressive (AR) trasnformer가 주를 이루며, 몇몇 모델들은 다양한 언어 생성 task에서 인상적인 성능을 보였다. 이러한 모델에서 원하는 동작을 이끌어내는 것은 어렵고 종종 신중하고 즉각적인 엔지니어링이 필요하다.

제어 가능한 생성에 대한 diffusion model의 성공은 언어 생성 분야에 매력적이다. 그러나 지금까지는 불연속적인 상태에서 가우시안 noise로의 점진적인 전환이 이미지와 같은 연속 도메인에서만큼 자연스럽지 않았기 때문에 불연속적인 도메인에서는 제한적으로 사용되었다. 이전 연구들에서는 이산 데이터를 직접 모델링하려는 시도로 불연속적 상태 space에 대한 diffusion process를 정의했지만 이러한 접근 방식은 연속적인 diffusion model보다 뒤처졌다.

다른 연구에서는 연속적인 diffusion model을 단어 임베딩의 space에서 직접 학습시키고 반올림한 step으로 연속적인 생성을 디코딩하였다. 이런 연구들은 diffusion model을 AR 언어 모델의 잠재적인 대안으로서 제안하였다.

반대로, 본 논문은 diffusion model을 AR 생성의 대안이 아닌 필수 도구로 제안한다. 저자들은 연속적인 diffusion model이 사전 학습된 인코더-디코더 언어 모델의 latent space를 학습할 수 있다고 설명한다. Diffusion model에서 샘플링된 연속적인 벡터들은 사전 학습된 디코더를 사용하여 자연어로 디코딩될 수 있다. Diffusion model을 통해 불연속적인 분포를 직접 모델링하는 문제를 회피하고 자연어에 대한 연속적인 방법을 사용할 수 있다.

저자들은 latent diffusion model이 다양한 데이터셋에서 unconditional한 언어 생성과 conditional한 언어 생성 모두에 효과적임을 확인하였다. 특히, 본 논문의 접근 방식은 사전 학습된 GPT2 model보다 데이터 분포에서 새로운 텍스트를 생성하는 데에 효과적이라고 한다.

Methods

1. Latent Diffusion for Language

저자들은 denoising autoencoder로 사전 학습된 인코더-디코더 언어 모델인 BART의 latent space에서 latent diffusion model을 학습 시켰다. 일부 토큰이 마스킹된 발화가 주어지면 BART는 손상되지 않은 언어를 생성하도록 사전 학습된다. 기본적으로 인코더 layer와 디코더 layer가 6개, hidden size가 768인 BART-base를 사용한다. BART의 인코더와 디코더를 고정시키며, 프레임워크에서 denoising network $\hat{x}_\theta$만이 학습 가능한 파라미터를 가지고 있다.

Vocabulary $\mathcal{V}$에 대하여 $l$개의 one-hot vector들의 시퀀스로 표현되는 자연어 $w \in \mathbb{R}^{l \times \vert \mathcal{V} \vert}$가 주어지면, BART 인코더 $E$는 $w$를 어떤 연속적인 latent space로 매핑한다.

\[\begin{equation} x = E(w) \in \mathbb{R}^{l \times d} \end{equation}\]

그런 다음 BART 디코더 $D$가 근사적으로 원래 입력을 재구성한다.

\[\begin{equation} w \approx \tilde{w} = D(x) = D(E(w)) \in \mathbb{R}^{l' \times \vert \mathcal{V} \vert} \end{equation}\]

자연어 데이터셋 $\mathcal{D}$가 주어지면, 연속적인 diffusion model을 학습시키기 위해서는 연속적인 데이터를 샘플링하여야 한다.

\[\begin{equation} w \in \mathbb{R}^{l \times \vert \mathcal{V} \vert} \sim \mathcal{D} \end{equation}\]

이는 denoising network $\hat{x}_\theta (z_t, t)$가 $x$를 복구하도록 학습 가능해진다.

생성의 경우 잠재 변수 $z_T \in \mathbb{R}^{l \times d} \sim \mathcal{N}(0,I)$를 샘플링하여 BART latent space의 분포로 반복적으로 denoising해야 한다. 이미지의 diffusion은 고정된 해상도 $H \times W \times 3$에서 진행되므로 잠재 변수 $z_T \in \mathbb{R}^{H \times W \times 3}$을 샘플링하는 것이 적합하다.

반면, 언어는 길이가 다양하다. 데이터 $x \in \mathbb{R}^{l \times d}$의 경우 $l$은 데이터 샘플에 따라 다르다. 하지만 inference 시에는 $l_i$로 길이를 정해놓고 $z_T \in \mathbb{R}^{l_i \times d}$를 샘플링할 수 있다.

$l_i$를 선택하기 위하여 저자들은 데이터의 길이의 경험적 분포 $\mathcal{L}(\mathcal{D})$에서 $l_i$를 샘플링한다. 즉, 다음과 같이 둔다.

\[\begin{equation} \textrm{Pr} (l = l_i) = \frac{1}{\mathcal{D}} \sum_{w \in \mathcal{D}} \mathbb{1} \{ w \in \mathbb{R}^{l_i \times \vert \mathcal{V} \vert} \} \end{equation}\]

생성의 경우 먼저 $l_i \sim \mathcal{L}(\mathcal{D})$로 길이를 샘플링한 뒤 latent $z_T \in \mathbb{R}^{l_i \times d} \sim \mathcal{N}(0,I)$를 샘플링한다. 이는 표준 샘플링 알고리즘의 사용을 가능하게 한다.

2. Self-Conditioning

저자들은 샘플 품질을 개선한다고 알려진 self-conditioning 테크닉도 활용한다. Denoising network은 일반적으로 잠재 변수 $z_t$와 timestep $t$를 조건으로 받는다. Self-conditioning은 추가적으로 이전 timestep의 출력으로 신경망을 컨디셔닝하기 위하여 제안되었다.

\[\begin{equation} \tilde{x}_t = \hat{x}_\theta (z_t, t, \tilde{x}_{t+1}) \end{equation}\]

Inference 중에는 샘플링 과정이 본질적으로 반복적이고 $t$에서는 이미 이전 timestep의 출력 $\tilde{x}_{t+1}$을 계산하였기 때문에 신경망에 추가로 어떤 적용을 할 필요가 없다.

하지만 학습 과정에서는 denoising network가 추정 데이터를 활용하도록 수정해야 한다. 따라서 denoising network를 적용하기 전에 $T$에서의 inference를 정의해야 한다.

이전과 동일하게 각 학습 step에서 \(t \sim \mathcal{U} (\{1,\cdots,T\})\)를 샘플링한다. 확률 $p = 0.5$로 self-conditioning을 위한 어떠한 추정 데이터도 사용하지 않는다.

\[\begin{equation} \tilde{x}_{t, \emptyset} = \tilde{x}_\theta (z_t, t, \emptyset) \end{equation}\]

확률 $1 - p$로 먼저 \(\tilde{x}_{t, \emptyset}\)를 계산하여 inference를 따라한 뒤 다음과 같이 추가 추정을 계산한다.

\[\begin{equation} \tilde{x}_t = \tilde{x}_\theta (z_t, t, \textrm{sg}(\tilde{x}_{t, \emptyset})) \end{equation}\]

$\textrm{sg}()$는 stop-gradient 연산이다. 이 두 번째 추정은 loss를 계산하는 데 사용된다.

이 학습 과정은 self-conditioning이 없는 일반 inference도 가능하게 하며, 이는

\[\begin{equation} \tilde{x}_T = \tilde{x}_\theta (z_T, T, \emptyset) \end{equation}\]

을 샘플링하는 중에 첫 번째 추정치를 생성하는 데 사용된다. 나중 추정치는 self-conditioning은 다음과 같이 모두 계산할 수 있다.

\[\begin{equation} \tilde{x}_t = \hat{x}_\theta (z_t, t, \tilde{x}_{t+1}) \end{equation}\]

3. Class-Conditional diffusion

조건부 언어 생성을 위한 프레임워크의 능력을 평가하기 위하여 저자들은 이를 클래스 조건부 생성으로 확장한다. 저자들은 각 자연어 발화가 $C$개의 클래스 레이블 중 하나와 연결된 데이터셋을 사용한다고 가정한다. 클래스 레이블은 텍스트의 감정이나 텍스트의 주제 등을 표현한다. 따라서, 다음과 같은 데이터셋이다.

\[\begin{equation} (w, y) \in \mathcal{D}, \quad w \in \mathbb{R}^{l \times \vert \mathcal{V} \vert}, \quad y \in \{1, 2, \cdots, C\} \end{equation}\]

Denoising network를 클래스 레이블로 컨디셔닝하여 클래스 조건부 diffusion model을 학습시킨다. 클래스 레이블은 원래 데이터에 대한 정보를 전달하기 때문에 신경망은 denoising network를 guide하기 위해 추가 클래스 정보를 활용하는 방법을 학습한다. Self-conditioning과 같이 ground truth 클래스 레이블 $y_i$를 $p = 0.1$의 확률로 null 레이블 $y_\emptyset$으로 대체하며, 이를 통해 unconditional한 생성 능력도 유지한다.

Inference 시에는 클래스 $y$를 선택하여 샘플링 프로세스를 guide한다. 이전과 동일하게 $z_T \sim \mathcal{N}(0,I)$를 샘플링한 후 denoising network에 $y$에 해당하는 데이터를 생성하도록 한다.

\[\begin{equation} \tilde{x}_t = \hat{x}_\theta (z_t, t, y) \end{equation}\]

이를 통해 주어진 클래스에 대하여 텍스트를 생성한다.

본 논문의 접근 방식의 개요는 아래와 같다.

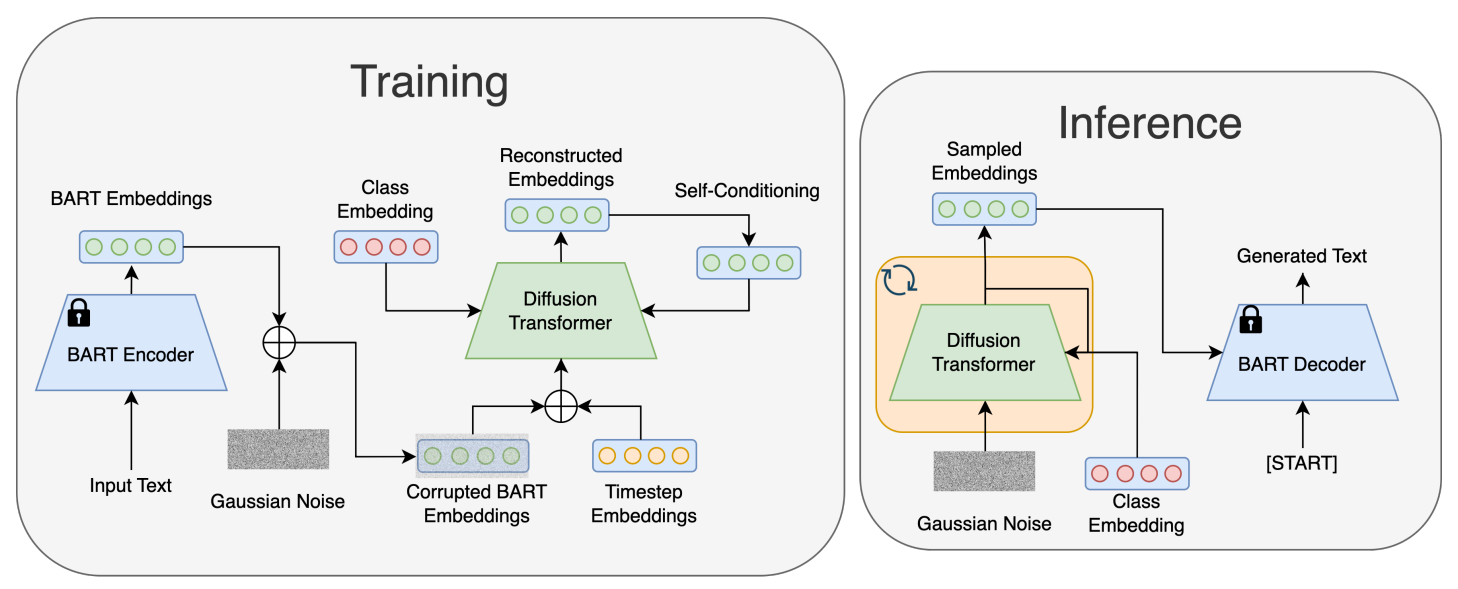
다음은 인코더-디코더 언어 모델, self-conditioning, 클래스 조건부 생성을 통합한 수정된 학습 알고리즘과 샘플링 알고리즘이다.

4. Denoising Network Architecture

Denoising network \(\tilde{x}_\theta (z_t, t)\)는 양방향 Pre-LN transformer이며, layer가 12개이고 hidden dimension $d_\textrm{tx}$가 768이다. 학습 가능한 absolute positional encoding, T5 relative positional biases, GeGLU 활성화 함수를 활용한다. $z_t$는 transformer의 입력 차원으로 project되며, transformer를 통과시킨 다음 LayerNorm과 linear layer로 처리되어 reconstruction을 얻는다.

이미지 diffusion과 비슷하게 yimestep 정보를 컨디셔닝한다. Timestep을 sinusoidal positional encoding $\psi (t) \in \mathbb{R}^{d_\textrm{tx}}$로 매핑하고 MLP를 통과시켜 time embedding $\textrm{MLP}(\psi (t)) \in \mathbb{R}^{d_\textrm{tx}}$를 얻는다.

이 time embedding을 입력 시퀀스애 더하고, 추가로 모든 feedforward layer의 출력 $h \in \mathbb{R}^{l \times d_\textrm{tx}}$에 adaptive layer normalization (AdaLN)을 적용한다.

\[\begin{equation} \textrm{AdaLN}(h,t) = t_s \odot \textrm{LayerNorm}(h) + t_b \\ (t_s, t_b) = \textrm{MLP}(\psi (t)) \in \mathbb{R}^{2 \times d_\textrm{tx}} \end{equation}\]

이는 이미지 diffusion model에 사용되는 AdaGN과 동일하게 구현된다.

Self-conditioning을 위하여 모든 self-attention layer와 feed-forward layer 사이의 cross-attention layer을 도입하며, 깨끗한 데이터의 이전 추정치에 대한 학습된 projection을 사용한다.

\[\begin{equation} \tilde{x}_{t+1} W + b \in \mathbb{R}^{l \times d_\textrm{tx}} \\ W \in \mathbb{R}^{d \times d_\textrm{tx}}, \quad b \in \mathbb{R}^{d_\textrm{tx}} \end{equation}\]

Prior 추정치 없이 denoising하기 위하여 학습 가능한 임베딩 $h_\emptyset \in \mathbb{R}^{d_\textrm{tx}}$을 사용한다.

클래스 레이블 \(y \in \{1,2,\cdots,C,\emptyset\}\)로 컨디셔닝하기 위하여 학습 가능한 클래스 임베딩 $C \in \mathbb{R}^{(C+1)\times d_\textrm{tx}}$를 도입한다. 클래스 임베딩을 self-conditioning 입력에 concat한다.

5. Implementation Details

이미지 diffusion model은 공통적으로 nosie 예측 모델 $\hat{\epsilon}\theta (z_t, t)$를 $\hat{x}\theta (z_t, t)$ 대신 사용한다.

\[\begin{equation} \hat{x}_\theta (z_t, t) = \frac{z_t - \sqrt{1 - \alpha_t} \hat{\epsilon}_\theta (Z_t, t)}{\sqrt{\alpha_t}} \end{equation}\]

저자들은 noise 예측 parameterization이 불안정하고 대신 denoising parameterization를 직접 활용한다는 것을 발견했다.

Latent space의 스케일을 조절하기 위해 latent space를 평균이 0이고 분산이 1이 되도록 정규화하고, 정규화된 latent space에서 diffusion model을 학습시킨다. 그런 다음 샘플링 후 디코딩 전에 정규화를 되돌린다. 첫 번째 학습 배치에서 정규화 통계를 계산한다.

저자들은 $T = 1000$으로 모델을 학습시켰으며, DDPM에서 도입된 linear schedule을 사용한다. DDIM과 같이 inference 중에는 샘플링 step을 250으로 줄여 생성을 가속화한다. 샘플링된 latent vector들을 디코딩할 때에는 beam size가 4이고 repetition penalty가 1.2인 beam search를 활용하여 중복되는 trigram의 생성을 방지한다.

Experiments

• 데이터셋: E2E, ROCStories, Standford Sentiment Treebank, AG News Topic Classification
• 평가 지표: MAUVE Score, Perplexity (Ppl), Unique Tokens (Uniq), Diversity (Div), Memorization (Mem)
  • 모든 실험에서 1000개를 샘플링
  • MAUVE 점수의 경우 1000개씩 5번을 뽑아 5번의 평균과 표준편차를 구함

1. Unconditional Diffusion

저자들은 E2E와 ROCStories 데이터셋으로 unconditional diffusion model을 학습하였다. 언어 생성에 대한 평가 지표는 아래 표와 같다.

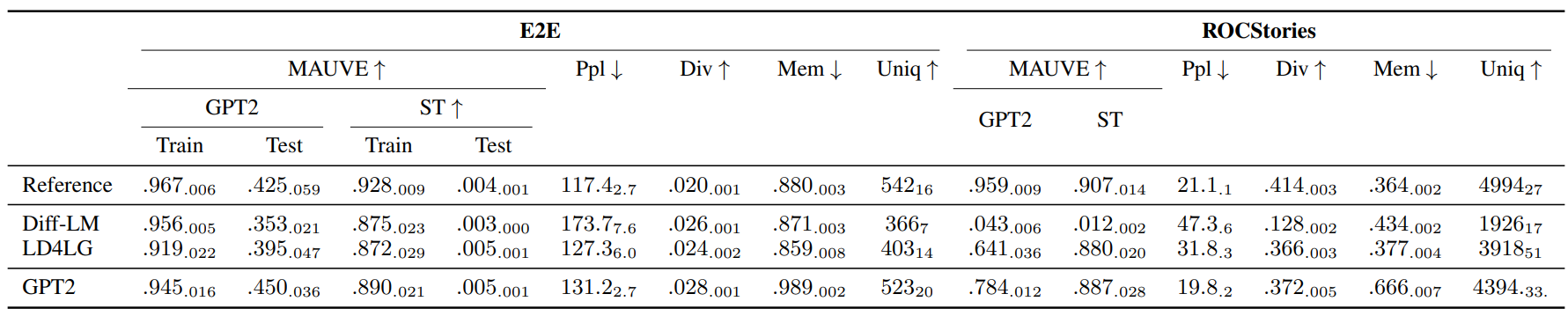
다음은 ROCStories에서 MAUVE 점수와 memorization 사이의 trade-off를 나타낸 것이다. 더 어두운 점이 학습 후반에 발생한 것이다.

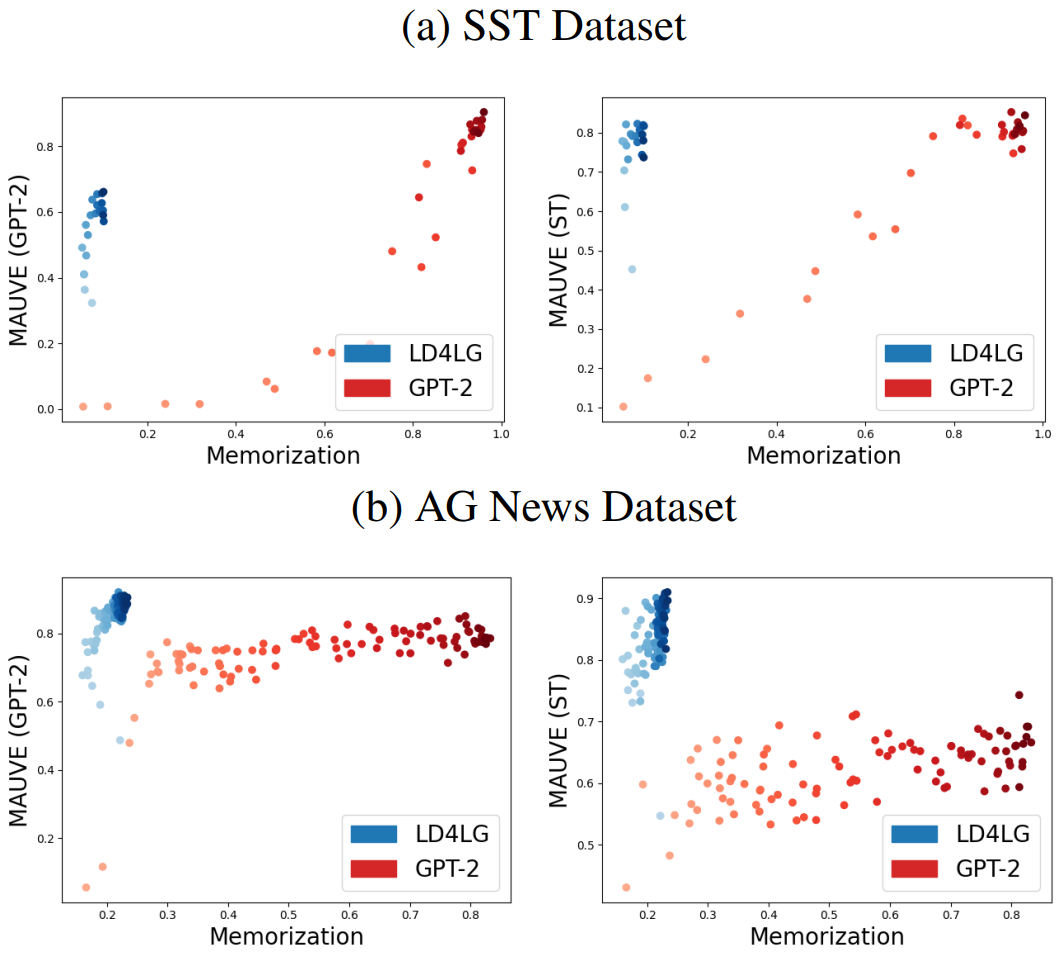
2. Class-Conditional Diffusion

Class-conditional diffusion model은 SST와 AG News 데이터셋에서 학습되었다. 다음은 두 데이터셋에서 MAUVE 점수와 memorization 사이의 trade-off를 나타낸 것이다.

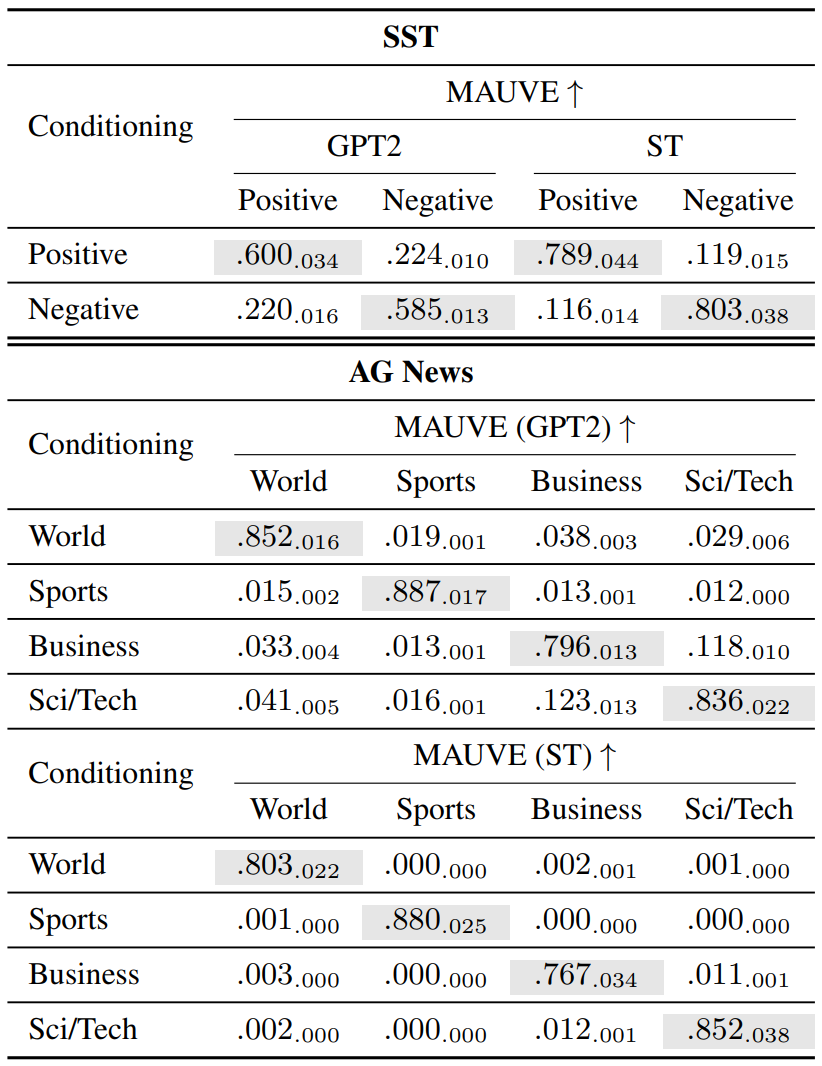
Class-conditional diffusion model의 언어 생성에 대한 평가 지표는 아래 표와 같다.

다음 표는 class-conditional 생성에 대한 평가 지표를 나타낸 것이다.

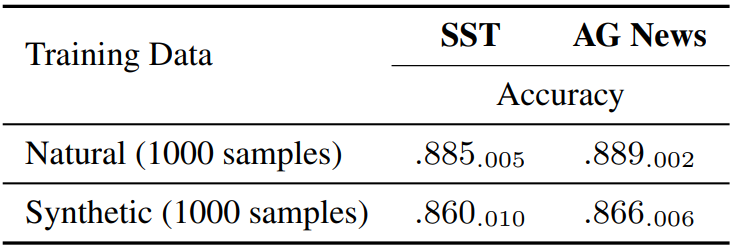
저자들은 클래스가 고르게 분포되도록 1000개의 샘플을 생성한 다음 classifier를 학습시키고 성능을 평가하였다. 다음은 DeBERTa-v3-base를 finetuning한 모델에 대한 classifier 성능이다.

4. Ablation Studies

다음은 self-conditioning의 영향에 대한 ablation study 결과이다.

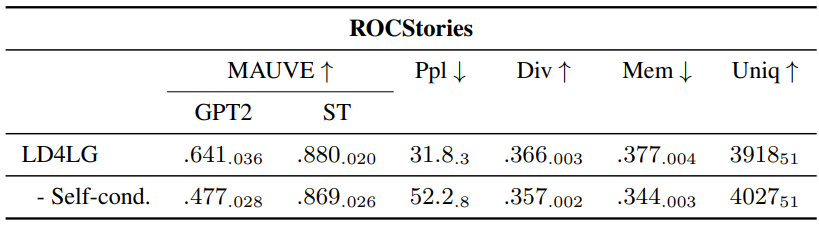
Self-conditioning이 생성된 텍스트의 MAUVE 점수와 perplexity를 상당히 개선시지만 memorization은 조금만 증가하였다.