Blogs

CVPR 2022. [Paper] [Page] [Github]
Konpat Preechakul, Nattanat Chatthee, Suttisak Wizadwongsa, Supasorn Suwajanakorn
VISTEC, Thailand
30 Dec 2021

Introduction

Diffusion 기반의 생성 모델 (DPM)과 score 기반의 생성 모델은 최근 사실적이고 고품질의 이미지를 합성하는 데 성공하였다. 두 모델은 긴밀힌 연관되어 있어 비슷한 목적 함수를 최적화한다. 최근 연구들은 이론적인 측면과 실용적인 측면 모두에서 DPM을 개선시켰다. 한편 본 논문에서는 DPM이 좋은 표현 학습자인 지 질문을 던진다. 특히, 저자들은 높은 수준의 의미를 포함하면서도 이미지를 거의 정확하게 재구성할 수 있는 의미 있고 디코딩 가능한 이미지 표현을 추출하려고 한다. 저자들은 diffusion model에 중점을 두지만 score 기반 모델에도 적용할 수 있다.

표현을 학습하는 한 가지 방법은 autoencoder를 통과시키는 것이다. 생성 프로세스를 거꾸로 실행하여 입력 이미지 $x_0$를 공간적 잠재 변수 $x_T$로 변환하는 encoder-decoder 역할을 할 수 있는 특정 종류의 DPM이 있다. 그러나 결과 잠재 변수에는 높은 수준의 의미가 부족하며, disentanglement, 압축, 잠재 공간에서 유의미힌 선형 보간과 같은 기타 속성이 부족하다. 또다른 방법은 GAN을 학습시키고 GAN inversion을 사용하여 표현을 추출하는 것이다. 결과 code가 풍부한 의미를 포함하지만 이 방법은 입력 이미지를 충실하게 재구성하는 데 어려움을 겪는다. 이러한 문제를 극복하기 위해 디코딩 가능한 표현 학습을 위해 강력한 DPM을 활용하는 diffusion 기반의 autoencoder를 제안한다.

디코딩 가능한 유의미한 표현을 찾는 것은 높은 레벨의 의미와 낮은 레벨의 stochastic variation을 모두 포착할 수 있어야 한다. 본 논문의 주요 아이디어는 학습 가능한 encoder로 높은 수준의 의미를 찾고 DPM으로 stochastic variation을 디코딩하고 모델링하여 두 레벨의 표현을 모두 학습하는 것이다. 구체적으로 DDIM의 conditional한 버전을 decoder로 사용하고 latent code를 2개의 subcode로 나눈다.

“Semantic” subcode는 CNN encoder로 추론되며 “stochastic” subcode는 semantic subcode로 컨디셔닝된 DDIM의 reverse process로 추론된다. 다른 DPM들과 달리 DDIM은 DPM의 목적 함수를 보존하면서 forward process를 non-Markovian으로 수정한다. 이 수정은 결정론적으로 초기 noise에 대응하는 이미지를 인코딩하며, stochastic subcode가 초기 noise다.

이 프레임워크가 가지는 의미는 두 가지이다.

1. Target output의 의미 정보로 DDIM을 컨디셔닝하면 denoising이 쉽고 빨라진다.
2. 생성된 표현은 선형적이고 의미론적으로 유의미하며 디코딩 가능하다.

이 중요한 속성은 GAN 기반의 방법들이 굉장히 어려워하는 다양한 task에서 DPM을 활용할 수 있게 한다. 실제 이미지에서 작동하기 전에 오류에 취약한 inversion에 의존하는 GAN과 달리, 본 논문의 방법은 입력을 인코딩하기 위해 최적화가 필요하지 않으며 원본의 디테일이 보존된 고품질 출력을 생성한다.

일반적으로 unconditional한 생성을 위해 설계되지 않은 autoencoder임에도 불구하고 본 논문의 프레임워크는 다른 DPM을 semantic subcode 분포에 맞춰 이미지 샘플을 생성하는 데 사용할 수 있다. 이 조합은 일반 DPM에 비해 unconditional한 생성에서 경쟁력 있는 FID를 얻는다. 또한, 작고 유의미한 잠재 공간에서 샘플링할 수 있으므로 few-shot으로 conditional한 생성이 가능하다. Few-shot을 위한 다른 DPM 기반 테크닉과 비교할 때, 본 논문의 방법은 추가 contrastive learning 없이 소수의 레이블된 예제만으로 설득력 있는 결과를 생성한다.

Diffusion autoencoders

유의미한 latent code를 추구하기 위해 추가 잠재 변수 $z_\textrm{sem}$을 조건으로 하는 조건부 DDIM 이미지 decoder $p(x_{t−1} \vert x_t, z_\textrm{sem})$와 이미지 $x_0$에서 $z_\textrm{sem}$으로의 매핑을 학습하는 semantic encoder \(z_\textrm{sem} = \textrm{Enc}_\phi (x_0)\)를 설계한다. 여기서 조건부 DDIM decoder는 잠재 변수 $z = (z_\textrm{sem}, x_T)$를 입력으로 한다. $z$는 상위 레벨의 “semantic” subcode $z_\textrm{sem}$과 하위 레벨의 “stochastic” subcode $x_T$로 구성된다. 프레임워크에서 DDIM은 decoder와 stochastic encoder 역할을 모두 수행한다.

Diffusion autoencoder는 다음 그림과 같이 구성된다.

2D latent map과 같은 공간적 조건부 변수를 사용하는 다른 조건부 DPM과 다르게, $z_\textrm{sem}$은 차원이 $d = 512$인 비공간적 벡터로 특정 영역에 대한 의미가 아닌 전역적인 의미를 인코딩한다. 본 논문의 목표 중 하나는 의미론적으로 풍부한 잠재 공간을 학습하여 재구성 능력을 유지하면서 interpolation을 부드럽게 하는 것이다.

1. Diffusion-based Decoder

조건부 DDIM decoder는 $z = (z_\textrm{sem}, x_T)$를 입력을 받아 이미지를 생성한다. 이 decoder는 $q(x_{t-1} \vert x_t, x_0)$에 일치하도록 $p_\theta (x_{t-1} \vert x_t, z_\textrm{sem})$을 모델링하는 조건부 DDIM으로, 다음의 reverse process를 따른다.

\[\begin{aligned} p_\theta (x_{0:T} \vert z_\textrm{sem}) &= p(x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t, z_\textrm{sem}) \\ p_\theta (x_{t-1} \vert x_t, z_\textrm{sem}) &= \begin{cases} \mathcal{N} (f_\theta (x_1, 1, z_\textrm{sem}), 0) & \textrm{if} \; t = 1 \\ q (x_{t-1} \vert x_t, f_\theta (x_t, t, z_\textrm{sem})) & \textrm{otherwise} \end{cases} \end{aligned}\]

DDIM과 마찬가지로 위 식의 $f_\theta$를 noise 예측 신경망 $\epsilon_\theta (x_t, t, z_\textrm{sem})$으로 parameterize할 수 있다.

\[\begin{equation} f_\theta (x_t, t, z_\textrm{sem}) = \frac{1}{\sqrt{\alpha_t}} (x_t - \sqrt{1 - \alpha_t} \epsilon_\theta (x_t, t, z_\textrm{sem})) \end{equation}\]

이 신경망은 UNet의 수정된 버전이다. 학습은 $L_\textrm{simple}$ 손실 함수를 최적화하여 진행된다.

\[\begin{equation} L_\textrm{simple} = \sum_{t=1}^T \mathbb{E}_{x_0, \epsilon_t} \bigg[ \| \epsilon_\theta (x_t, t, z_\textrm{sem}) - \epsilon_t \|_2^2 \bigg] \\ \epsilon_t \in \mathbb{R}^{3 \times h \times w} \sim \mathcal{N} (0,I), \quad x_t = \sqrt{\alpha_t} x_0 + \sqrt{1 - \alpha_t} \epsilon_t \end{equation}\]

여기서 $T$는 1000과 같은 큰 숫자로 설정된다. 이 간단한 손실 함수는 DDPM과 DDIM 모두에서 최적화에 사용되었으며 실제 variational lower bound가 아니다. 학습 중에는 stochastic subcode $x_T$가 필요하지 않다. 저자들은 AdaGN (adaptive group normalization layer)을 사용하여 $t$와 $z_\textrm{sem}$으로 컨디셔닝된 UNet을 사용한다.

\[\begin{equation} \textrm{AdaGN} (h, t, z_\textrm{sem}) = z_s (t_s \textrm{GroupNorm}(h) + t_b) \end{equation}\]

여기서 $z_s \in \mathbb{R}^c = \textrm{Affine}(z_\textrm{sem})$이고 $(t_s, t_b) \in \mathbb{R}^{2 \times c} = \textrm{MLP} (\psi (t))$는 sinusoidal encoding function $\psi$와 MLP로 구성된다.

2. Semantic encoder

Semantic encoder $\textrm{Enc}(x_0)$의 목표는 입력 이미지를 $z_\textrm{sem} = \textrm{Enc}(x_0)$로 요약하는 것이며, $z_\textrm{sem}$은 decoder가 denoise하고 출력 이미지를 예측하는 것을 돕기 위해 필요한 정보이다. 저자들은 어떠한 아키텍처도 encoder로 가정하지 않았지만, 실험에서는 UNet decoder의 앞의 절반과 동일한 아키텍처로 이루어져 있다. 정보가 풍부한 $z_\textrm{sem}$으로 DDIM을 컨디셔닝하면 더 효율적인 denoising process가 된다는 장점이 있다.

3. Stochastic encoder

조건부 DDIM은 입력 이미지 $x_0$를 stochastic subcode $x_T$로 인코딩하는 데도 사용되며, 다음과 같이 결정론적인 생성 프로세스를 반대로 실행하여 인코딩한다.

\[\begin{equation} x_{t+1} = \sqrt{\vphantom{1} \alpha_{t+1}} f_\theta (x_t, t, z_\textrm{sem}) + \sqrt{1 - \alpha_{t+1}} \epsilon_\theta (x_t, t, z_\textrm{sem}) \end{equation}\]

이 프로세스를 stochastic encoder로 생각할 수 있으며, 이는 $x_T$가 $z_\textrm{sem}$에 남은 정보만을 인코딩하도록 만들기 때문이다. $z_\textrm{sem}$은 stochastic한 디테일을 압축하는 데 제한된 용량을 가지고 있다. Semantic encoder와 stochastic encoder를 모두 활용하여 autoencoder는 입력 이미지를 마지막 디테일까지 포착하는 동시에 하위 task에 대한 높은 수준의 표현 $z_\textrm{sem}$을 제공할 수 있다.

앞서 말했지만 stochastic encoder는 학습 중에 사용하지 않으며, 정확한 reconstruction이나 inversion에 필요한 $x_T$를 계산하는 데에만 사용된다.

Sampling with diffusion autoencoders

Decoder를 $z_\textrm{sem}$으로 컨디셔닝하기 때문에 diffusion autoencoder는 더 이상 생성 모델이 아니다. 따라서 autoencoder에서 샘플링하기 위해서는 latent 분포에서 $z_\textrm{sem} \in \mathbb{R}^d$를 샘플링하는 추가 메커니즘이 필요하다.

VAE가 이 task에서는 매력적인 선택지이지만, latent code의 풍부한 정보를 유지하는 것과 VAE의 샘플 품질을 유지하는 것 사이의 균형을 맞추는 것이 어렵다. 또다른 선택지로는 GAN이 있지만, GAN은 DPM의 주요 강점 중 하나인 학습 안정성이 복잡하게 만든다. 따라서 저자들은 latent DDIM이라 부르는 또다른 DDIM $p_w (z_{\textrm{sem}, t-1} \vert z_{\textrm{sem},t})$를 사용한다.

Latent DDIM으 학습은 $L_\textrm{latent}$를 최적화하여 진행된다.

\[\begin{equation} L_\textrm{latent} = \sum_{t=1}^T \mathbb{E}_{z_\textrm{sem}, \epsilon_t} \bigg[ \| \epsilon_w (z_{\textrm{sem},t}, t) - \epsilon_t \|_1 \bigg], \\ z_{\textrm{sem}, t} = \sqrt{\vphantom{1} \alpha_t} z_\textrm{sem} + \sqrt{1 - \alpha_t} \epsilon_t, \quad \epsilon_t \in \mathbb{R}^d \sim \mathcal{N}(0,I) \end{equation}\]

경험적으로 $L_1$ loss가 $L_2$ loss보다 더 잘 작동한다고 한다. 1D나 2D가 아닌 비공간적 데이터를 위해 설계된 아키텍처가 없으므로 10~20개의 layer로 이루어진 MLP에 skip connection을 적절히 사용하여 아키텍처를 구성하였다고 한다.

학습 시에는 먼저 semantic encoder ($\phi$)와 이미지 decoder ($\theta$)를 수렴할 때가지 먼저 학습하고 그 다음에 latent DDIM ($w$)를 semantic encoder를 고정시켜 놓고 학습한다. Latent DDIM은 학습 시작 전에 표준 정규 분포로 초기화된다. Diffusion autoencoder의 unconditional한 샘플링은 다음 순서로 진행된다.

1. Latent DDIM으로 $z_\textrm{sem}$을 생성
2. $z_\textrm{sem}$을 unnormalize
3. $x_T \sim \mathcal{N}(0,I)$를 샘플링
4. Decoder를 사용하여 $z = (z_\textrm{sem}, x_T)$를 디코딩

Latent DDIM을 나중에 학습하는 데는 몇 가지 경험적인 이유가 있다. 먼저, latent DDIM을 학습시키는 것이 전체 학습 시간 중 작은 부분만을 차지하기 때문에 나중에 학습하면 같은 diffusion autoencoder에서 다양한 latent DDIM들을 실험해 볼 수 있다. 또다른 이유는 어떠한 제약을 두지 않음으로써 $z_\textrm{sem}$을 최대한 표현력 있게 유지하여 잠재 변수의 품질을 타협할 수 있게 된다.

Experiments

1. Latent code captures both high-level semantics and low-level stochastic variations

높은 레벨의 의미들은 대부분 $z_\textrm{sem}$에서 포착되고 $x_T$에서는 아주 조금만 포착된다는 것을 설명하기 위하여, 저자들은 먼저 $x_0$에서 $z_\textrm{sem} = \textrm{Enc}(x_0)$를 계산하고 $x_T^i \sim \mathcal{N}(0,I)$를 여러 번 샘플링하여 $z^i = (z_\textrm{sem}, x_T^i)$를 디코딩해 보았다.

다음 그림은 주어진 $z_\textrm{sem}$에 다양한 $x_T$를 더하여 디코딩한 결과이다.

위 결과를 보면 stochastic subcode $x_T$가 사소한 디테일에만 영향을 주며 전체적인 외형은 그대로인 것을 확인할 수 있다. $z_\textrm{sem}$에 변화를 주면 완전히 다른 얼굴 모양의 사람 이미지를 얻을 수 있다.

Semantically meaningful latent interpolation

유용한 latent space의 바람직한 속성 중 하나는 latent space에서의 간단한 선형 변화로 이미지의 의미론적 변화를 표현할 수 있다는 것이다. 다음 그림은 다양한 방법으로 진행한 interpolation의 결과를 보여준다.

$z_\textrm{sem}$은 linear interpolation (Lerp)으로 interpolation을 하였고 $x_T$는 spherical linear interpolation (Slerp)로 interpolation을 하였다.

3. Attribute manipulation on real images

Latent space에서 이미지 semantic과 linear motion 또는 separability 사이의 관계를 평가하는 또다른 방법은 $z_\textrm{sem}$을 특정 방향으로 움직여 이미지의 변화를 보는 것이다. 미소와 같은 타겟 속성의 부정 이미지와 긍정 이미지의 latent code에 대해 학습된 linear classifier의 가중치 벡터에서 이러한 방향을 찾음으로써 이 task는 결과적으로 이미지의 semantic 속성을 변경한다. 이 task를 위한 전문적인 테크닉이 존재하지만, 저자들은 가장 간단한 선형 연산을 사용하여 품질과 latent space의 적용 가능성을 보이고자 했다.

다음은 CelebA-HQ의 이미지와 속성 레이블을 사용하여 linear classifier를 학습시키고 CelebA-HQ와 FFHQ에서 테스트한 결과이다.

본 논문의 autoencoder는 FFHQ로 학습하였지만 finetuning 없이 CelebA-HQ에도 잘 일반화된다. 본 논문의 방법은 국소적인 feature (ex. 미소)를 바꾸면서 나머지 이미지와 디테일을 굉장히 잘 유지하였다. 전역적인 속성 (ex. 나이)의 경우 다양한 feature들을 동시에 바꿔야하며, 굉장히 그럴듯하고 사실적인 결과가 나왔다.

추가로 linear classifier의 정확도를 비교하였을 때 AUROC (클수록 좋음)가 본 논문의 방법은 0.925이고 StyleGAN-$\mathcal{W}$는 0.891이었다.

GAN 기반의 조작 테크닉과 다르게 diffusion autoencoder의 새로운 장점은 조작에 무관하게 디테일을 보존하면서 실제 이미지를 조작할 수 있다는 것이다. GAN의 경우 실제 이미지가 충실히 GAN의 latent space로 invert되지 않기 때문에 디테일들이 다르게 대체된다. 최근 나온 score 기반 조작 테크닉인 SDEdit과 비교하였을 때 본 논문의 방법은 latent code를 간단히 수정하여 semantic 속성을 바꿀 수 있다는 장점이 있다.

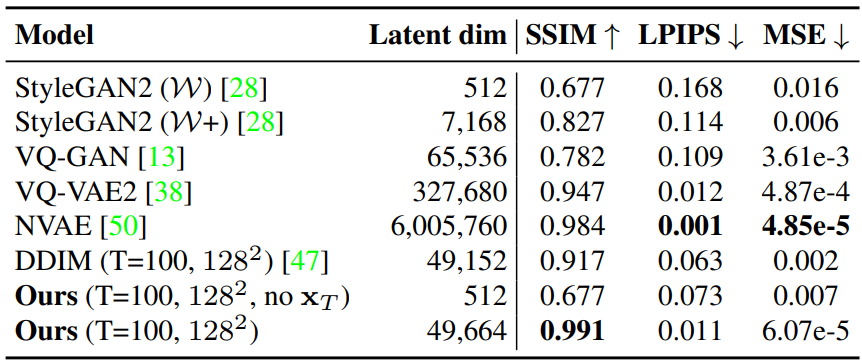
4. Autoencoding reconstruction quality

Autoencoder의 좋은 reconstruction 품질이 반드시 좋은 표현 학습의 지표는 아닐 수 있지만 이 속성은 정확한 encoding-decoding 능력이 필요한 압축이나 이미지 조작과 같은 많은 응용에서 중요한 역할을 한다. 이러한 task들에서 MSE나 $L_1$ 손실 함수에 의존하는 전통적인 autoencoder는 성능이 좋지 않고 흐릿한 결과를 생성한다.

발전된 autoencoder들은 perceptual loss와 adversarial loss를 추가하거나 잠재 변수들의 계층에 의존한다. Diffusion autoencoder는 유의미하고 간결한 semantic subcode로 이루어진 합리적인 크기의 latent code를 생성하는 새로운 디자인이며, state-of-the-art autoencoder들과 비교하였을 때 경쟁력 있다. 핵심은 덜 압축 가능한 확률적인 디테일들의 재구성을 조건부 DDIM에 위임하는 2단계 인코딩이다.

다음 표는 다양한 모델들의 reconstruction 품질을 평가한 것이다.

추가로, 저자들은 다음 2가지에 대한 ablation study를 진행하였다.

1. $z_\textrm{sem}$만 인코딩되고 $x_T$는 $\mathcal{N}(0,I)$에서 샘플링할 때의 reconstruction 품질
2. $z_\textrm{sem}$의 차원을 64에서 512까지 변경한 후 4800만 개의 이미지로 autoencoder를 학습할 때

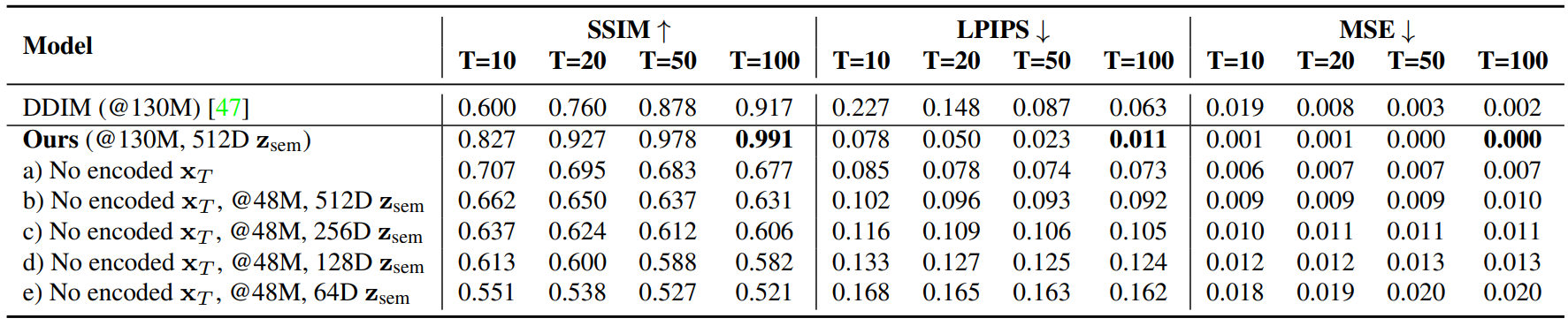
모든 경우 사실적인 결과를 생성하지만 latent 차원이 높을수록 fidelity가 좋아진다.

5. Faster denoising process

$z_\textrm{sem}$으로 denoising process를 컨디셔닝할 때의 이점 중 하나는 생성이 빨라진다는 것이다. DPM들이 생성에 많은 step이 필요한 주된 이유는 가우시안 분포만을 사용하여 $p(x_{t-1} \vert x_t)$를 근사하기 때문이다.

최근에는 더 나은 샘플링 간격이나 noise schedule을 찾거나 효율적인 solver로 score 기반 ODE를 풀어 샘플링 속도를 개선하려는 시도들이 있었다. Diffusion autoencoder는 이 문제를 직접 해결하는 것을 목표로 하지 않으며 타겟 샘플에 대한 접근이 부족한 생성 모델과 같은 맥락에서 비교할 수도 없다. 그러나 DPM 프레임워크 내에서 미치는 영향을 언급할 가치가 있다.

Denoising network에 $x_0$가 알려진 경우를 고려해보자. Noise 예측 task는 사소해지며 $q(x_{t-1} \vert x_t, x_0)$는 timestep의 수와 무관하게 가우시안 분포이다. Diffusion autoencoder가 $p(x_{t-1} \vert x_t, z_\textrm{sem})$을 모델링하므로 $z_\textrm{sem}$이 $x_0$의 많은 정보를 포착한 경우 $p(x_{t-1} \vert x_t, z_\textrm{sem})$이 $p(x_{t-1} \vert x_t)$보다 $q(x_{t-1} \vert x_t, x_0)$에 대한 더 좋은 근사이다.

다음 그림은 diffusion autoencoder가 DDIM 보다 더 적은 step으로 $x_0$를 더 정확하게 예측하는 것을 보여준다.

6. Class-conditional sampling

본 논문의 프레임워크는 few-shot 조건부 생성에도 사용할 수 있다. 다음 표는 본 논문의 방법이 어떠한 self-supervised contrastive learning을 사용하지 않고 D2C와 비교할만한 FID를 달성한 것을 보여준다.

Binary classifier는 50개의 positive와 negative로 학습되었으며 Positive-unlabeled (PU) classifier는 100개의 positive와 레이블이 없는 10000개의 이미지로 학습되었다.

7. Unconditional sampling

Unconditional한 샘플들의 품질을 평가하기 위하여 $z_\textrm{sem}$을 먼저 latent DDIM으로 샘플링한 뒤 decoder로 $z = (z_\textrm{sem}, x_T \sim \mathcal{N}(0,I))$를 디코딩한다.

Diffusion autoencoder는 모든 timestep 수에 대하여 DDIM보다 더 좋은 FID를 기록하였다. “+ autoencoding”은 테스트 이미지로부터 인코딩된 ground-truth 잠재 변수로 diffusion autoencoder를 학습시킨 reference이다.