Blogs

arXiv 2020. [Paper] [Github]
Karlis Freivalds, Sergejs Kozlovics
13 Nov 2020

Introduction

손글씨 데이터는 온라인 포맷과 오프라인 포맷으로 저장될 수 있다. 온라인 데이터는 일련의 펜의 stroke로 렌더링되며 오프라인 데이터는 이미지로 저장된다. 대부분의 온라인 손글씨 생성은 RNN 기반이며 대부분의 오프라인 손글씨 생성은 GAN 기반이다. 두 방법 모두 사실적이고 다양한 손글씨를 생성한다.

Diffusion probabilistic model (DPM)은 Markov chain으로 가우시안 같이 알고있는 분포에서 더 복잡한 데이터 분포로 변환한다. Diffusion process는 데이터 분포에 점진적으로 가우시안 noise를 더하여 간단한 분포로 변환하며, 생성 모델은 이 diffusion process를 reverse하도록 학습된다.

본 논문에서는 온라인 손글씨 생성을 위한 DPM을 제안하며, autogressive와 GAN 기반의 손글씨 생성의 장점을 모두 갖고 있다. 본 논문의 모델은 온라인 데이터의 글씨 스타일 feature를 통합하여 온라인 포맷으로 샘플을 생성할 수 있다. 또한 어떠한 텍스트, 스타일, adversarial 기반의 손실 함수도 필요하지 않으며 간단한 학습과 샘플링 과정으로 사실적인 손글씨 샘플을 원본과 비슷한 스타일로 생성할 수 있다.

Diffusion Models for Handwriting Generation

1. Diffusion Probabilistic Models

$q(y_0)$를 데이터 분포라 하고, $y_1, \cdots, y_T$를 $y_0$와 같은 차원의 잠재 변수라 하자. Diffusion model은 noise를 추가하는 diffusion process와 noise를 제거하는 reverse process로 구성된다. Diffusion process는 고정된 noise schedule $\beta_1, \cdots, \beta_T$를 기반으로 각 iteration에서 가우시안 noise를 추가하는 고정된 Markov chain으로 정의된다.

\[\begin{equation} q (y_{1:T} \vert y_0) = \prod_{t=1}^T q(y_t \vert y_{t-1}), \quad \quad q(y_t \vert y_{t-1}) = \mathcal{N}(y_t; \sqrt{1-\beta_t}y_{t-1}, \beta_t I) \end{equation}\]

Reverse process는 $\theta$로 parameterize된 Markov chain으로 정의된다.

\[\begin{equation} p(y_T) = \mathcal{N}(y_T; 0, I), \quad \quad p_\theta (y_{0:T}) = p(y_T) \prod_{t=1}^T p_\theta (y_t \vert y_{t-1}) \end{equation}\]

여기서 $p_\theta (y_{t-1} \vert y_t)$는 noise를 추가하는 $q(y_t \vert y_{t-1})$의 효과를 reverse하도록 학습된다.

\[\begin{equation} p_\theta (y_{t-1} \vert y_t) = \mathcal{N} (y_{t-1}; \mu_\theta (y_t, t), \Sigma_\theta (y_t, t)) \end{equation}\]

여기서 $\Sigma_\theta (y_t, t) = \sigma_t^2 I$이고 $\sigma_t^2$는 $\beta_t$에 관련된 상수이다. Forward process posterior는 다음과 같이 정의된다.

\[\begin{equation} q(y_{t-1} | y_t, y_0) = \mathcal{N} (y_{t-1}; \tilde{\mu} (y_t, y_0), \sigma_t^2 I) \end{equation}\]

몇몇 상수를 정의하면 $y_t$는 임의의 step $t$에 대하여 closed form으로 계산할 수 있다.

\[\begin{equation} \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{s=1}^t \alpha_s, \quad \epsilon \sim \mathcal{N} (0, I), \quad y_t = \sqrt{\vphantom{1} \bar{\alpha}_t} y_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]

Timestep $t - 1$에서의 손실 함수는 다음과 같다.

\[\begin{equation} L_{t-1} = \mathbb{E}_{y_0, \epsilon} \bigg( \frac{1}{2\sigma^2} \bigg\| \frac{1}{\sqrt{\alpha}_t} \bigg(y_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon \bigg) - \mu_\theta (y_t, t) \bigg\|^2 \bigg) \end{equation}\]

DDPM 논문에서는 score 기반 생성 모델과 유사하도록 DPM을 reparameterize하며 diffusion model $\epsilon_\theta$는 $\epsilon$를 예측한다. 손실 함수는 다음과 같다.

\[\begin{equation} L_{t-1} = \mathbb{E}_{t, \epsilon} [C_t \| \epsilon - \epsilon_\theta (y_t, t) \|_2^2], \quad C_t = \frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1- \bar{\alpha}_t)} \end{equation}\]

샘플링 단계에서 $y_{t-1}$을 샘플링하여 diffusion process에서 더해진 noise를 점진적으로 제거한다.

\[\begin{equation} y_{t-1} = \frac{1}{\sqrt{\alpha_t}} \bigg( y_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (y_t, t) \bigg) + \sigma_t z, \quad z \sim \mathcal{N} (0, I) \end{equation}\]

저자들은 실험에서 기존의 샘플링 과정을 수정하면 이점이 있다는 것을 발견하였다. 먼저 모델이 $\epsilon$을 예측하면 이를 이용하여 $y_0$를 근사한다.

\[\begin{equation} y_0 \approx \hat{y}_0 = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_t}} (y_t - \sqrt{1- \bar{\alpha}_t} \epsilon_\theta (y_t, t)) \end{equation}\]

$y_0$의 근사값으로 $y_{t-1}$을 계산한다.

\[\begin{equation} y_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \hat{y}_0 + \sqrt{1 - \bar{\alpha}_{t-1}} z, \quad z \sim \mathcal{N} (0, I) \end{equation}\]

두 식을 결합하면 다음과 같다.

\[\begin{equation} y_{t-1} = \frac{1}{\sqrt{\alpha_t}} (y_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_\theta (y_t, t)) + \sqrt{1 - \bar{\alpha}_{t-1}} z, \quad z \sim \mathcal{N} (0, I) \end{equation}\]

2. Conditional Handwriting Generation

각 데이터 포인트 $x_0$는 $N$개의 벡터 $x_1, \cdots, x_N$으로 이루어져 있다. 각 벡터 \(x_n \in \mathbb{R}^2 \times \{0,1\}\)은 이전 stroke에서 $x$와 $y$방향으로 펜이 이동한 위치로 이루어져 있다. 또한 binary entry는 펜이 stroke를 쓸 때 0, 아닐 때 1을 나타낸다. 각 손글씨 시퀀스는 글을 쓴 사람의 스타일 정보 $s$가 포함된 오프라인 이미지와 관련 있다.

여기에는 한 가지 기술적 문제가 있다. 앞서 말한 reverse process는 가우시안 분포로 parameterize된다. 하지만 binary entry는 가우시안 분포로 parameterize할 수 없다. 따라서 가우시안 분포 대신에 베르누이 분포로 parameterize하며, 이 또한 closed form으로 계산할 수 있다.

따라서 각 데이터 포인트 $x_0$를 stroke를 나타내는 $y_0$와 stroke가 그려졌는 지를 나타내는 $d_0$로 나누어야 한다. 각 step $t$에서 모델 \(d_\theta (y_t, c, s, \sqrt{\vphantom{1} \bar{\alpha}_t})\)는 stroke가 그려졌는지 \(\hat{d}_0\)를 추정한다. $d_\theta$는 $\epsilon_\theta$와 모든 파라미터를 공유하며, stroke loss와 pen-draw loss는 다음과 같다.

\[\begin{equation} L_\textrm{stroke} (\theta) = \| \epsilon - \epsilon_\theta (y_t, c, s, \sqrt{\vphantom{1} \bar{\alpha}_t}) \|_2^2 \\ L_\textrm{drawn} (\theta) = -d_0 \log (\hat{d}_0) - (1-d_0) \log (1-\hat{d}_0) \end{equation}\]

Pen-draw를 높은 noise level에서 예측하기 어렵기 때문에 pen-draw loss를 noise level에 따라 가중치를 주는 것이 좋다고 한다. 따라서 위의 pen-draw loss에 가중치 $\bar{\alpha}$를 준다.

Noise schedule을 어떻게 선택하는 지가 고품질 샘플을 생성하는 데에 중요하다. Wavegrad 논문에서는 이산적인 인덱스 $t$ 대신에 연속적인 noise level $\sqrt{\vphantom{1} \bar{\alpha}}$을 조건으로 주는 것을 제안하였으며, 재학습 없이 여러 noise schedule을 샘플링에서 사용할 수 있게 된다.

연속적인 noise level에서 신경망을 컨디셔닝하기 위하여 저자들은 먼저 noise schedule $l$을 정의하였다. $l_0 = 1$이고 \(l_t = \sqrt{\vphantom{1} \bar{\alpha}_t}\)라고 두고 \(t \sim \textrm{Uniform} (\{1,\cdots,T\})\)에 대하여 \(\sqrt{\vphantom{1} \bar{\alpha}} \sim \textrm{Uniform} (l_{t-1}, l_t)\)로 모델을 컨디셔닝한다.

손글씨 합성 신경망의 요구되는 목적 중 하나는 주어진 스타일로 손글씨를 생성하는 것이다. 이전 방법들은 특정 스타일의 샘플을 조건으로 주었다. 본 논문의 모델은 온라인 이미지를 생성하지만 오프라인 이미지도 조건을 받는다. 왜냐하면 온라인 이미지는 모으기가 어렵기 때문이다. 스타일 정보를 통합하기 위하여 Mobilenet으로 feature를 추출한다.

학습 알고리즘과 샘플링 알고리즘은 다음과 같다.

Model Architecture

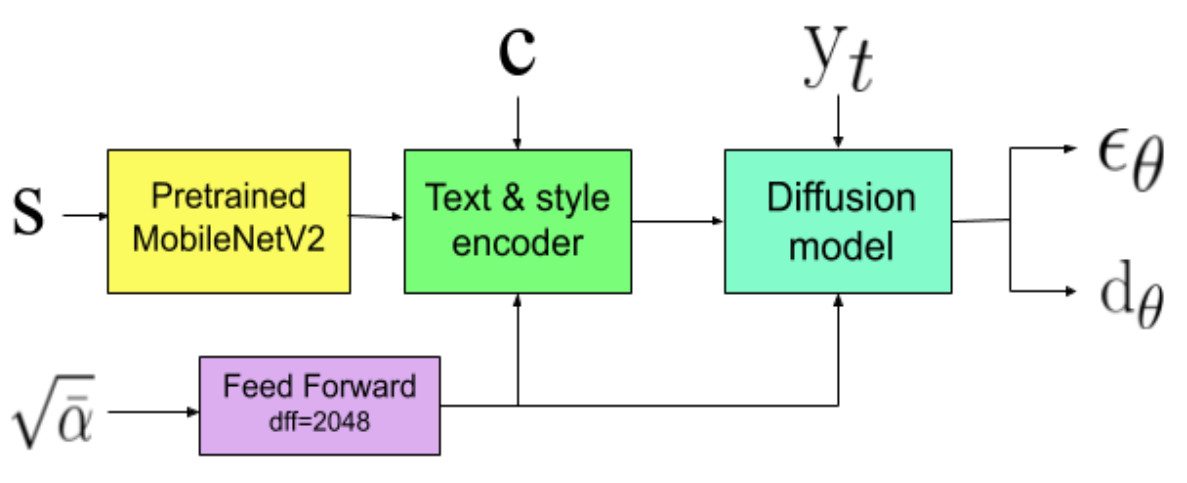
전체 모델은 위 그림과 같으며 두 부분으로 구성된다.

1. 목표 텍스트와 스타일 feature를 표현하는 텍스트와 스타일 인코더
2. $\epsilon_\theta$를 예측하는 diffusion probabilistic model

Noise level $\sqrt{\vphantom{1} \bar{\alpha}}$는 2개의 FC layer로 이루어진 feedforward network를 통과한 후 인코더와 diffusion model에 조건으로 주어진다.

Conditioning on the noise level

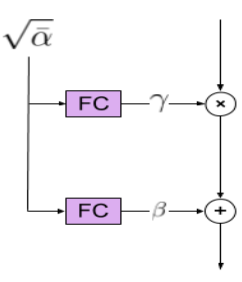
Noise level로 모델을 컨디셔닝하기 위하여 채널 축에 대한 affine transformation을 사용한다. 각 affine transformation의 scale과 bias는 FC layer의 출력이다.

Text and Style Conditioning

먼저 ImageNet에서 사전 학습된 MobileNetV2로 손글씨의 스타일 feature을 추출한다. 문자 수준의 임베딩으로 텍스트 시퀀스를 나타낸다. 그런 다음 텍스트 시퀀스와 추출된 feature 사이의 attention을 계산한다. 계산 결과를 feedforward network에 통과시키고 텍스트 시퀀스 표현에 더한다.

Diffusion model

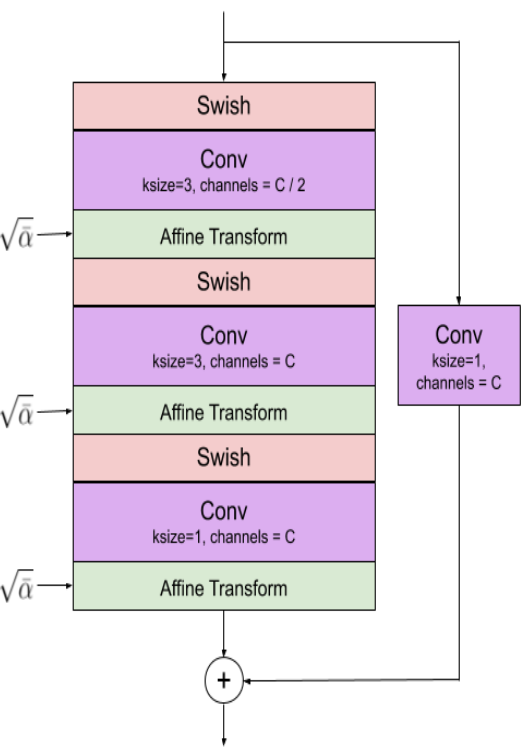
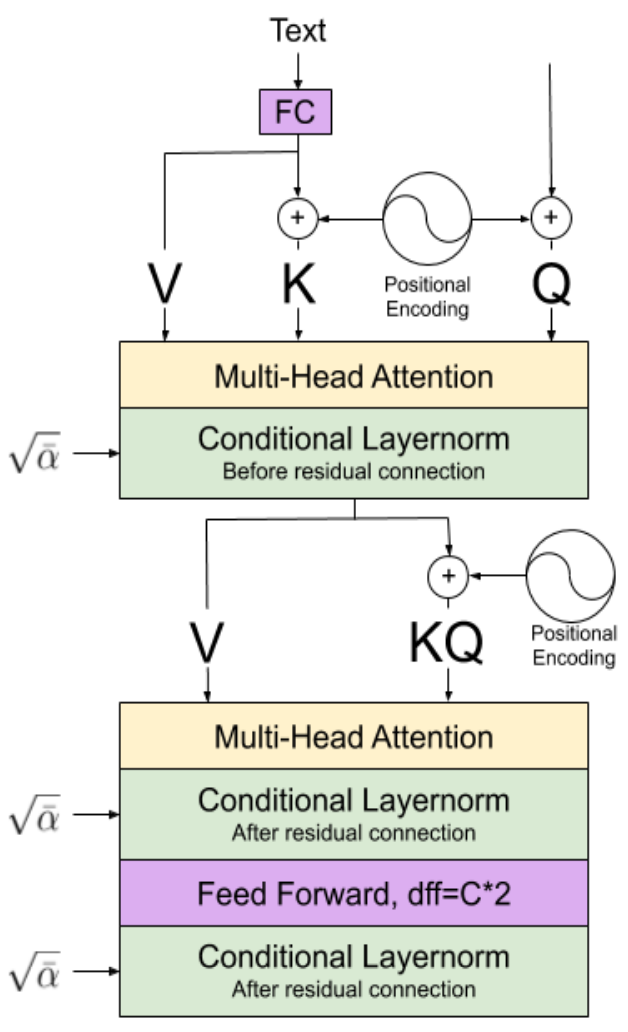
위 그림에서 왼쪽이 diffusion model, 가운데가 convolutional block, 오른쪽이 attention block이다.

Experiments

• 데이터셋
  • IAM Online Database (12000개의 손글씨 + 문자열 레이블)
  • 각 샘플은 동일한 사람의 손글씨 샘플과 연결되어 있음 (오프라인 이미지로 저장)
  • 평균보다 표준 편차가 15이상 큰 stroke를 포함한 샘플은 제외
• 학습
  • $T = 60$, $\beta_t = 0.02 + \exp (g)$ ($g$는 $10^{-5}$ ~ $0.4$)
  • 6만 step, batch size 96, NVIDIA V100, Adam optimizer ($\beta_1 = 0.9, \beta_2 = 0.98$), 기울기의 norm을 100으로 clip
  • 역제곱 learning rate schedule, 1만 warmup step
  • 모든 모델은 파라미터 1000만 개
• 평가 지표: FID, GS (Geometry Score) (둘 다 낮을수록 좋음)

다음은 Ground truth와의 객관적 평가 지표 비교이다.

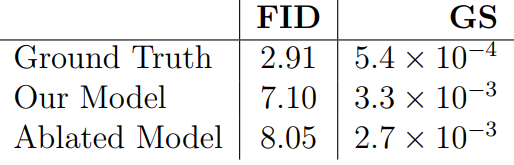
Ablated Model은 샘플링 시 기존 DDPM의 방식을 사용한 것으로, 본 논문의 방식이 성능 개선에 효과가 있음을 알 수 있다.

다음은 실제로 생성된 샘플들이다.

위의 4개는 테스트 데이터셋에 있는 실제 손글씨이고, 아래 8개는 랜덤하게 모델이 생성한 손글씨이다. 굉장히 손글씨의 품질이 좋은 것을 알 수 있다.

긴 텍스트 입력에 대하여 글자가 빠지거나 잘못된 글자를 포함하는 손글씨가 생성되지 않으려면 텍스트 시퀀스와 stroke 시퀀스가 align되는 것이 중요하다.

위의 그림에서 대각선은 stroke와 텍스트 시퀀스의 alignment를 예측한 것이다. 경험적으로 attention weight가 대각선에서 넓게 퍼지면 잘못된 글자를 생성한다. 텍스트가 알아보기 힘든 reverse process의 앞 부분에서도 attention weight가 잘 align되며 reverse process가 진행됨에 따라 잘 유지되는 것을 알 수 있다.

다음은 두 사람의 손글씨 샘플의 스타일을 interpolate하여 손글씨를 생성한 결과이다.

주어진 샘플 $s_0$와 $s_1$에 대하여 feature 벡터 $s_0’$와 $s_1’$을 각각 추출하고 모델에 $\hat{s} = \lambda s_0’ + (1-\lambda) s_1’$을 조건으로 준 것이다.