ICML 2021. [Paper] [Github] [Page]
Vadim Popov, Ivan Vovk, Vladimir Gogoryan, Tasnima Sadekova, Mikhail Kudinov
HUAWEI Noah’s Ark Lab | Higher School of Economics, Moscow, Russia.
13 May 2021
Introduction
최근 TTS는 두 부분의 신경망으로 디자인된다. 하나는 입력 텍스트를 시간-주파수 도메인의 음향 feature로 변환하는 feature generator이고, 다른 하나는 이런 feature를 raw waveform으로 변환하는 vocoder이다.
Tacotron2와 Transformer-TTS 등의 feature generator는 프레임 단위로 음향 feature를 생성하며 입력 텍스트로부터 거의 완벽한 mel-spectrogram 복원이 가능하다. 그럼에도 불구하고 계산적으로 효율적이지 못하고 attention failure에 의해 발생하는 발음 문제가 있다.
이러한 문제를 해결하기 위하여 FastSpeech나 Parallel Tacotron과 같은 모델은 non-autoregressive 아키텍처를 사용하고 추정된 토큰 길이로부터 hard monotonic alignment를 구축하였다. 반면 문자의 duration (발음되는 길이)을 학습시키려면 여전히 teacher model에서 미리 계산된 alignment가 필요하다. 최근 Non-Attentive Tacotron 프레임워크는 Variational Autoencoder 개념을 사용하여 duration을 학습하였다.
Glow-TTS feature generator는 Normalizing Flow를 기반으로 하여 발음과 계산 속도 문제를 극복하였다. Glow-TTS는 Monotonic Alignment Search (MAS) 알고리즘을 활용하여 입력 텍스트와 mel-spectrogram을 효율적으로 매핑하였다. 이 alignment는 기존 모델의 발음 문제를 피하기 위하여 의도적으로 디자인되었다.
Glow-TTS는 Transformer-TTS의 인코더 아키텍처를 사용하고 Glow의 디코더 아키텍처를 사용한다. Tacotron2와 비교했을 때 inference가 더 빠르고 잘못된 alignmnet가 더 적게 발생한다. 게다가 FastSpeech 같은 병렬적인 TTS 방법과 다르게 추가 aligner로 토큰 길이 정보를 얻을 필요가 없으며, 대신 MAS가 unsupervised한 방식으로 계산한다.
본 논문은 diffusion model의 개념을 사용한 score 기반 디코더로 구성된 feature generator인 Grad-TTS를 소개한다. MAS로 align된 인코더의 출력은 이러한 출력에 의해 parameterize된 가우시안 noise를 mel-spectrogram으로 변환하는 디코더로 전달된다.
가우시안 noise에서 데이터를 재구성하기 위하여 기존의 forward diffusion과 reverse diffusion을 일반화한다. Grad-TTS의 한 가지 특징은 mel-spectrogram의 품질과 inference 속도 사이의 trade-off를 조절할 수 있다는 것이다.
특히, Grad-TTS는 10번의 reverse diffusion만으로 고품질의 mel-spectrogram을 생성할 수 있으며, 이는 Tacotron2의 속도를 능가한다. 또한 output 도메인을 mel-spectrogram에서 raw waveform으로 바꾸면 Grad-TTS를 end-to-end TTS 파이프라인으로 학습할 수 있다는 것을 보였다.
Diffusion probabilistic modelling
Diffusion process는 stochastic differential equation (SDE)
\[\begin{equation} dX_t = b(X_t, t)dt + a(X_t, t) dW_t \end{equation}\]를 만족하는 stochastic processs이다. 여기서 $W_t$는 표준 브라운 운동이며 $t \in [0, T]$와 계수 $b$와 $a$는 특정 조건을 만족한다.
임의의 데이터 분포 $Law (X_0)$에 대하여 $T$가 무한대로 갈 때 마지막 분포 $Law (X_T)$가 표준 정규분포 $\mathcal{N}(0, I)$로 수렴하는 stochastic process는 찾기 쉽다. 사실은 굉장히 많은 process가 이를 만족한다. 이러한 속성을 만족하는 process를 forward diffusion이라 하며 diffusion 모델링의 목표는 forward diffusion과 궤적이 거의 같으면서 역방향 시간 순서인 reverse diffusion을 찾는 것이다.
이는 어렵지만 reverse diffusion을 적절한 신경망으로 parameterize하면 할 수 있다. 이 경우 random noise $\mathcal{N}(0,I)$에서 시작하여 아무 numerical solver로 단순히 reverse diffusion의 SDE를 풀면 된다. 만일 forward diffusion과 reverse diffusion이 가까운 궤적을 가지면 샘플링 결과의 분포는 데이터 분포와 가깝다.
이러한 생성 모델링의 접근 방식은 다음과 같다.
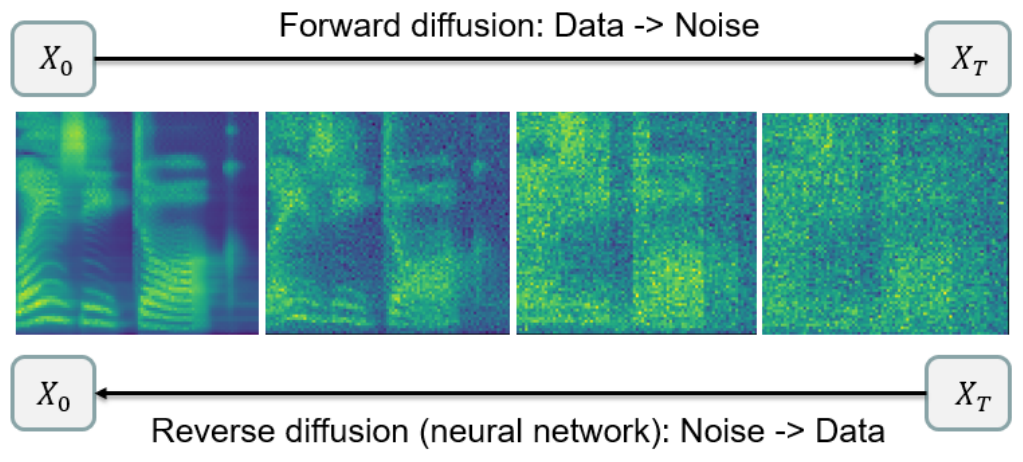
최근까지 score 기반인 DDPM은 Markov chain으로 구성되었다. Score-Based Generative Modeling through SDEs 논문 (Paper review)에서는 이 Markov chain이 특정 SDE를 만족하는 stochastic process의 궤적을 근사한다고 설명한다.
본 논문에서는 이 논문을 따라 Markov chain 대신 SDE로 DPM을 정의한다. 또한 무한한 $T$에 대해 forward diffusion이 모든 데이터 분포를 $\mathcal{N}(0,I)$ 대신 주어진 임의의 평균 $\mu$와 대각 공분산 행렬 $\Sigma$에 대하여 $\mathcal{N}(\mu, \Sigma)$로 변환하는 방식으로 DPM을 일반화하는 것을 제안한다.
1. Forward diffusion
먼저 임의의 데이터를 가우시안 noise로 변환하는 forward diffusion process를 정의해야 한다. 만일 $n$ 차원의 stochastic process $X_t$가 noise schedule라 부르는 음이 아닌 함수 $\beta_t$, 벡터 $\mu$, 양의 원소로 이루어진 대각 행렬 $\Sigma$에 대하여 SDE
\[\begin{equation} dX_t = \frac{1}{2} \Sigma^{-1} (\mu - X_t) \beta_t dt + \sqrt{\beta_t} dW_t, \quad t \in [0, T] \end{equation}\]를 만족하고 해가 존재하면, 해는 다음과 같다.
\[\begin{equation} X_t = \bigg( I - e^{-\frac{1}{2}\Sigma^{-1} \int_0^t \beta_s ds} \bigg) \mu + e^{-\frac{1}{2}\Sigma^{-1} \int_0^t \beta_s ds} X_0 + \int_0^t \sqrt{\beta_s} e^{-\frac{1}{2}\Sigma^{-1} \int_0^t \beta_u du} dW_s \end{equation}\]대각 행렬의 exponential은 단순히 element-wise exponential이다.
\[\begin{equation} \rho (X_0, \Sigma, \mu, t) = \bigg( I - e^{-\frac{1}{2}\Sigma^{-1} \int_0^t \beta_s ds} \bigg) \mu + e^{-\frac{1}{2}\Sigma^{-1} \int_0^t \beta_s ds} X_0 \\ \lambda(\Sigma, t) = \Sigma \bigg( I - e^{-\Sigma^{-1} \int_0^t \beta_s ds} \bigg) \end{equation}\]라 두면, Ito의 적분 조건부 분포의 특성에 의해
\[\begin{equation} Law (X_t \vert X_0) = \mathcal{N} (\rho (X_0, \Sigma, \mu, t), \lambda (\Sigma, t)) \end{equation}\]이다. 무한한 시간을 생각했을 때 $e^{-\int_0^\infty \beta_s ds} = 0$인 임의의 nosie schedule $\beta_t$에 대하여 $Law (X_t \vert X_0)$는 $\mathcal{N}(\mu, \Sigma)$로 수렴한다.
2. Reverse diffusion
기존 DPM reverse diffusion에 대한 연구는 forward diffusion의 궤적을 근사하도록 학습되었다. Diffusion 종류의 stochastic process의 역시간 역학 공식은 이미 유도되어 있다. 이를 이용하여 reverse diffusion의 SDE를 구하면 다음과 같다.
\[\begin{equation} dX_t = \bigg( \frac{1}{2} \Sigma^{-1} (\mu - X_t) - \nabla \log p_t (X_t) \bigg) \beta_t dt + \sqrt{\beta_t} d \tilde{W_t}, \quad t \in [0, T] \end{equation}\]$\tilde{W_t}$는 역시간 브라운 운동이며 $p_t$는 $X_t$의 확률 밀도 함수이다. 이 SDE는 종단 조건 $X_T$에서 시작하여 거꾸로 풀어야 한다.
Score-Based Generative Modeling through SDEs 논문에서는 위의 SDE를 사용하는 대신 다음과 같은 ODE (상미분방정식)를 고려한다.
\[\begin{equation} dX_t = \frac{1}{2} \bigg(\Sigma^{-1} (\mu - X_t) - \nabla \log p_t (X_t) \bigg) \beta_t dt \end{equation}\]Forward diffusion에 대한 SDE의 forward Kolmogorov equation은 위의 SDE와 동일하다. 이는 두 SDE에 의한 stochastic process들의 확률 밀도 함수가 같다는 것을 의미한다.
따라서 $\nabla \log p_t (X_t)$를 추정하는 신경망 $s_\theta (X_t, t)$이 있다면, $\mathcal{N}(\mu, \Sigma)$에서 $X_T$를 샘플링하고 numerical solver로 시간을 거꾸로하여 위의 SDE를 풀면 데이터 분포 $Law (X_0)$를 모델링할 수 있다.
3. Loss function
$X_t$의 로그 밀도의 기울기를 추정하는 것은 score matching이라고 불리며, 최근 논문에서는 $L_2$ loss로 이 기울기를 신경망으로 근사시킨다. 따라서 본 논문은 같은 종류의 loss를 사용한다.
$Law (X_t \vert X_0)$의 식에 의해 $X_t$를 주어진 초기 데이터 $X_0$만으로 샘플링할 수 있다. 또한, $Law (X_t \vert X_0)$는 가우시안이므로 로그 밀도는 굉장히 간단한 closed form이다.
만일 $\mathcal{N}(0, \lambda(\Sigma, t))$에서 $\epsilon_\theta$를 샘플링한 다음
\[\begin{equation} X_t = \rho (X_0, \Sigma, \mu, t) + \epsilon_t \end{equation}\]에 대입하면 $X_t$의 로그 밀도의 기울기는
\[\begin{equation} \nabla \log p_{0t} (X_t \vert X_0) = - \lambda (\Sigma, t)^{-1} \epsilon_t \end{equation}\]이다. 여기서 $p_{0t}(\cdot \vert X_0)$는 조건부 분포의 확률 밀도 함수이다.
따라서 시간 $t$에 의해 noise가 누적되어 손상되는 $X_0$의 로그 밀도의 기울기를 추정하는 손실 함수는 다음과 같다.
\[\begin{equation} \mathcal{L}_t (X_0) = \mathbb{E}_{\epsilon_t} \bigg[ \| s_\theta (X_t, t) + \lambda(\Sigma, t)^{-1} \epsilon_t \|_2^2 \bigg] \end{equation}\]Grad-TTS
Grad-TTS의 접근 방식은 다음과 같다.
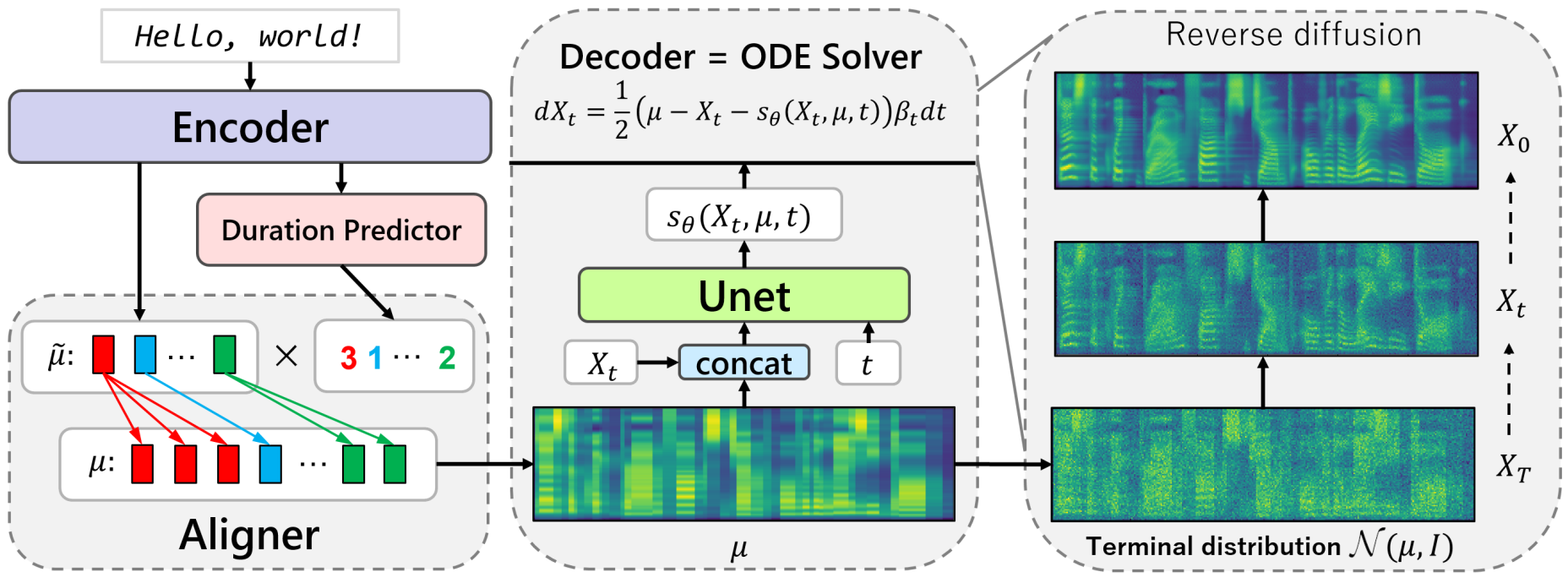
Grad-TTS는 Glow-TTS와 비슷한 점이 많으며, 주요 차이점은 디코더이 어떤 규칙을 따르는 지이다.
1. Inference
길이가 $L$인 입력 텍스트 시퀀스 $x_{1:L}$는 일반적으로 문자나 음소로 이루어져 있으며, 음향 프레임이 $F$개 있을 때 mel-spectrogram $y_{1:F}$를 생성하는 것이 목표이다.
Grad-TTS에서는 duration predictor로 $x_{1:L}$를 feature의 시퀀스 \(\tilde{\mu}_{1:L}\)로 변환한다. 이를 통해 \(\tilde{\mu}_{1:L}\)와 프레임별 feature \(\mu_{1:F}\) 사이의 hard monotonic alignment $A$를 생성한다. 함수 $A$는 $[1, F] \cap \mathbb{N}$과 $[1, L] \cap \mathbb{N}$ 사이의 단조 전사 매핑 (monotonic surjective mapping)이다. 즉, 임의의 정수 $j \in [1, F]$에 대하여 $\mu_j = \tilde{\mu}_A(j)$로 매핑한다.
Duration predictor는 입력 텍스트의 각 요소가 얼마나 많은 프레임만큼 지속되는 지를 계산한다. $A$가 단조 함수이고 전사 함수이기 때문에 텍스트가 빠짐 없이 모두 정확한 순서로 발음되는 것이 보장된다. Duration predictor를 사용하는 모든 TTS 모델은 duration에 특정 값을 곱하여 합성되는 음성의 템포를 조절할 수 있다.
그런 다음 출력 시퀀스 $\mu = \mu_{1:F}$는 DPM으로 구성된 디코더를 통과한다. 신경망 $s_\theta (X_t, \mu, t)$로 ODE
\[\begin{equation} dX_t = \frac{1}{2} (\mu - X_t - s_\theta (X_t, \mu, t)) \beta_t dt \end{equation}\]를 정의할 수 있으며, 이 ODE는 역시간 방향에 대하여 1차 오일러 방법을 사용하여 풀 수 있다. $\mu$는 종단 조건 $X_t \sim \mathcal{N} (\mu, I)$를 정의하는 데에도 사용된다.
$\beta_t$와 $T$는 미리 정의된 hyper-parameter이며, 데이터에 따라 다르게 선택된다. 오일러 방법의 step size $h$는 학습이 끝난 후 선택해도 되는 hyper-parameter이다. $h$는 mel-spectrogram의 품질과 inference 속도 사이의 trade-off를 조절하는 데 사용된다.
위의 ODE가 선택된 과정은 다음과 같다.
- Reverse diffusion에 대하여 SDE 대신 ODE를 사용하는 것이 더 좋은 결과를 나타냈다.
작은 $h$를 사용하면 비슷한 결과가 나타났으며, 큰 $h$를 사용하면 ODE가 더 좋은 사운드 결과를 보였다고 한다. - $\Sigma = I$를 사용하여 전체 feature generator 파이프라인을 간소화하였다.
- $\mu$를 $s_\theta$에 추가 입력으로 주었다.
이는 $s_\theta$가 $X_t$만을 가지고 $X_0$에 추가된 가우시안 noise를 예측해야 하므로 noise의 극한 $\lim_{T \rightarrow \infty} Law(X_T \vert X_0)$가 어떻게 생겼는지를 추가 지식으로 제공하는 것이다. noise의 극한은 텍스트 입력에 따라 달라지므로 $s_\theta$가 더 정확한 noise 예측을 할 수 있도록 도와준다.
추가로 저자들은 temperature hyper-parameter $\tau$를 사용하여 $X_T$를 $\mathcal{N} (\mu, I)$ 대신 $\mathcal{N} (\mu, \tau^{-1}I)$에서 샘플링하였을 때 이점이 있음을 발견하였다. $\tau$를 튜닝하여 출력되는 mel-spectrogram의 품질을 유지하면서 step size $h$를 키울 수 있다고 한다.
2. Training
Grad-TTS의 하나의 목적 함수는 align된 인코더의 출력 $\mu$와 target mel-spectrogram $y$의 거리를 최소화하는 것이다. 이는 inference 단계에서 $\mathcal{N}(\mu, I)$에서 디코딩을 시작하기 때문이다. 직관적으로 target $y$에 이미 가까운 noise에서 디코딩을 시작하는 것이 더 쉽다.
만일 $\mu$로 디코더의 시작 입력 noise를 parameterize한다면, 인코더의 출력 $\tilde{\mu}$를 정규분포 $\mathcal{N}(\tilde{\mu}, I)$로 생각할 수 있다. 따라서 NLL 인코더 loss
\[\begin{equation} \mathcal{L}_{enc} = - \sum_{j=1}^F \log \psi (y_j ; \tilde{\mu}_{A(j)}, I) \end{equation}\]를 사용할 수 있다. 여기서 $\psi(\cdot; \tilde{\mu}_i, I)$는 $\mathcal{N}(\tilde{\mu}_i, I)$의 확률 밀도 함수이다.
다른 형태의 loss도 사용할 수 있지만, \(\mathcal{L}_{enc}\)를 사용하지 않으면 alignment 학습에 실패하는 것을 실험에서 확인했다고 한다.
\(\mathcal{L}_{enc}\)는 인코더의 파라미터와 alignment 함수 $A$를 동시에 최적화한다. 동시에 최적화하는 것이 어렵기 때문에 Glow-TTS의 iterative한 방법을 사용하였다. 최적화의 각 iteration은 두 단계로 이루어진다.
- 인코더의 파라미터를 고정하고 최적의 alignment $A^\ast$를 찾는다. → MAS 알고리즘 사용
- $A^\ast$를 고정하고 SGD 한 step을 수행하여 인코더의 파라미터에 대하여 손실 함수를 최적화한다.
Grad-TTS는 inference 단계에서 $A^\ast$를 추정하기 위하여 duration predictor 신경망 $DP$를 사용한다. $DP$는 로그 도메인에서의 MSE를 사용하여 학습시킨다.
\[\begin{equation} d_i = \log \sum_{j=1}^F \mathbb{I}_{A^\ast (j) = i}, \quad i = 1, \cdots, L \\ \mathcal{L}_{dp} = MSE(DP(sg[\tilde{\mu}]), d) \end{equation}\]여기서 $\mathbb{I}$는 indicator function이며, \(\tilde{\mu} = \tilde{\mu}_{1:L}\), \(d = d_{1:L}\)이고 $sg[\cdot]$는 \(\mathcal{L}_{dp}\)가 인코더의 파라미터에 영향을 주지 못하도록 하는 stop gradient operator이다.
DPM 학습을 위한 loss는 앞에서 설명한 loss를 쓴다. $\Sigma = I$를 사용하기 때문에 공분산 행렬도 단순하게 항등 행렬 $I$에
\[\begin{equation} \lambda_t = 1 - e^{-\int_0^t \beta_s ds} \end{equation}\]를 곱한 꼴이 된다. 전체 diffusion 손실 함수 \(\mathcal{L}_{diff}\)는 서로 다른 시간 $t \in [0, T]$에서의 로그 밀도의 기울기 추정과 관련된 가중 손실의 기대치이다.
\[\begin{equation} \mathcal{L}_{diff} = \mathbb{E}_{X_0, t} \bigg[ \lambda_t \mathbb{E}_{\xi_t} \bigg[ \bigg\| s_\theta (X_t, \mu, t) + \frac{\xi_t}{\sqrt{\lambda_t}} \bigg\|_2^2 \bigg] \bigg] \end{equation}\]$X_0$는 학습 데이터에서 뽑은 target mel-spectrogram $y$를 의미하며, $t$는 $[0, T]$에서 uniform하게 뽑고 $\xi_t$는 $\mathcal{N}(0, I)$에서 뽑는다.
또한 다음 식을 사용하여 $X_t$를 뽑는다.
\[\begin{equation} X_t = \rho (X_0, I, \mu, t) + \sqrt{\lambda_t} \xi_t \end{equation}\]위의 두 식은 $\epsilon_t = \sqrt{\lambda_t} \xi_t$으로 대입하여 구할 수 있다. $\mathcal{L}_t (X_0)$ 식의 가중치로 $\lambda_t$를 사용하며 이 가중치는
\[\begin{equation} \frac{1}{\mathbb{E} [\| \nabla \log p_{0t} (X_t \vert X_0) \|_2^2]} \end{equation}\]에 비례해야 한다. 정리하면 전체 학습 과정은 다음과 같다.
- 인코더, duration predictor, 디코더를 고정하고 MAS 알고리즘으로 \(\mathcal{L}_{enc}\)를 최소화하는 alignment $A^\ast$를 찾는다.
- $A^\ast$를 고정하고 \(\mathcal{L}_{enc} + \mathcal{L}_{dp} + \mathcal{L}_{diff}\)를 최소화하여 인코더, duration predictor, 디코더를 학습시킨다.
- 위 2개의 step을 수렴할 때까지 반복한다.
3. Model architecture
인코더와 duration predictor는 Glow-TTS와 동일한 아키텍처를 사용하며, 각각 Transformer-TTS와 FastSpeech에서 구조를 차용한다.
Duration predictor는 2개의 conv layer와 projection layer로 구성되어 duration의 로그를 예측한다. 인코더는 pre-net, 6개의 Transformer block, linear projection layer로 구성된다. Pre-net은 3개의 conv layer와 FC layer로 구성된다.
디코더 신경망 $s_\theta$는 DDPM과 같게 U-Net 아키텍처를 사용하여 32$\times$32 이미지를 생성하며, DDPM과 달리 2배 작은 채널 수와 4개 대신 3개의 feature map resolution을 사용하여 모델 크기를 줄인다. 또한 $80 \times F$, $40 \times F/2$, $20 \times F/4$에서 작동한다. 만일 $F$가 4의 배수가 아니면 zero-pad mel-spectrogram을 사용한다. $\mu$는 $X_t$와 concat되서 U-Net에 입력된다.
Experiments
- 데이터셋: LJSpeech (24시간 분량의 영어 여성 목소리, 22.05kHz), 테스트셋에는 10초 미만의 오디오 500개 사용
- 입력 텍스트는 음소로 분리되어 인코더에 입력
- Mel-spectrogram은 정규화하는 것보다 그냥 사용하는 것이 성능이 좋다고 함
- 170만 iteration, NVIDIA RTX 2080 Ti 1개, mini-batch size 16, Adam optimizer (lr = 0.0001)
- 학습에서 중요한 점
- $T = 1$, $\beta_t = \beta_0 + (\beta_1 - \beta_0)t$, $\beta_0 = 0.05$, $\beta_1 = 20$
- Mel-spectrogram에서 랜덤하게 2초를 뽑아 target $y$로 사용하여 메모리 효율적으로 학습. MAS와 duration predictor는 전체 mel-spectrogram 사용.
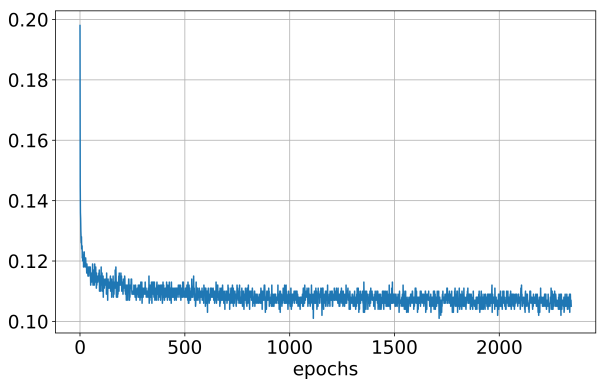
- \(\mathcal{L}_{diff}\)는 굉장히 느리게 수렴하므로 긴 학습이 필요. 같은 loss의 모델이어도 생성되는 mel-spectrogram의 품질이 굉장히 다르다고 함.
1. Subjective & objective evaluation
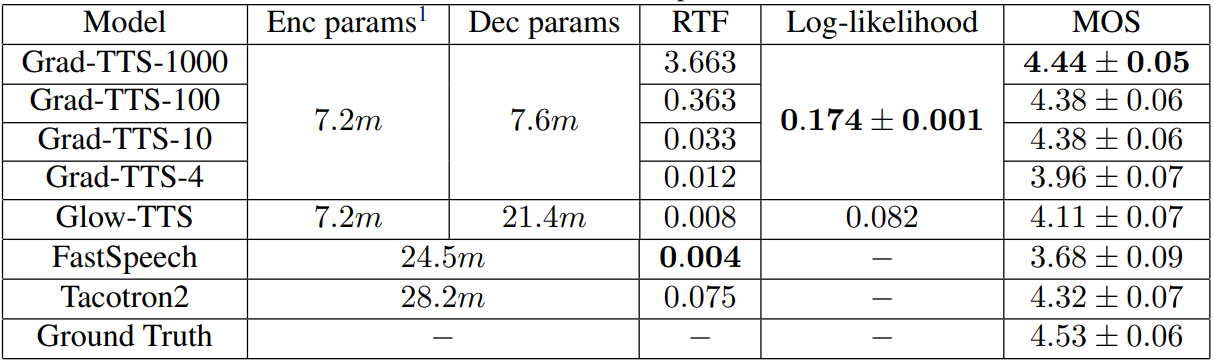
주관적 평가 지표로는 테스트셋에서 40 문장씩 합성하여 Mean Opinion Score (MOS)를 10명으로부터 측정하였다. 객관적 평가 지표로는 테스트셋에서 50 문장씩 뽑아 평균 log-likelihood를 측정하였다.
다음은 $\mathcal{N}(\mu, I)$에서 시작하는 Grad-TTS-10을 baseline으로 하였을 때 $\mathcal{N}(0, I)$에서 시작하는 Grad-TTS의 성능을 주관적으로 평가한 것이다.
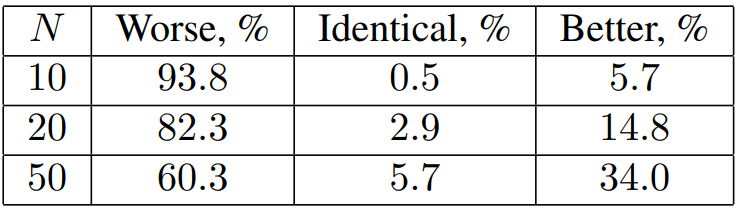
$\mathcal{N}(\mu, I)$에서 시작하는 것이 더 성능이 좋은 것을 볼 수 있으며, $\mathcal{N}(0, I)$에서 시작하는 경우 더 많은 step으로 ODE solver를 사용해야 한다는 것을 알 수 있다.
2. Efficiency estimation
다음은 텍스트 길이에 따른 inference 속도 비교이다.








![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)