Blogs

JMLR 2021. [Paper] [Page]
Jonathan Ho, Chitwan Saharia, William Chan, David J. Fleet, Mohammad Norouzi, Tim Salimans
Google Brain
30 May 2021

Introduction

기존 diffusion model은 고품질의 이미지 생성의 가능성을 보였으며, 어느 정도 크기의 데이터셋이나 강하게 컨디셔닝이 가능한 데이터를 사용하였다. 본 논문은 강한 컨디셔닝 없이 고해상도에서 diffusion model의 샘플 품질을 개선하는 것을 목표로 한다. 기존 diffusion model의 가능성을 보여주기 위해 추가 classifer 등을 사용하지 않고 간단하고 직접적인 방법으로 샘플 품질을 향상시킨다.

본 논문은 계단식으로 class-conditional ImageNet에서 샘플의 품질을 개선한다. “계단식”은 여러 해상도에서 개별적으로 학습된 모델의 파이프라인을 학습하여 고해상도 데이터를 모델링하는 간단한 기술을 의미한다. 기본 모델은 저해상도 샘플을 생성한 다음 저해상도 샘플을 고해상도 샘플로 upsampling하는 super-resolution 모델을 사용한다. 아무 생성 모델이나 계단식 파이프라인에 사용할 수 있지만 본 논문에서는 diffusion model만을 사용한다.

간단하면서도 가장 효과적인 방법은 강한 데이터 augmentation을 각 super-resolution 모델의 컨디셔닝 입력으로 주는 것이다. 이 방법을 conditioning augmentation이라 부른다. Conditioning augmentation은 노출 편향이라고도 하는 train-test 불일치로 인한 계단식 파이프라인의 복합 오류를 완화하기 때문에 고품질 샘플 생성에 효과적이다.

Conditioning Augmentation in Cascaded Diffusion Models

$x_0$를 고해상도 데이터, $z_0$를 저해상도 데이터라 가정하자. 저해상도에서는 diffusion model $p_\theta(z_0)$를 사용하며, 고해상도에서는 super-resolution model $p_\theta (x_0 \vert x_0)$를 사용한다. 계단식 파이프라인은 다음과 같이 latent variable model을 형성한다.

\[\begin{equation} p_\theta (x_0) = \int p_\theta (x_0 | z_0) dz_0 \end{equation}\]

당연하게도 둘보다 더 많은 해상도로 이를 확장할 수 있으며, 모든 계단식 파이프라인에 클래스 정보나 다른 컨디셔닝 정보 $c$를 줄 수 있다.

계단식 파이프라인의 예시는 다음과 같다.

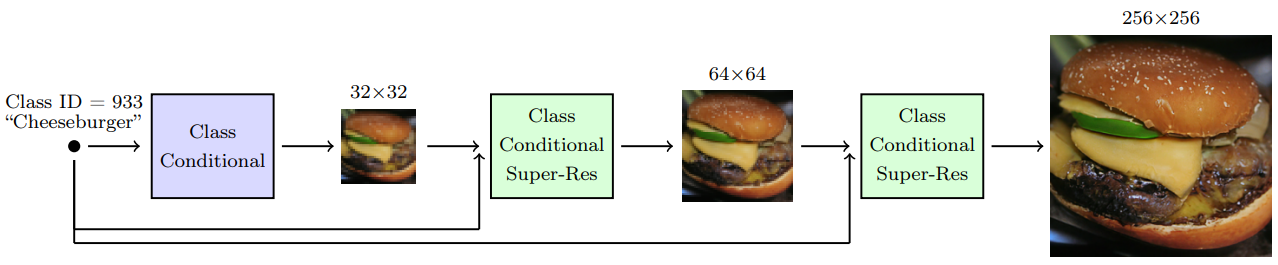
계단식 파이프라인은 다른 생성 모델에서도 유용하다. 고해상도에서 계단식 파이프라인을 학습시킬 떄의 가장 큰 이점은 대부분의 modeling capacity가 샘플링에서 가장 중요하며 계산적으로 효율적인 저해상도에 사용된다는 것이다. 또한, 계단식 파이프라인은 각 모델이 독립적으로 학습될 수 있도록 하며, 각 해상도에서 최상의 성능을 위해 튜닝이 가능하다.

계단식 파이프라인의 샘플 품질을 개선하기 위한 가장 효과적인 방법은 저해상도 입력에서 data augmentation을 사용하여 각 super-resolution 모델을 학습시키는 것이다. 이를 conditional augmentation이라 한다. Super-resolution 모델 $p_\theta (x_0 \vert z)$가 저해상도 이미지 $z$에서 고해상도 이미지 $x_0$를 생성할 때 $z$에 어떤 형식의 data augmentation을 적용하는 것이다.

이 augmentation은 어떤 형식도 사용할 수 있으며, 저자들이 찾은 가장 효과적인 방법은 저해상도에서는 가우시안 noise를 추가하고 고해상도에서는 $z$에 가우시안 blur를 랜덤하게 적용하는 것이다. 어떤 경우에는 conditioning augmentation의 강도에 대해 super-resolution 모델을 학습시키고 학습 후 최적의 샘플 품질을 위한 하이퍼파라미터 검색에서 최고의 강도를 선택하는 것이 더 실용적이다.

1. Blurring Augmentation

간단한 conditioning augmentation의 하나는 $z$에 blur를 적용하는 것이다. 저자들은 128$\times$128이나 256$\times$256으로의 upsampling 시에 blurring augmentation이 가장 효과적임을 확인하였다. 저자들은 커널 크기 $k = (3, 3)$를 사용하였고 고정된 범위에서 랜덤으로 $\sigma$를 샘플링하여 사용하였다. 학습 시에는 blurring augmentation을 50%만큼 사용하였으며, inference에서는 저해상도 입력에 augmentation을 사용하지 않았다.

2. Truncated Conditioning Augmentation

Truncated conditioning augmentation은 저해상도의 reverse process를 timestep $s > 0$에서 멈추고 멈춘 timestep의 샘플을 super-resolution 모델에 조건으로 주는 방법이다.

기본 모델은

\[\begin{equation} p_\theta (z_s) = \int p_\theta (z_{s:T}) p_\theta (z_s) dz_{s+1:T} \end{equation}\]

이며 super-resolution 모델은

\[\begin{equation} p_\theta (x_0 | z_s) = \int p(x_T) \prod_{t=1}^T p_\theta (x_{t-1} | x_t, z_s) dx_{1:T} \\ p_\theta (x_{t-1} | x_t, z_s) = \mathcal{N} (x_{t-1} ; \mu_\theta (x_t, t, z_s, s), \Sigma_\theta (x_t, t, z_s, s)) \end{equation}\]

가 되어 전체 샘플링은

\[\begin{equation} p_\theta^s (x_0) = \int p_\theta (x_0 | z_s) p_\theta (z_s) dz_s = \int p_\theta (x_0 | z_s) p_\theta (z_{s:T}) dz_{s:T} \end{equation}\]

이 된다.

따라서 truncated conditioning augmentation은 학습과 super-resolution 모델의 아키텍처에 간단한 수정이 필요한 augmentation이며 첫번째 저해상도 모델은 수정이 필요없다. 이 방법은 128$\times$128보다 작은 해상도에서 가장 유용하다.

저해상도의 reverse process를 자르는 것이 data augmentation인 이유는 $p_\theta (x_0 \vert z_s)$가 $z_0$를 가우시안 noise로 증강한 것이기 때문이다.

$p_\theta^s (x_0)$을 diffusion model prior, diffusion model decoder, 그리고 해상도에 독립적으로 forward process를 실행하는 approximate posterior

\[\begin{equation} q(x_{1:T}, z_{1:T} | x_0, z_0) = \prod_{t=1}^T q(x_t | x_{t-1}) q(z_t | z_{t-1}) \end{equation}\]

로 이루어진 VAE로 생각할 수 있다.

따라서 $p_\theta^s (x_0)$의 ELBO는 다음과 같다.

\[\begin{equation} - \log p_\theta^s (x_0) \le \mathbb{E}_q \bigg[ L_T (z_0) + \sum_{t > s} D_\textrm{KL} (q(z_{t-1} | z_t, z_0) \; \| \; p_\theta(z_{t-1} | z_t)) - \log p_\theta (x_0 | z_s) \bigg] \end{equation}\]

여기서 $L_T (z_0) = D_\textrm{KL} (q(z_T \vert z_0) \vert\vert p(z_T))$이다. Diffusion model decoder의 ELBO는 다음과 같다.

\[\begin{equation} - \log p_\theta (x_0 | z_s) \le L_\theta (x_0 | z_s) = \mathbb{E}_q \bigg[ L_T (x_0) + \sum_{t > 1} D_\textrm{KL} (q(x_{t-1} | x_t, x_0) \; \| \; p_\theta(x_{t-1} | x_t, z_s)) - \log p_\theta (x_0 | x_1, z_s) \bigg] \end{equation}\]

이를 대입하면 전체 ELBO를 다음과 같이 구할 수 있다.

\[\begin{equation} - \log p_\theta^s (x_0) \le \mathbb{E}_q \bigg[ L_T (z_0) + \sum_{t > s} D_\textrm{KL} (q(z_{t-1} | z_t, z_0) \; \| \; p_\theta(z_{t-1} | z_t)) + L_\theta (x_0 | z_s) \bigg] \end{equation}\]

위 식을 최적화하면 저해상도 모델과 고해상도 모델을 별도로 학습시킬 수 있다는 것이 분명하다. 고정된 $s$에 대하여 저해상도 process는 timestep $s$까지 학습되고 super-resolution 모델은 이 손상된 신호를 조건으로 학습된다.

실제로는 위의 ELBO 식을 직접 모델 학습에 사용하지 않고 DDPM 논문에서처럼 가중치를 제거한 간단한 loss를 사용한다. 저자들은 최고의 샘플 품질을 위한 $s$를 찾아 사용하려고 하였다. 왜냐하면 임의의 $s$에 대하여 super-resolution model을 학습시키는 경우 $s$를 위한 추가 time embedding이 필요하기 때문이다. 저해상도 모델은 이미 임의의 $s$로 학습되고 있으므로 모델 아키텍처를 변경할 필요가 없다.

3. Non-truncated Conditioning Augmentation

Non-truncated conditioning augmentation은 저해상도 중간에 멈추지 않고 $z_0$까지 샘플링한 다음 저해상도 샘플을 forward process로 손상시키는 방법이다. Truncated augmentation과 동일한 모델을 사용하며, 유일한 차이점은 샘플링 시간이다.

이 방법의 주요 장점은 $s$ 이상의 검색 단계에서 실용적이라는 것이다. Truncated augmentation의 경우 모든 $s$에 대하여 super-resolution 모델을 병렬로 실행하려면 모든 $z_s$를 저장해야 하지만, 이 방법의 경우 $z_0$ 하나만 저장하고 $z_s$를 forward process로 샘플링하면 된다.

다음은 위의 두 가우시안 conditioning augmentation의 학습과 샘플링 알고리즘이다.

Experiments

1. Main Cascading Pipeline Results

다음 표는 class-conditional ImageNet에서 classifier guidance를 사용하지 않은 모델들과의 샘플 품질을 비교한 결과이다.

다음은 256$\times$256 ImageNet에서의 샘플 품질과 다양성의 비교 결과이다.

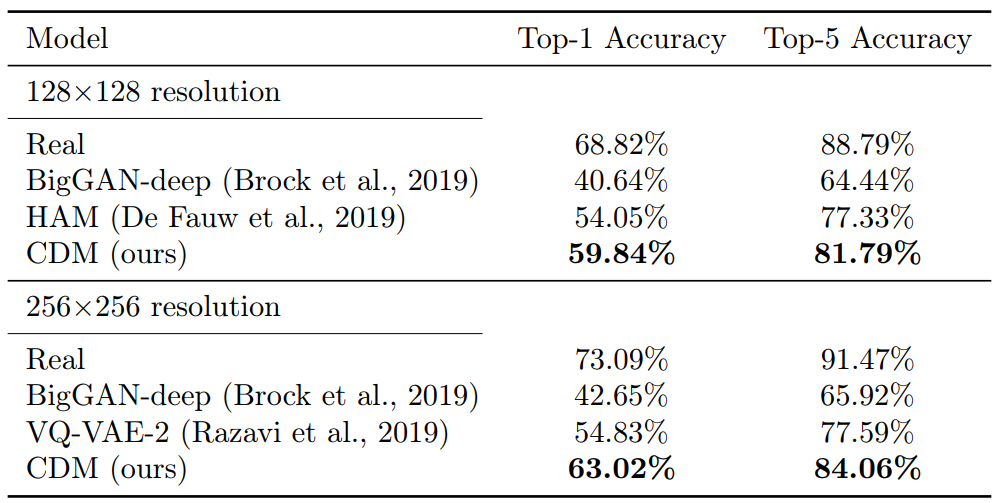
다음 표는 128$\times$128과 256$\times$256에서의 Classification Accuracy Score (CAS) 결과이다.

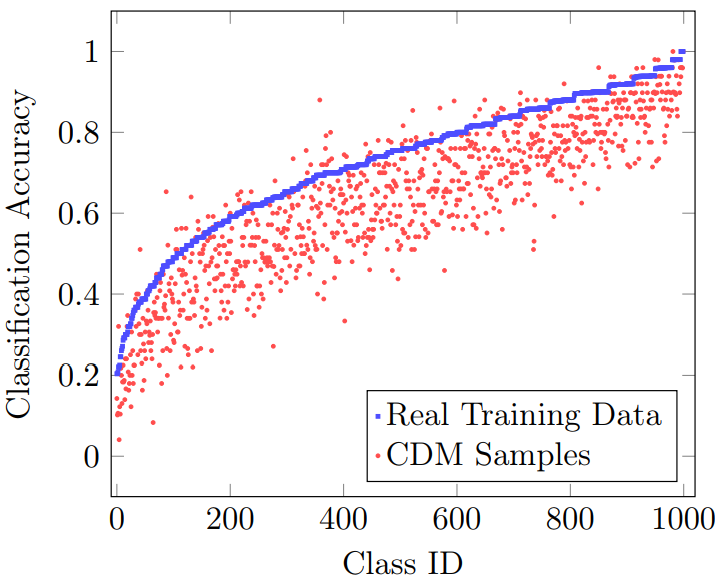
다음은 각 클래스 별 CAS이다. (256$\times$256 해상도)

2. Baseline Model Improvements

다음 표는 64$\times$64 ImageNet에서 Improved DDPM에 dropout을 추가하고 2000 timestep으로 더 오래 학습시킨 개선 결과이다.

3. Conditioning Augmentation Experiments up to 64×64

다음 표는 개선시킨 Improved DDPM에 16$\times$16에서 64$\times$64로의 계단식 파이프라인을 사용하였을 때의 개선 결과이다.

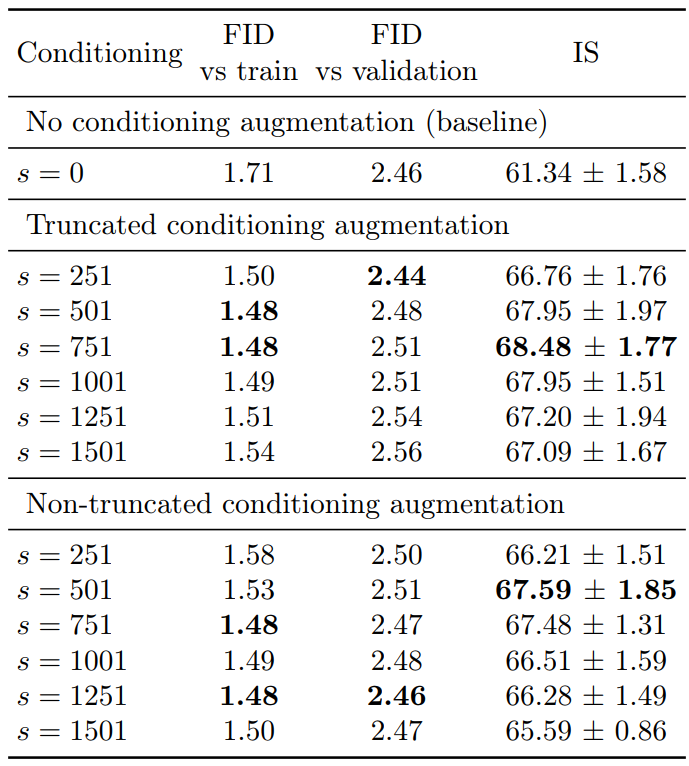
다음 표는 truncated augmentation과 non-truncated augmentation의 샘플 품질이다.

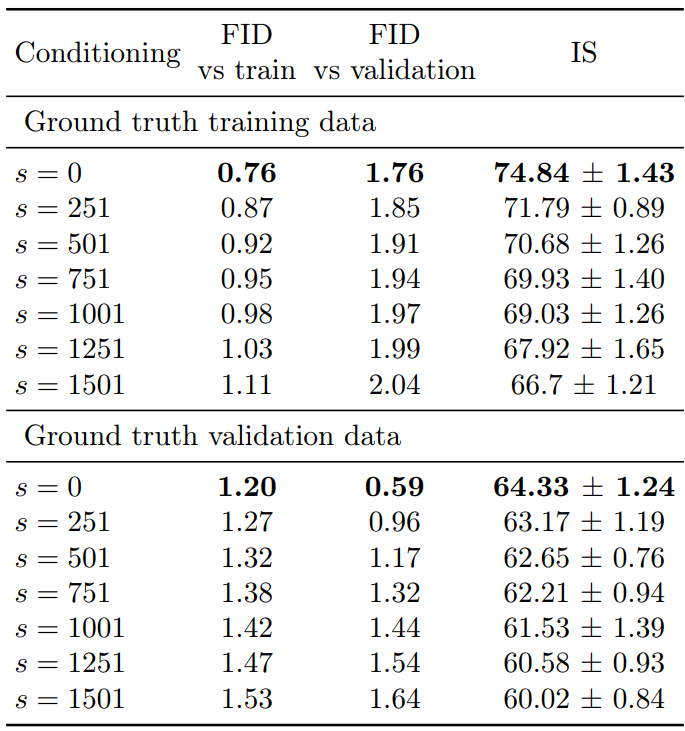
다음 표는 super-resolution 모델에 생성 데이터 대신 ground truth 데이터를 조건으로 주었을 때의 결과이다.

4. Experiments at 128×128 and 256×256

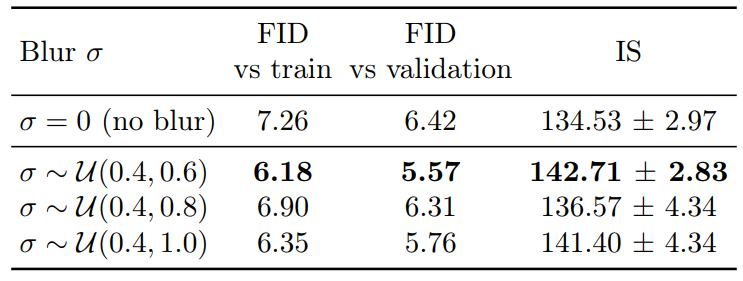
다음은 64$\times$64 → 256$\times$256 super-resolution 모델에 Gaussian blur augmentation을 적용한 결과이다.

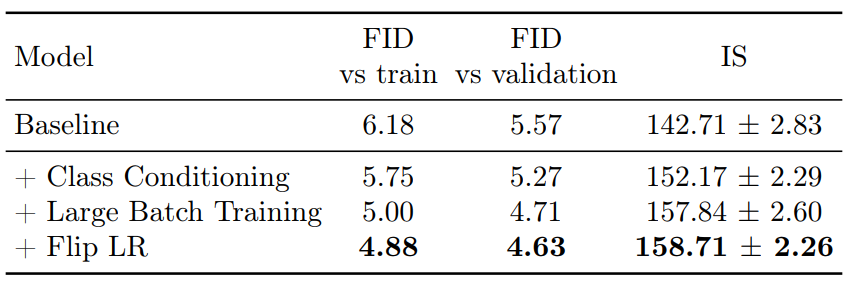
다음은 class conditioning, large batch training, random flip augmentation로 super-resolution 모델을 개선한 결과이다.

5. Experiments on LSUN

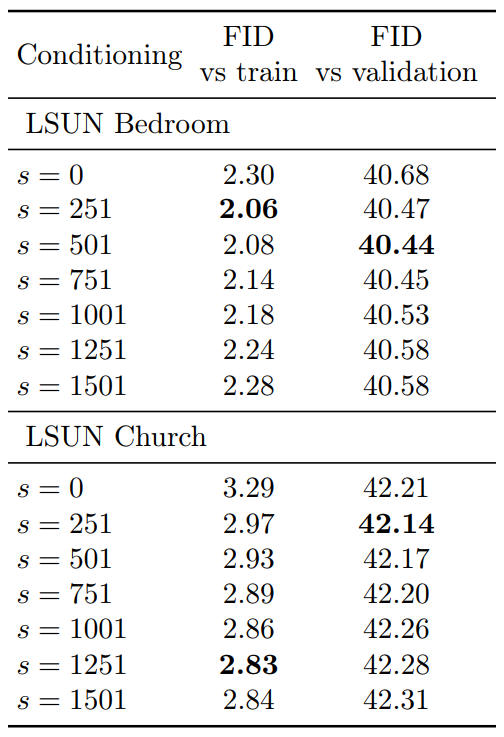
다음은 128$\times$128 LSUN에서의 샘플 품질이다. Non-truncated conditioning augmentation을 64$\times$64 → 128$\times$128 계단식 파이프라인에 사용하였다.