Blogs

arXiv 2022. [Paper]
Zhendong Wang, Huangjie Zheng, Pengcheng He, Weizhu Chen, Mingyuan Zhou
The University of Texas at Austin | Microsoft Azure AI
11 Oct 2022

Introduction

GAN과 GAN의 변형 모델들은 사실적인 고해상도 이미지 합성에 큰 성과를 거두었다. 하지마 실제로 GAN은 수렴하지 않거나 학습이 불안정하며 mode collapse가 발생하는 등의 다양한 문제를 겪는다.

GAN 학습을 안정화하는 간단한 방법은 instance noise를 주입하는 것이다. 즉, discriminator의 입력에 noise를 추가하여 generator와 discriminator 분포 모두의 지원을 확대하고 discriminator가 overfitting되는 것을 방지할 수 있다. 하지만 이 방법은 적합한 noise 분포를 찾는 것이 어렵기 때문에 실제로 사용하기 힘들다.

Roth et al. (2017)은 고차원 discriminator의 입력에 instance nosie를 더하는 것이 잘 작동하지 않음을 보였으며, zero-centered gradient penalty를 discriminator에 더하여 이를 근사화하는 것을 제안하였다. Mescheder et al. (2018)은 이 방법이 이론적으로나 실험적으로 수렴하는 것을 보였으며, 학습이 안정되어 WGAN-GP보다 더 성능이 좋다는 것을 보였다. 하지만 Brock et al. (2018)은 zero-centered gradient penalty나 다른 비슷한 정규화 방법이 성능을 대가로 학습을 안정화한다고 경고했다. 어떤 기존 연구도 고해상도 이미지에서 instance noise를 GAN 학습에 사용하는 것을 성공하지 못하였다.

본 논문은 GAN 학습에 적합한 instance noise를 주입하기 하기 위하여 Diffusion-GAN을 제안한다. Diffusion-GAN은 diffusion process를 사용하여 Gaussian-mixture distributed instance noise를 생성한다. Diffusion-GAN의 구조는 다음과 같다.

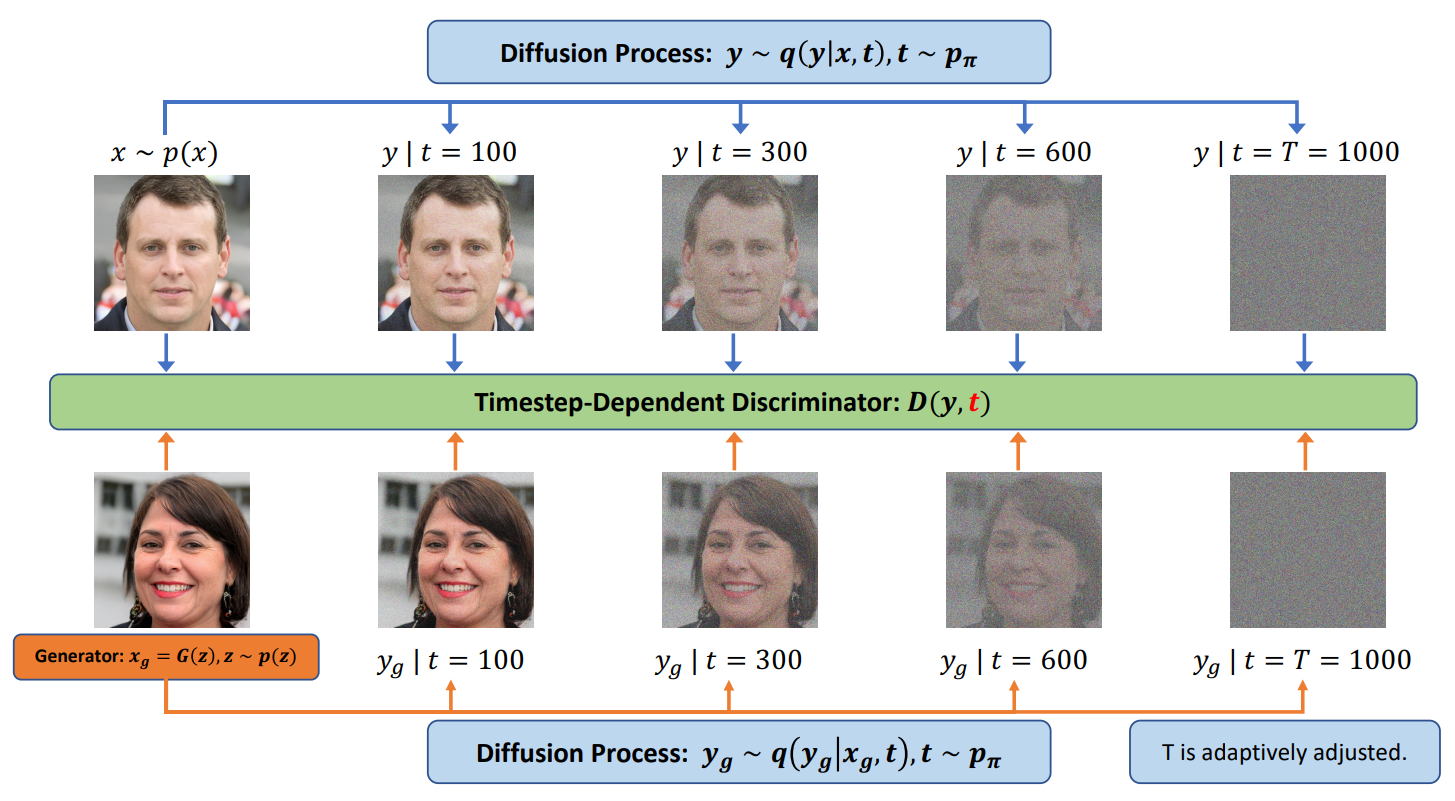
Diffusion process은 실제 이미지나 생성된 이미지가 입력으로 주어지며, 점진적으로 이미지에 noise를 추가하는 일련의 step으로 이루어져 있다. Step의 수는 고정되지 않고 데이터나 generator에 의존한다. 저자들은 diffusion process가 미분 가능하도록 설계하여 input에 대한 output의 미분 값을 계산할 수 있게 한다. 이를 통해 discriminator의 기울기를 diffusion process를 통해 generator로 전파하고, generator를 업데이트할 수 있게 된다. 기존 GAN이 실제 이미지와 생성된 이미지를 바로 비교하지만, Diffusion-GAN은 diffusion process로 noise가 추가된 이미지들을 비교한다. 이 noise 분포는 step마다 서로 다른 noise-to-data ratio를 가진다. 이에 따른 2가지 이점이 있다.

1. 데이터와 generator의 분포가 너무 다른 경우 발생하는 vanishing gradient 문제를 완화하여 학습을 안정시킨다.
2. 같은 이미지라도 다양하게 noise를 추가할 수 있으므로 data augmentation 효과가 있고, 이는 데이터의 효율성과 generator의 다양성을 개선한다.

본 논문은 이 방법의 타당성을 이론적으로 분석하며, 데이터와 generator의 분포의 차이를 측정하는 Diffusion-GAN의 목적 함수가 모든 곳에서 연속적이며 미분 가능함을 보인다. 이는 이론적으로 generator가 언제나 discriminator에서 유용한 gradient를 받을 수 있음을 의미하며, 이는 성능 개선으로 이어진다.

본 논문의 기여를 정리하면 다음과 같다.

1. Diffusion process가 미분 가능한 augmentation을 제공하여 데이터의 효율성과 학습의 안정성을 개선한다.
2. 광범위한 실험으로 Diffusion-Gan이 안정성과 생성 성능을 향상시키는 것을 보였다.

Preliminaries: GANs and diffusion-based generative models

GAN은 generator와 discriminator의 min-max game을 통해 데이터 분포 $p(x)$를 학습하는 것이 목표이다. Generator $G$는 random noise $z$를 입력받아 데이터와 유사한 사실적인 샘플 $G(z)$를 생성하는 것을 시도한다. Discriminator $D$는 실제 데이터 $x \sim p(x)$와 가짜 샘플 $G(z)$를 입력받아 진짜인지 가짜인지 분류한다. GAN의 min-max 목적함수는 다음과 같다.

\[\begin{equation} \min_G \max_D V(G, D) = \mathbb{E}_{x \sim p(x)} [\log (D(x))] + \mathbb{E}_{z \sim p(z)} [\log (1-D(G(z)))] \end{equation}\]

Diffusion-based generative model은 데이터 $x_0 \sim p(x_0)$와 같은 크기의 latent variable $x_1, \cdots, x_T$에 대하여

\[\begin{equation} p_\theta (x_0) := \int p_\theta (x_{0:T}) dx_{1:T} \end{equation}\]

라 가정한다. Forward diffusion chain은 미리 정의된 $\beta_t$와 $\sigma$에 따라 $T$ step에 걸쳐 점진적으로 noise를 $x_0$에 추가한다.

\[\begin{equation} q(x_{1:T} \vert x_0) := \prod_{t=1}^T q(x_t | x_{t-1}), \quad \quad q(x_t | x_{t-1}) := \mathcal{N} (x_t; \sqrt{1-\beta_t} x_{t-1}, \beta_t \sigma^2 I) \end{equation}\]

또한 다음과 같이 closed form으로 임의의 timestep $t$에서 $x_t$를 샘플링할 수 있다.

\[\begin{equation} q(x_t | x_0) = \mathcal{N}(x_t ; \sqrt{\vphantom{1} \bar{\alpha}_t} x_0, (1-\bar{\alpha}_t) \sigma^2 I), \quad \quad \textrm{where} \quad \alpha_t := 1- \beta_t, \; \bar{\alpha}_t := \prod_{s=1}^t \alpha_s \end{equation}\]

Reverse diffusion chain은 다음과 같다.

\[\begin{equation} p_\theta (x_{0:T}) := \mathcal{N} (x_T ; 0, \sigma^2 I) \prod_{t=1}^T p_\theta (x_{t-1} | x_t) \end{equation}\]

Diffusion-GAN: Method and Theoretical Analysis

1. Instance noise injection via diffusion

Latent variable $z$를 고차원 데이터 space로 매핑하는 Generator $G$가 사실적인 샘플 $x_g$를 생성하는 것이 목표이다. Generator를 robust하고 diverse하게 만들기 위해서는 $x_g$에 instance noise를 주입해야 한다. Diffusion step은 원본 이미지 $x$에서 시작해서 점진적으로 정보를 지워 $T$ step 후 noise level $\sigma^2$에 도달하는 Markov chain으로 볼 수 있다.

혼합 분포 $q(y \vert x)$를 모든 step에서 얻은 noise가 추가된 샘플 $y$의 가중치 합이라고 정의하자. 이 때 각 step $t$에서의 가중치는 $\pi_t$이다. 특정 step $t$에서의 component $q(y \vert x, t)$는 평균이 $x$에 비례하고 분산이 step $t$에 의존한다. 실제 데이터 $x \sim p(x)$와 생성된 샘플 $x_g \sim p_g(x)$의 혼합 분포는 같은 diffusion process로 구한다. 수식으로 정리하면 다음과 같다.

\[\begin{equation} x \sim p(x), y \sim q(y | x), \quad q(y | x) := \sum_{t=1}^T \pi_t q(y | x, t) \\ x_g \sim p_g(x), y_g \sim q(y_g | x_g), \quad q(y_g | x_g) := \sum_{t=1}^T \pi_t q(y_g | x_g, t) \end{equation}\]

$q(y \vert x)$는 $T$개의 component로 이루어진 혼합 분포이며, 가중치 $\pi_t$는 음이 아닌 실수이며 모두 더하면 1이다. Component $q(y \vert x, t)$는 다음과 같이 diffusion process로 계산된다.

\[\begin{equation} q(y | x, t) = \mathcal{N} (y; \sqrt{\vphantom{1} \bar{\alpha_t}}x , (1-\bar{\alpha}_t) \sigma^2 I) \end{equation}\]

혼합 분포에서의 샘플링은

\[\begin{equation} t \sim p_\pi := \textrm{Discrete}(\pi_1, \cdots, \pi_T), \quad \quad y \sim q(y \vert x, t) \end{equation}\]

으로 진행된다. 혼합 분포에서 $y$를 샘플링하여 실제 이미지와 생성된 이미지 모두에 대한 다양한 정도의 noise가 추가된 이미지를 얻을 수 있다. 더 많은 noise가 추가될 수록 $x$의 정보는 적어진다.

2. Adversarial Training

Diffusion-GAN은 다음 min-max game 목적 함수를 풀어 generator와 discriminator를 학습한다.

\[\begin{equation} V(G, D) = \mathbb{E}_{x \sim p(x), t \sim p_\pi, y \sim q(y \vert x, t)} [\log (D_\phi (y, t))] + \mathbb{E}_{z \sim p(z), t \sim p_\pi, y_g \sim q(y_g \vert G_\theta (z), t)} [\log (1 - D_\phi (y_g, t))] \end{equation}\]

목적 함수는 discriminator가 모든 diffusion step $t$에 대하여 교란된 실제 데이터에는 높은 확률을, 교란된 생성된 데이터에는 낮은 확률을 부여하도록 한다. 반면 generator는 모든 $t$에서 discriminator를 속일 수 있는 샘플을 생성하려고 시도한다. 교란된 데이터는 reparameterization을 이용하여 다음과 같이 계산할 수 있다.

\[\begin{equation} y = \sqrt{\vphantom{1} \bar{\alpha}_t} x + \sqrt{1 - \bar{\alpha}_t} \sigma \epsilon \quad \quad \epsilon \sim \mathcal{N} (0, I)\\ y_g = \sqrt{\vphantom{1} \bar{\alpha}_t} G_\theta (z) + \sqrt{1 - \bar{\alpha}_t} \sigma \epsilon \quad \quad \epsilon \sim \mathcal{N} (0, I) \end{equation}\]

Reparameterization으로 계산을 하면 목적 함수가 generator의 파라미터에 대하여 미분 가능해지므로 역전파로 파라미터를 최적화할 수 있다.

목적 함수는 실제 분포와 생성된 분포 사이의 Jensen–Shannon divergence의 근사

\[\begin{equation} \mathcal{D}_{\textrm{JS}} (p(y, t) \| p_g (y,t)) = \mathbb{E}_{t \sim p_\pi} [\mathcal{D}_{JS} (p(y | t) \| p_g (y | t))] \end{equation}\]

를 최소화할 수 있다. JS divergence는 두 분포가 유사하지 않은 정도를 측정하며, 두 분포가 동일하면 값이 0이 된다.

두 교란된 분포 사이의 JS divergence를 최소화하는 최적의 generator가 원래 분포 사이의 JS divergence를 최소화하는 최적의 generator이다.

3. Adaptive diffusion

Discriminator $D$는 적당히 어려운 task를 풀어야 한다. 너무 쉬어서 overfitting되지 않아야 하며 너무 어려워서 학습이 방해되어도 안 된다. 따라서 저자들은 $D$가 얼마나 $y$와 $y_g$를 구별할 수 있는 지에 따라 $y$와 $y_g$에 더해지는 noise를 조절한다. $t$가 커지면 noise-to-data ratio가 커져 task가 어려워진다. 따라서 $t$가 커지면 같이 커지는 $1-\bar{\alpha}_t$를 사용하여 diffusion 강도를 측정한다. Diffusion 강도를 조절하기 위하여 최대 step 수 $T$를 적응적으로 수정한다.

이러한 전략은 discriminator가 가장 쉬운 샘플인 원본 데이터 샘플부터 학습하도록 하며, 더 큰 $t$에 대하여 샘플링하여 점진적으로 난이도를 올린다. 이를 위하여 $T$에 대하여 자율 스케줄을 사용하며, 이는 discriminator가 얼마나 overfit되어 있는지를 추정하는 metric $r_d$에 의존한다.

\[\begin{equation} r_d = \mathbb{E}_{y,t \sim p(y, t)} [\textrm{sign} (D_\phi (y, t) - 0.5)], \quad \quad T = T + \textrm{sign} (r_d - d_{target}) \cdot C \end{equation}\]

여기서 $C$는 상수이다. $r_d$는 4개의 minibatch마다 계산되어 $T$를 업데이트한다. $t$를 샘플링하는 $p_\pi$에 대한 2가지 옵션이 있다.

\[\begin{equation} t \sim p_\pi := \begin{cases} \textrm{uniform}: & \textrm{Discrete} (\frac{1}{T}, \frac{1}{T}, \cdots, \frac{1}{T}) \\ \textrm{priority}: & \textrm{Discrete} \bigg(\frac{1}{\sum_{t=1}^T t}, \frac{1}{\sum_{t=1}^T t}, \cdots, \frac{1}{\sum_{t=1}^T t}\bigg) \end{cases} \end{equation}\]

“priority” 옵션은 더 큰 $t$에 더 큰 가중치를 주는 방법으로, $T$가 증가할 때 discriminator가 새로운 샘플을 더 많이 볼 수 있도록 한다. 이는 discriminator가 전에 보지 못한 새롭고 더 어려운 샘플에 더 집중할 수 있도록 하기 위함이다. “priority” 옵션이라도 discriminator 여전히 작은 $t$에 대한 샘플을 볼 수 있다.

갑작스러운 $T$의 변화를 막기 위해 $p_\pi$에서 뽑힌 $t$ 값을 포함하는 탐색 리스트 $t_epl$를 사용한다. $T$가 업데이트되기 전까지 $t_epl$는 고정되며 $t_epl$에서 $t$를 뽑는다. 이 방법을 사용하면 더 큰 $T$로 업데이트되기 전에 각 $t$에 대하여 충분히 탐색할 수 있다.

4. Theoretical analysis with Examples

본 논문에서는 WGAN과 동일한 toy exmaple을 이용하여 Diffusion-GAN을 설명한다. 실제 데이터를 $x = (0, z)$라 하고, 생성된 데이터를 $x_g = (\theta, z)$라 둔다. 생성된 데이터는 1개의 파라미터 $\theta$로 생성되며 $z \sim \mathcal{N} (0, I)$이다.

실제 데이터 분포와 생성된 데이터 분포 사이의 JS divergence $\mathcal{D}_{\textrm{JS}} (p(x) \vert \vert p(x_g))$는 $\theta = 0$일 때만 0이고 $\theta \ne 0$일 때 $\log 2$이다.

다음은 toy exmaple에 diffusion 기반의 noise를 추가한 결과이다.

위는 $t$에 대한 diffusion noise를 주입한 데이터 분포이고, 아래는 JS divergence와 최적의 discriminator 값이다.

$t$가 증가함에 따라 JS divergence 그래프는 더 부드러워지고 더 넓은 $\theta$ 범위에서 기울기가 0이 아니게 된다. $t$가 작을 때는 JS divergence가 거의 상수인 부분이 여전히 존재한다. 이를 피하기 위해서는 모든 step을 혼합하여 의미있는 기울기를 얻을 확률을 항상 높게 유지하여야 한다.

Noise가 없는 JS divergence의 최적의 discriminator 값은 불연속적이다. Diffusion 기반의 noise를 추가하면 $t$에 따라 최적의 discriminator가 바뀐다. 미분 가능한 forward diffusion chain을 사용하면 다양한 수준의 기울기를 제공하여 generator의 학습을 도울 수 있다.

Experiments

다음은 StyleGAN2에 Diffusion-GAN 기법을 추가하여 학습시킨 Diffusion StyleGAN2를 기존 모델들과 비교한 결과이다.

다음은 다양한 데이터셋에서 학습된 Diffusion StyleGAN2이 생성한 샘플들이다.

다음은 학습이 진행됨에 따라 적응적으로 변화하는 $T$와 discriminator의 출력값을 나타낸 그래프이다.

     

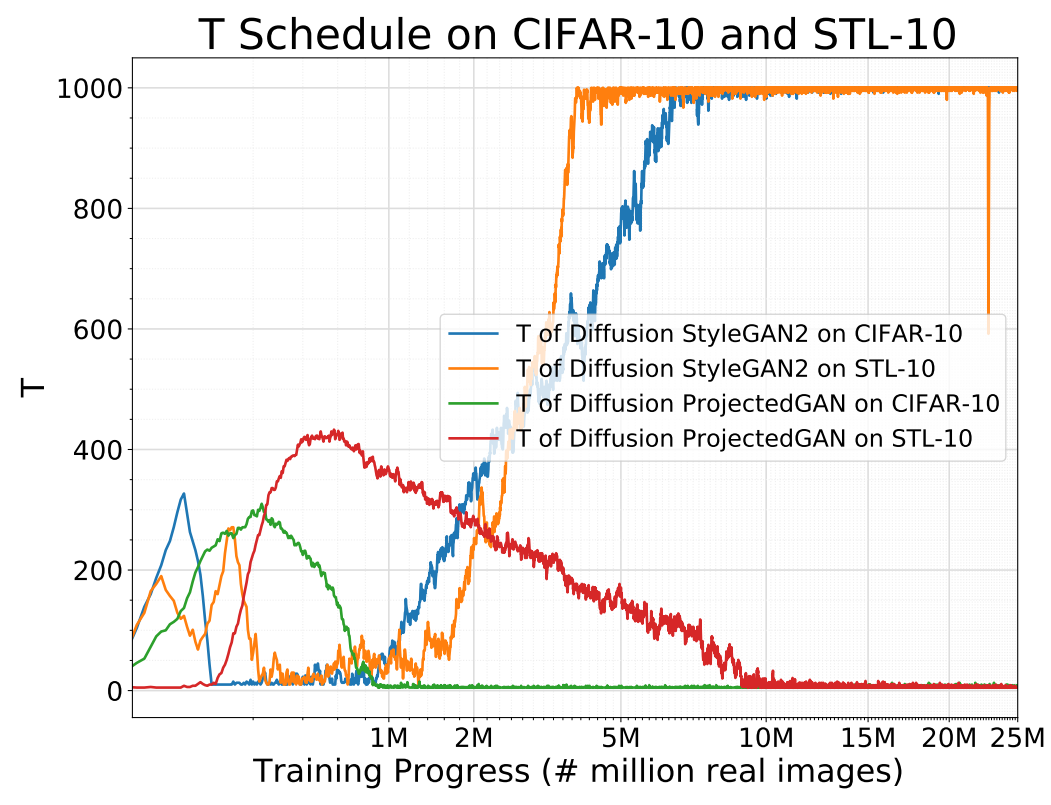
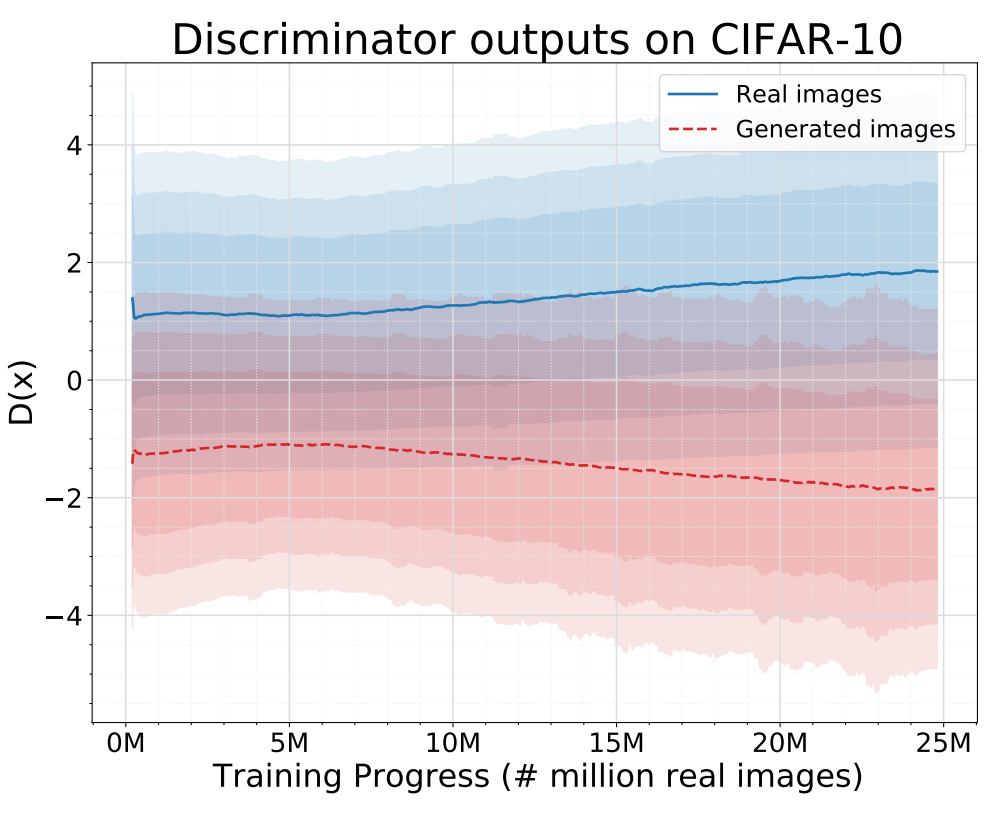
Diffusion 기반의 혼합 분포로 학습된 discriminator가 항상 잘 작동하고 generator에 유용한 학습 신호를 제공한다는 것을 보여준다.

다음은 일반 GAN과 Diffusion-GAN을 25-Gaussians exmaple에 대해 실험한 결과이다.

일반 GAN은 mode collapse가 발생하여 몇몇 모드만 포착하였다. 일반 GAN의 실제 샘플과 생성된 샘플의 discriminator 출력값은 빠르게 멀어진다. 이는 discriminator에 강한 overfitting이 발생한다는 것을 의미하며 discriminator가 generator에 유용한 학습 신호를 제공하는 것을 멈춘다고 볼 수 있다.

반면, Diffusion-GAN은 25개의 모드를 모두 포착하며 discriminator가 지속적으로 유용한 학습 신호를 제공한다. 이러한 결과를 통해 2가지 관점에서 개선점을 해석할 수 있다.

1. Non-leaking augmentation은 데이터 space의 정보를 더 제공한다.
2. Discriminator가 적응적으로 조절되는 diffusion 기반의 noise 주입에 잘 작동한다.

다음은 ProjectGAN과의 Diffusion ProjectGAN의 비교 결과이다.