Blogs

NeurIPS Workshop 2021. [Paper]
Jonathan Ho, Tim Salimans
Google Research, Brain team
28 Sep 2021

Introduction

Diffusion Models Beat GANs on Image Synthesis 논문에서는 추가 classifier를 학습하여 샘플의 품질의 향상시키는 classifier guidance가 제안되었다. Classifier guidance는 diffusion model의 score 추정치와 classifier의 로그 확률의 입력 기울기를 혼합한다. Classifier gradient의 강도를 변경하여 Inception Score (IS)와 FID (또는 precision과 recall)를 절충할 수 있다.

저자들은 classifier 없이 classifier guidance을 수행할 수 있는지 여부에 관심을 가졌다. Classifier guidance는 추가 classifier를 학습시켜야 하기 때문에 diffusion model의 학습 파이프라인을 복잡하게 한다. 또한 이 classifier는 noise가 있는 데이터에 대해 학습시켜야 하므로 pre-trained classifier를 연결할 수 없다.

또한 본 논문은 classifier guidance가 샘플링 중에 score 추정치를 classifier gradient와 혼합하기 때문에 FID나 IS와 같은 classifier-based metric을 의도적으로 향상시키기 위한 gradient-based adversarial attack이라고 문제를 제기한다. Classifier gradient의 방향으로 나아가는 것이 GAN의 학습과 일부 유사하며, GAN은 이미 classifier-based metric에서 좋은 결과를 보이기 때문이다.

저자들은 이 문제를 해결하기 위해 어떠한 classifier도 사용하지 않는 classifier-free guidance를 제안한다. Classifier-free guidance는 이미지 classifier의 기울기 방향으로 샘플링하는 대신 conditional diffusion model과 함께 학습된 unconditional diffusion model의 score 추정치를 혼합한다. 혼합 가중치를 사용하여 classifier guidance에서 얻은 것과 유사한 FID/IS tradeoff를 얻는다. 또한 pure generative diffusion model이 다른 유형의 생성 모델과 함께 매우 높은 fidelity의 샘플을 합성하는 것이 가능하다.

Background

본 논문은 연속적인 시간에서 diffusion model을 학습시킨다. $x \sim p(x)$이고 \(z = \{z_\lambda \vert \lambda \in [\lambda_\textrm{min}, \lambda_\textrm{max}]\}\)라 하자. $\lambda_{\textrm{min}}$과 $\lambda_{\textrm{max}}$는 $\lambda_{\textrm{min}} < \lambda_{\textrm{max}} \in \mathbb{R}$인 hyper-parameter이다. Forward process $q(z \vert x)$는 다음과 같은 variance-preserving Markov process이다.

\[\begin{aligned} q(z_\lambda | x) &= \mathcal{N}(\alpha_\lambda x, \sigma_\lambda^2 I), \quad \quad \textrm{where} \quad \alpha_\lambda^2 = \frac{1}{1+e^{-\lambda}}, \; \sigma_\lambda^2 = 1 - \alpha_\lambda^2 \\ q(z_\lambda | z_{\lambda'}) &= \mathcal{N}\bigg(\frac{\alpha_\lambda}{\alpha_{\lambda'}} z_{\lambda'}, \sigma_{\lambda | \lambda'}^2 I \bigg), \quad \quad \textrm{where} \quad \lambda < \lambda', \; \sigma_{\lambda | \lambda'}^2 = (1 - e^{\lambda - \lambda'}) \sigma_\lambda^2 \end{aligned}\]

$z \sim q(z\vert x)$일 때, $z$(혹은 $z_\lambda$)의 주변 확률 분포를 $p(z)$(혹은 $p(z_\lambda)$)로 표기한다. $\lambda = \log (\alpha_\lambda^2 / \sigma_\lambda^2)$이므로 $\lambda$는 $z_\lambda$의 log signal-to-noise ratio로 생각할 수 있으며, forward process는 $\lambda$가 감소하는 방향으로 진행한다.

$x$를 조건으로 할 때, forward process는

\[\begin{equation} q(z_\lambda' \vert z_\lambda, x) = \mathcal{N}(\tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x), \tilde{\sigma}_{\lambda' \vert \lambda}^2 I) \end{equation}\]

을 reverse하여 나타낼 수 있다. 여기서

\[\begin{equation} \tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x) = e^{\lambda - \lambda'} \bigg(\frac{\alpha_\lambda'}{\alpha_{\lambda}}\bigg) z_{\lambda} + (1 - e^{\lambda - \lambda'}) \alpha_{\lambda'} x, \quad \quad \tilde{\sigma}_{\lambda' \vert \lambda}^2 = (1 - e^{\lambda - \lambda'}) \sigma_{\lambda'}^2 \end{equation}\]

이다. Reverse process는 $p_\theta (z_{\lambda_\textrm{min}}) =\mathcal{N}(0, I)$에서 시작한다. 구체적으로 transition은 다음과 같다.

\[\begin{equation} p_\theta (z_{\lambda'} | z_\lambda) = \mathcal{N} (\tilde{\mu}_{\lambda' \vert \lambda} (z_\lambda, x_\theta (z_\lambda)), (\tilde{\sigma}_{\lambda' \vert \lambda}^2)^{1-v}(\sigma_{\lambda \vert \lambda'}^2)^v) \end{equation}\]

샘플링 중에는 timestep $T$에 대하여 증가수열 $\lambda_\textrm{min} = \lambda_1 < \cdots < \lambda_T = \lambda_\textrm{max}$에 따라 위의 transition이 적용된다. 만일 모델 $x_\theta$가 정확하다면 $T$가 무한대로 갈 때 샘플 경로가 $p(z)$로 분포된 SDE에서 샘플을 얻을 수 있으며, 모델의 분포를 $p_\theta (z)$로 표기한다.

분산은 Improved DDPM에서 사용한 것처럼 \(\tilde{\sigma}_{\lambda' \vert \lambda}^2\)와 \(\tilde{\sigma}_{\lambda \vert \lambda'}^2\)의 log-space interpolation이며, $v$는 Improved DDPM 논문과는 다르게 hyper-parameter를 사욯하는 것이 효과적이라고 한다.

Reverse process의 평균은 \(q(z_{\lambda'} \vert z_\lambda, x)\)에 연결된 추정치 $x_\theta (z_\lambda)$에서 온다. $x_\theta$도 $\lambda$를 입력으로 받지만 깔끔한 표기를 위해 생략한다. DDPM 논문과 동일하게 $x_\theta$를

\[\begin{equation} x_\theta (z_\lambda) = \frac{z_\lambda - \sigma_\lambda \epsilon_\theta (z_\lambda)}{\alpha_\lambda} \end{equation}\]

로 parameterize하며, 목적 함수

\[\begin{equation} \mathbb{E}_{\epsilon, \lambda} \bigg[ \| \epsilon_\theta (z_\lambda) - \epsilon \|_2^2 \bigg] \end{equation}\]

로 학습시킨다. 여기서 $\epsilon \sim \mathcal{N} (0,I)$이고 $z_\lambda = \alpha_\lambda x + \sigma_\lambda \epsilon$이다. $\lambda$는 $[\lambda_\textrm{min}, \lambda_\textrm{max}]$에 대한 분포 $p(\lambda)$에서 뽑는다.

본 논문에서는 $\lambda$를

\[\begin{equation} \lambda = -2 \log \tan (au+b), \quad \quad \textrm{where} \quad b = \arctan (e^{-\lambda_\textrm{max}/2}), \; a = \arctan (e^{-\lambda_\textrm{min}/2}) - b \end{equation}\]

로 뽑으며, $u \in [0, 1]$은 uniform하게 분포한다. 이는 제한된 interval에서 사용할 수 있는 수정된 hyperbolic secant 분포이다.

유한한 수의 timestep으로 생성하는 경우, $\lambda$를 균일한 간격의 $u \in [0, 1]$에 해당하는 값을 사용하고 최종 생성된 샘플은 $x_\theta (z_{\lambda_\textrm{max}})$이다.

$\epsilon_\theta (z_\lambda)$를 위한 loss가 모든 $\lambda$를 위한 denoising score matching이기 때문에, score $\epsilon_\theta (z_\lambda)$는 noise가 있는 데이터 $z_\lambda$ 분포의 log-density의 기울기, 즉

\[\begin{equation} \epsilon_\theta (z_\lambda) \approx -\sigma_\lambda \nabla_{z_\lambda} \log p(z_\lambda) \end{equation}\]

를 추정한다. 그러나 제약이 없는 신경망을 사용하여 $\epsilon_\theta$를 정의하기 때문에 기울기가 $\epsilon_\theta$인 scalar potential은 필요없다. 샘플링은 Langevin diffusion을 사용하여 원본 데이터 $x$의 조건부 분포 $p(x)$로 수렴하는 일련의 분포 $p(z_\lambda)$에서 샘플링하는 것과 유사하다.

조건부 생성의 경우, $x$는 컨디셔닝 정보 $c$와 함께 주어진다. 바뀌는 점은 $\epsilon_\theta$가 $\epsilon_\theta (z_\lambda, c)$와 같이 $c$를 입력으로 받는 것 뿐이다.

Guidance

GAN이나 flow-based model의 경우, 샘플링 시에 분산이나 입력 noise의 범위를 줄여 truncated sampling이나 low temperature sampling을 수행한다. 이런 방법들은 샘플의 다양성을 줄이면서 각 샘플의 품질을 높인다. 하지만, diffusion model의 경우 이러한 방법들이 효과적이지 않다.

1. Classifier guidance

(자세한 내용은 Paper review 참고)

Truncated sampling과 비슷한 효과를 diffusion model에서 얻기 위해 Diffusion models beat GANs on image synthesis 논문은 classifier guidance를 제안하였다. Classifier 모델 $p_\theta (c \vert z_\lambda)$의 log-likelihood의 기울기를 diffusion score $\epsilon_\theta (z_\lambda , c)$에 다음과 같이 추가한다.

\[\begin{equation} \tilde{\epsilon}_\theta (z_\lambda, c) = \epsilon_\theta (z_\lambda, c) - w \sigma_\lambda \nabla_{z_\lambda} \log p_\theta (c | z_\lambda) \approx - \sigma_\lambda \nabla_{z_\lambda} [\log p(z_\lambda | c) + w \log p_\theta (c | z_\lambda)] \end{equation}\]

여기서 $w$는 classifier guidance의 강도를 조절하는 파라미터이다. 샘플링을 할 떄 \(\epsilon_\theta (z_\lambda, c)\) 대신 \(\tilde{\epsilon}_\theta (z_\lambda, c)\)를 사용하며, 이는 결과적으로

\[\begin{equation} \tilde{p}_\theta (z_\lambda | c) \propto p_\theta (z_\lambda | c) p_\theta (c | z_\lambda)^w \end{equation}\]

에서 샘플을 뽑는 것과 동일하다. 이를 통해 classifier가 알맞은 레이블에 높은 likelihood를 할당하도록 가중치를 높게 조정하며, $w > 0$으로 설정하면 다양성이 감소하지만 IS가 개선된다.

위 그림은 클래스가 3개인 toy 2D 샘플에 대한 guidance의 효과이다. 왼쪽에서 오른쪽으로 갈수록 guidance의 강도가 세진다.

Unconditional model에 가중치 $w+1$로 classifier guidance를 적용하면 이론적으로 가중치 $w$로 conditional model에 적용하는 것과 동일한 결과가 나타난다.

\[\begin{aligned} \epsilon_\theta (z_\lambda) - (w+1) \sigma_\lambda \nabla_{z_\lambda} \log p_\theta (c | z_\lambda) & \approx -\sigma_\lambda \nabla_{z_\lambda} [\log p(z_\lambda) + (w+1)\log p_\theta (c | z_\lambda)] \\ &= -\sigma_\lambda \nabla_{z_\lambda} [\log p(z_\lambda) p_\theta (c | z_\lambda) + w \log p_\theta (c | z_\lambda)] \\ &= -\sigma_\lambda \nabla_{z_\lambda} [\log p(z_\lambda | c) + w \log p_\theta (c | z_\lambda)] \end{aligned}\]

하지만 Diffusion models beat GANs on image synthesis 논문에서는 unconditional model에 classifier guidance를 적용했을 때가 아닌 class-conditional model에 적용했을 때 가장 좋은 결과가 나왔다. 이런 이유로 본 논문은 conditional model을 guide한다.

2. Classifier-Free Guidance

Classifier-free guidance는 $\epsilon_\theta (z_\lambda, c)$를 수정하여 classifier 없이 classifier guidance와 같은 효과를 얻는 방법이다.

다음은 classifier-free guidance의 자세한 학습 알고리즘과 샘플링 알고리즘이다.

별도의 classifier를 학습시키는 대신 $\epsilon_\theta (z_\lambda)$로 parameterize된 unconditional model $p_\theta(z)$와 $\epsilon_\theta (z_\lambda, c)$로 parameterize된 conditional model $p_\theta(z \vert c)$를 함께 학습시킨다. 두 모델을 따로 두지 않고 하나의 모델을 사용하며 unconditional model의 경우 null token $\varnothing$을 조건 $c$로 준다. 즉, $\epsilon_\theta (z_\lambda) = \epsilon_\theta (z_\lambda, c = \varnothing)$이다. 학습 시에는 $p_\textrm{uncond}$의 확률로 $c$가 $\varnothing$이 된다.

샘플링은 다음과 같이 conditional score와 unconditional score의 선형결합으로 진행한다.

\[\begin{equation} \tilde{\epsilon}_\theta (z_\lambda, c) = (1 + w) \epsilon_\theta (z_\lambda, c) - w \epsilon_\theta (z_\lambda) \end{equation}\]

위 식에는 classifier gradient가 없으므로 \(\tilde{\epsilon}_\theta\)의 방향으로 가는 것이 gradient-based adversarial attack이라고 볼 수 없다. 또한, \(\tilde{\epsilon}_\theta\)는 제한되지 않은 신경망을 사용하기 때문에 비보존적 벡터장인 score 추정치로부터 구성되므로 일반적으로 \(\tilde{\epsilon}_\theta\)가 classifier-guided score인 scalar potential이 존재할 수 없다.

Classifier-guided score가 위 식과 같은 classifier가 존재하지 않을 수 있지만, 위 식은 실제로 implicit classifier $p^i (c \vert z_\lambda) \propto p (z_\lambda \vert c) / p(z_\lambda)$의 gradient에서 영감을 받았다. 만일 정확한 score $\epsilon^\ast (z_\lambda, c)$와 $\epsilon^\ast (z_\lambda)$를 안다면, implicit classifier의 기울기는

\[\begin{equation} \nabla_{z_\lambda} \log p^i (c | z_\lambda) = -\frac{1}{\sigma_\lambda} [\epsilon^\ast (z_\lambda, c) - \epsilon^\ast (z_\lambda)] \end{equation}\]

가 되며, score 추정치는

\[\begin{equation} \tilde{\epsilon}^\ast (z_\lambda, c) = (1 + w) \epsilon^\ast (z_\lambda, c) - w \epsilon^\ast (z_\lambda) \end{equation}\]

로 수정된다. $\tilde{\epsilon}^\ast (z_\lambda, c)$는 \(\tilde{\epsilon}_\theta (z_\lambda, c)\)와 근본적으로 다르다. $\tilde{\epsilon}^\ast (z_\lambda, c)$는 scaled classifier gradient $\epsilon^\ast (z_\lambda, c) - \epsilon^\ast (z_\lambda)$로부터 구성된 것이고. \(\tilde{\epsilon}_\theta (z_\lambda, c)\)는 score 추정치 $\epsilon_\theta (z_\lambda, c) - \epsilon_\theta (z_\lambda)$로 구성된 것이며 어떤 classifier의 기울기도 아니기 때문이다. (Score 추정치는 단순히 신경망의 출력이므로)

베이즈 정리를 사용하여 생성 모델을 뒤집는 것이 유용한 guidance 신호를 제공하는 좋은 classifier를 생성한다는 것은 명백하지 않다. 예를 들어, 생성 모델이 데이터 분포와 정확히 일치하는 인위적인 경우에도 discriminative model들이 일반적으로 생성 모델에서 파생된 implicit classifier들보다 성능이 우수하다. 모델이 데이터 분포와 정확히 일치하지 않는 본 논문의 경우와 같이 베이즈 정리에 의해 파생된 classifier들은 일관성이 없을 수 있으며 성능에 대한 모든 보장을 잃게 된다.

그럼에도 불구하고 Experiments에서는 classifier-free guidance가 classifier guidance와 동일한 방식으로 FID와 IS를 절충할 수 있음을 경험적으로 보여준다. Discussion에서는 classifier-guidance와 관련하여 classifier-free guidance의 의미에 대해 논의한다.

Experiments

본 논문은 단순히 샘플의 품질을 state-of-the-art에 올리는 것에 집중하지 않았으며, classifier-free guidance가 classifier guidance와 비슷하게 FID/IS tradeoff를 달성할 수 있는 지 보이고 classifier-free guidance를 이해하는 것을 목표로 한다.

따라서 저자들은 Diffusion models beat GANs on image synthesis 논문의 guided diffusion model과 동일한 아키텍처와 hyper-parameter를 사용한다. Hyper-parameter가 classifier guidance에 적합하게 세팅되어 있고 classifier-free guidance에는 최적이 아닐 수도 있지만 그대로 사용한다. 또한, conditional model과 unconditional model을 하나의 모델로 구현하였기 때문에 model capacity가 더 작을 것이다. 그럼에도 불구하고 classifier-free guided model은 여전히 경쟁력 있는 품질의 샘플을 생성하며 때때로 더 좋은 성능을 보인다.

모든 모델은 $\lambda_\textrm{min} = -20$과 $\lambda_\textrm{max} = 20$으로 학습되었으며, FID와 IS 계산에 각각 5만개의 샘플들이 사용되었다. 64$\times$64 모델은 $v = 0.3$으로 40만 step만큼 학습되었으며, 128$\times$128 모델은 $v = 0.2$로 270만 step만큼 학습되었다.

다음은 64$\times$64 ImageNet model에서 guidance 강도 $w$가 샘플의 품질에 주는 영향을 보여주는 표와 그래프이다. $p_\textrm{uncond}$를 0.1, 0.2, 0.5로 다르게 하여 실험을 진행하였다.

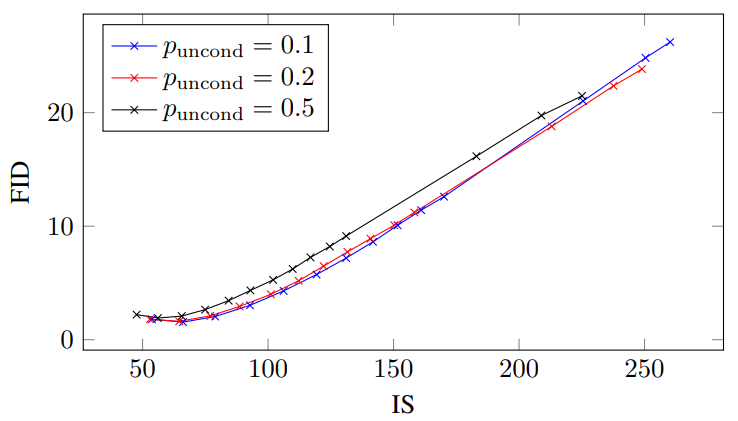
$p_\textrm{uncond}$가 0.5일 때보다 0.1이나 0.2일 때 성능이 더 좋았으며, 0.1과 0.2는 성능이 비슷하였다.

이러한 결과를 바탕으로 샘플의 품질에 효과적인 score를 생성하기 위해서는 diffusion model의 model capacity 중 상대적으로 작은 부분만이 unconditional한 생성에 할애해야 한다는 것을 알 수 있다. 흥미롭게도 classifier guidance의 경우 작은 classifier가 효과적인 샘플링에 충분하다고 하며, 이는 classifier-free guided model의 결과와 같다.

다음은 128$\times$128 ImageNet model에서 guidance 강도 $w$가 샘플의 품질에 주는 영향을 보여주는 표와 그래프이다. Timestep $T$를 128, 256, 512로 다르게 하여 실험을 진행하였다.

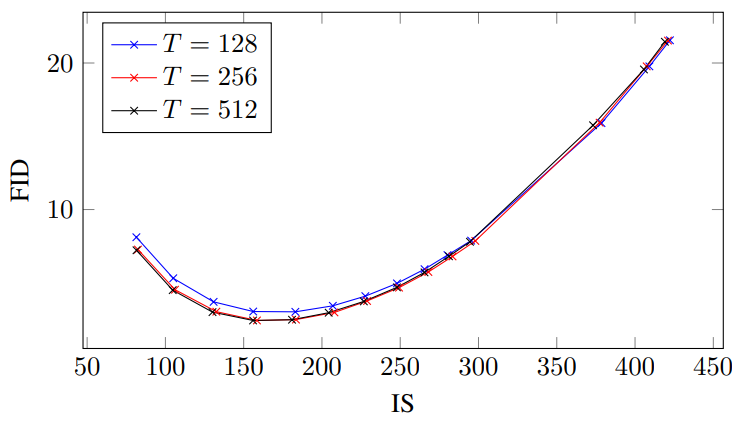
예상한대로 timestep $T$가 클수록 샘플의 품질이 좋았으며 $T = 256$일 때 샘플의 품질과 샘플링 속도가 균형을 이룬다. 특히 $T = 256$일 때 ADM-G 모델(Diffusion models beat GANs on image synthesis)과 샘플링 step의 수가 거의 비슷한 데 본 논문의 모델이 더 성능이 좋다.

두 모델 모두 작은 guidance 강도에서 가장 좋은 FID가 측정되었으며 높은 강도에서 가장 좋은 IS가 측정되었다. 또한 $w$가 증가함에 따라 FID는 감소하고 IS는 증가하였다.

다음은 $w$에 따른 64$\times$64 모델의 샘플링 결과이다.

맨 왼쪽의 샘플들은 guide되지 않은 샘플이며 오른쪽으로 갈수록 guidance 강도가 커진다.

다음은 128$\times$128 모델의 샘플링 결과를 guide되지 않은 샘플과 비교한 것이다.

왼쪽의 샘플들이 guide되지 않은 샘플이며 오른쪽의 샘플들이 $w = 3$으로 classifier-free guide된 샘플이다.

Discussion

Classifier-free guidance의 가장 실용적인 이점은 매우 단순하다는 것이다. Conditional score와 unconditional score의 추정을 혼합하기 위해 학습과 샘플링 중에 코드를 한 줄만 변경하면 된다. 반대로 classifier guidance는 추가로 classifier를 학습시켜야 하므로 학습 파이프라인이 복잡하다. 또한 이 classifier는 noise가 있는 $z_\lambda$에서 학습되어야 하므로 pre-trained classifier를 연결할 수 없다.

Classifier-free guidance는 추가 훈련된 classifier 없이 classifier guidance와 같이 IS와 FID를 절충할 수 있기 때문에 pure generative model로 guide할 수 있음을 입증했다. 또한 diffusion model은 제약 없는 신경망에 의해 parameterize되므로 score 추정치가 classifier gradient와 달리 반드시 보존 벡터장을 형성하지는 않는다. 따라서 classifier-free guided sampler는 classifier gradient와 전혀 유사하지 않은 방향을 따르므로 classifier에 대한 gradient-based adversarial attack으로 해석될 수 없다.

또한 conditional likelihood를 높이면서 샘플의 unconditional likelihood를 줄이는 것으로 guidance가 작동하는 방식에 대한 직관적인 설명이 가능하다. Classifier-free guidance는 본 논문에서 처음 탐구된 음의 score 항으로 unconditional likelihood를 감소시킨다.

제시된 classifier-free guidance는 unconditional model를 학습하는 것에 의존하지만 경우에 따라 이를 피할 수 있다. 클래스 분포가 알려져 있고 소수의 클래스만 있는 경우 $\sum_c(x \vert c)p(c) = p(x)$라는 사실을 사용하여 unconditional score에 대해 명시적으로 학습하지 않고 conditional score에서 unconditional score를 얻을 수 있다. 물론 이것은 가능한 $c$ 값만큼 많은 forward pass가 필요하고 고차원 컨디셔닝에는 비효율적이다.

Classifier-free guidance의 잠재적인 단점은 샘플링 속도이다. 일반적으로 classifier는 생성 모델보다 작고 빠르므로 classifier guidance sampling이 더 빠를 수 있다. 왜냐하면 classifier-free guidance는 diffusion model의 두 가지 forward pass (하나는 conditional score용이고 다른 하나는 unconditional score용)를 실행해야 하기 때문이다. Diffusion model의 여러 pass를 실행해야 하는 필요성은 네트워크 후반에 컨디셔닝을 주입하도록 아키텍처를 변경하여 완화할 수 있다.

마지막으로, 다양성을 희생시키면서 샘플의 품질을 높이는 모든 guidance 방법은 감소된 다양성이 수용 가능한지 생각해보아야 한다. 배포되는 모델에서는 샘플의 다양성을 유지하는 것이 중요하기 때문에 모델에 부정적인 영향이 있을 수 있다. 따라서 샘플의 다양성을 유지하면서 샘플의 품질을 높이는 연구가 필요하다.