Blogs

arXiv 2021. [Paper] [Github]
Robin Rombach, Andreas Blattmann, Dominik Lorenz, Patrick Esser, Björn Ommer
Ludwig Maximilian University of Munich & IWR, Heidelberg University, Germany | Runway ML
20 Dec 2021

Introduction

Diffusion model은 이미지 합성과 super-resolution 분야에서 굉장히 좋은 성능을 보였다. 하지만 데이터의 감지할 수 없는 세부 정보를 모델링하는 데 과도한 자원을 소비하는 경향이 있다. DDPM(논문리뷰)의 재가중된 목적 함수는 초기 노이즈 제거 단계에서 적게 샘플링하여 이 문제를 해결하고자 하지만 이러한 모델을 학습시키고 평가하려면 RGB 이미지의 고차원 공간에서 반복적인 기울기 계산이 필요하기 때문에 여전히 계산적으로 까다롭다. 이러한 모델을 학습시키려면 방대한 컴퓨팅 리소스가 필요하며, 이미 학습된 모델을 평가하기 위해 동일한 모델 아키텍처를 여러 단계에 대해 순차적으로 실행하기 때문에 시간과 메모리가 많이 든다. 강력한 diffusion model에 접근성을 높이고 동시에 상당한 리소스 사용을 줄이려면 학습 및 샘플링 모두에 대한 계산 복잡성을 줄여야 한다. 따라서 diffusion model의 접근성을 높이기 위해서는 성능을 저하시키지 않으면서 계산 요구량을 줄이는 것이 핵심이다.

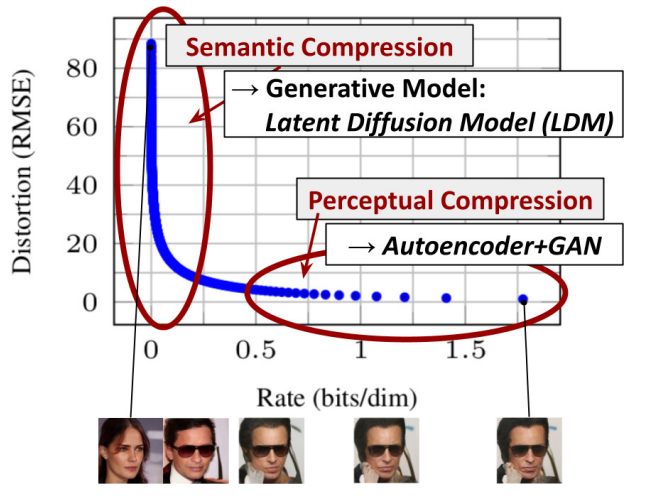
저자들의 접근 방식은 픽셀 공간에서 이미 학습된 diffusion model의 분석으로 시작한다. 위 그림은 학습된 모델의 rate-distortion trade-off를 보여준다. 다른 likelihood 기반 모델과 마찬가지로 학습은 대략 두 단계로 나눌 수 있다.

1. Perceptual compression: high-frequency detail들을 제거하지만 의미(semantic)는 거의 학습하지 않는 단계
2. Semantic compression: 실제 생성 모델이 데이터의 의미론적(semantic) 구성과 개념적(conceptual) 구성을 학습하는 단계

따라서 저자들은 먼저 perceptual하게 동등하지만 계산적으로 더 적합한 space를 찾는 것을 목표로 하며 고해상도 이미지 합성을 위해 diffusion model을 학습시킨다.

먼저, 데이터 space와 perceptual하게 동일한 저차원 representational space로 보내는 autoencoder를 학습한다. 중요한 것은 학습된 잠재 공간에서 diffusion model을 학습시키므로 이전 모델들과 달리 과도한 space 압축에 의존할 필요가 없다는 것이다. 또한 감소된 복잡성으로 인해 네트워크를 한 번만 통과하여 latent space에서 효율적인 이미지 생성이 가능하다. 이 모델을 LDM(Latent Diffusion Models)이라고 한다.

이 접근 방식의 주목할만한 장점은 범용 autoencoding 단계를 한 번만 학습하면 되므로 여러 diffusion model 학습에 재사용하거나 완전히 다른 task를 탐색할 수 있다는 것이다. 이를 통해 다양한 image-to-image 및 text-to-image task를 위한 여러 diffusion model을 효율적으로 탐색할 수 있다. 후자의 경우 트랜스포머를 diffusion model의 UNet backbone에 연결하고 임의의 유형의 토큰으로 조건을 주는 아키텍처를 설계한다.

Method

고해상도 이미지 합성에 대한 diffusion model 학습의 계산 요구량을 낮추기 위해 diffusion model이 해당 손실 항을 적게 샘플링하여 perceptual하게 관련 없는 detail들을 무시할 수 있지만 여전히 픽셀 space에서 계산 비용이 많이 드므로 계산 시간과 컴퓨팅 리소스가 많이 필요하다. 저자들은 학습 단계에서 압축을 명시적으로 분리하여 이러한 단점을 피할 것을 제안한다. 이를 위해 이미지 공간과 perceptual하게 동일한 공간을 학습하지만 계산 복잡성을 크게 줄이는 autoencoding 모델을 활용한다.

이러한 접근은 여러 장점이 있다.

1. 고차원 이미지 space를 남겨두어 저차원 space에서 샘플링이 수행되기 때문에 계산적으로 훨씬 더 효율적이다.
2. UNet 아키텍처에서 상속된 diffusion model의 inductive bias를 활용하여 공간 구조가 있는 데이터에 특히 효과적이다.
3. Latent space가 여러 생성 모델을 훈련하는 데 사용할 수 있고 downstream task (e.g., CLIP-guided synthesis)에도 활용 가능한 범용 압축 모델을 얻는다.

1. Perceptual Image Compression

Perceptual compression 모델은 이전 연구들을 기반으로 하며 perceptual loss와 patch-based adversarial objective의 조합으로 학습되는 autoencoder로 구성된다. 이렇게 하면 local realism이 적용되어 재구성이 image manifold에 국한되고 $L_2$ 또는 $L_1$ objective와 같은 pixel space loss에만 의존하여 발생하는 흐릿함을 방지할 수 있다.

주어진 RGB 이미지 $x \in \mathbb{R}^{H \times W \times 3}$에 대하여 인코더 $\mathcal{E}$가 $x$를 latent representation $z = \mathcal{E}(x)$로 인코딩하고, 디코더 $\mathcal{D}$가 latent $z \in \mathbb{R}^{h \times w \times c}$로부터 이미지를 재구성하여 $\tilde{x} = \mathcal{D}(z) = \mathcal{D}(\mathcal{E}(x))$를 만든다. 인코더는 이미지를 factor $f = H/h = W/w$로 downsample하고 $m \in \mathbb{N}$에 대하여 factor를 $f = 2^m$로 둔다.

저자들은 latent space의 분산이 커지는 것을 막기 위해 두 가지 종류의 정규화로 실험을 진행하였다. 첫 번째 방법인 KL 정규화는 VAE와 유사하게 학습된 latent에서 표준 정규분포에 대해 약간의 KL 페널티를 부과한다. 반면 VQ 정규화는 디코더 내에서 벡터 양자화 layer을 사용한다. 이 모델은 VQGAN으로 해석될 수 있지만 양자화 layer가 디코더에 의해 흡수된다. LDM은 학습된 latent space $z = \mathbb{E}(x)$의 2차원 구조와 함께 작동하도록 설계되었기 때문에 상대적으로 약한 압축률을 사용하고 매우 우수한 재구성이 가능하다. 이는 학습된 space $z$의 임의의 1D 순서에 의존하여 분포를 autoregressive하게 모델링하여 $z$의 고유 구조를 많이 무시한 이전 연구들과 대조된다. 따라서 LDM의 압축 모델은 $x$의 detail들을 더 잘 보존한다. 이는 Experiments의 표에서 확인할 수 있다.

Autoencoder는 patch-based discriminator $D_\psi$로 adversarial 방식으로 학습된다. 높은 수준의 재구성을 위해 매우 작은 크기의 정규화를 사용한다. 예를 들어, KL 항에 대한 가중치를 $10^{-6}$으로 작게 두거나 코드북 차원 $\vert \mathcal{Z} \vert$을 높게 설정한다.

Autoencoding model ($\mathcal{E}$, $\mathcal{D}$)의 전체 목적 함수는 다음과 같다.

\[\begin{equation} L_{\textrm{Autoencoder}} = \min_{\mathcal{E}, \mathcal{D}} \max_{\psi} \bigg( L_{\textrm{rec}} (x, \mathcal{D}(\mathcal{E}(x))) - L_{\textrm{adv}} (\mathcal{D}(\mathcal{E}(x))) + \log D_\psi (x) + L_{\textrm{reg}} (x; \mathcal{E}, \mathcal{D}) \bigg) \end{equation}\]

2. Latent Diffusion Models

Diffusion model은 정규 분포 변수의 noise를 점진적으로 제거하여 데이터 분포 $p(x)$를 학습하도록 설계된 확률 모델이다. 이는 길이가 $T$인 고정된 Markov chain의 reverse process를 학습하는 것이다. 이미지 합성의 경우 가장 성능이 좋은 모델들은 denoising score-matching을 미러링하는 $p(x)$에 대한 variational lower bound를 재가중한 변형을 사용한다. 이러한 모델은 입력 $x_t$의 noise가 제거된 변형을 예측하도록 학습된 denoising autoencoder $\epsilon_\theta (x_t, t) (t = 1, \cdots, T)$의 동등하게 가중된 시퀀스로 해석할 수 있다. 여기서 $x_t$는 입력 $x$에 noise가 추가된 버전이다. 해당 목적 함수는 다음과 같이 단순화할 수 있다.

\[\begin{equation} L_{DM} = \mathbb{E}_{x, \epsilon \sim \mathcal{N} (0,1), t} \bigg[ \| \epsilon - \epsilon_\theta (x_t, t) \|_2^2 \bigg] \end{equation}\]

$t$는 $1, \cdots, T$에서 uniform하게 샘플링된다.

$\mathcal{E}$와 $\mathcal{D}$로 구성된 학습된 perceptual compression 모델을 사용하여 Generative Modeling of Latent Representations을 통해 high-frequency의 감지할 수 없는 detail이 추상화되는 효율적이고 낮은 차원의 latent space에 접근할 수 있다. 이 latent space는 고차원 픽셀 space와 비교할 때 2가지 이유로 likelihood 기반 생성 모델에 더 적합한다.

1. 데이터의 중요한 semantic bit에 집중할 수 있고
2. 계산적으로 훨씬 더 효율적인 더 낮은 차원에서 학습할 수 있기 때문이다.

이전 연구들이 굉장히 압축된 discrete latent space에서 autoregressive attention 기반 transformer 모델에 의존했지만, LDM은 이미지별 inductive bias를 활용할 수 있다. 여기에는 2D convolutional layer들로 UNet을 구성하는 것이 포함되며, 다음과 같은 reweighted bound를 사용하여 perceptual하게 가장 관련성이 높은 비트에 목적 함수를 더 집중시키는 것도 포함된다.

\[\begin{equation} L_{LDM} := \mathbb{E}_{\mathcal{E}(x), \epsilon \sim \mathcal{N}(0,1), t} \bigg[ \| \epsilon - \epsilon_\theta (z_t, t) \|_2^2 \bigg] \end{equation}\]

LDM의 backbone $\epsilon_\theta (\cdot, t)$는 time-conditional UNet으로 구현된다. Forward process가 고정되어 있으므로 학습 중에 $z_t$를 $\mathcal{E}$에서 효율적으로 얻을 수 있고 $p(z)$의 샘플을 $\mathcal{D}$에 한 번 통과시켜 이미지 space로 디코딩할 수 있다.

3. Conditioning Mechanisms

다른 유형의 생성 모델과 마찬가지로 diffusion model은 원칙적으로 $p(z|y)$ 형식의 조건부 분포를 모델링할 수 있다. 이는 조건부 denoising autoencoder $\epsilon_\theta (z_t, t, y)$로 구현되며, 입력 $y$를 통해 텍스트, semantic map, image-to-image 변환과 같은 합성 프로세스를 제어할 수 있다.

그러나 이전 연구들에서는 이미지 합성 측면에서 diffusion model의 생성 능력을 입력 이미지의 클래스 레이블이나 이미지를 흐릿하게 변형하는 것을 넘어선 다른 유형의 컨디셔닝과 결합하는 것은 탐구되지 않았다.

다양한 입력 양식의 attention 기반 모델을 학습하는 데 효과적인 cross-attention 메커니즘으로 기본 UNet backbone을 보강하여 diffusion model을 보다 유연한 조건부 이미지 생성기로 만든다. 다양한 종류의 $y$를 전처리하기 위해 $y$를 중간 representation $\tau_\epsilon (y) \in \mathbb{R}^{M \times d_\tau}$로 보내는 도메인별 인코더 $\tau_\epsilon$를 도입한다. 그런 다음 cross-attention layer를 통해 UNet의 중간 layer에 매핑된다. Cross-attention layer는 다음과 같다.

\[\begin{equation} \textrm{Attention}(Q, K, V) = \textrm{softmax}(\frac{QK^T}{\sqrt{d}}) \cdot V \\ Q = W_Q^{(i)} \cdot \phi_i (z_t), \quad K = W_K^{(i)} \cdot \tau_\theta (y), \quad V = W_V^{(i)} \cdot \tau_\epsilon (y) \end{equation}\]

$\phi_i (z_t) \in \mathbb{R}^{N \times d_\epsilon^i}$는 $\epsilon_\theta$를 구현하는 UNet의 중간 representation이고, $W_V^{(i)} \in \mathbb{R}^{d \times d_\epsilon^i}$, $W_Q^{(i)} \in \mathbb{R}^{d \times d_\tau}$, $W_K^{(i)} \in \mathbb{R}^{d \times d_\tau}$는 학습 가능한 projection matrix이다. 자세한 모델의 아키텍처는 아래와 같다.

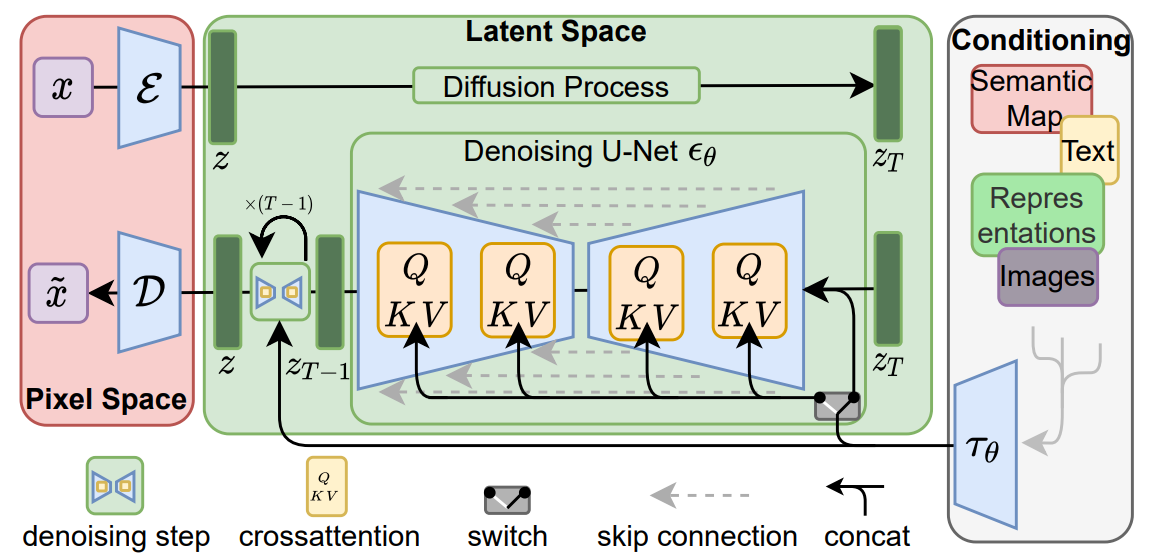
이미지와 conditioning 쌍을 기반으로 다음 식을 통해 조건부 LDM을 학습시킨다.

\[\begin{equation} L_{LDM} := \mathbb{E}_{\mathcal{E} (x), y, \epsilon \sim \mathcal{N} (0, 1), t} \bigg[ \| \epsilon - \epsilon_\theta (z_t, t, \tau_\theta (y)) \|_2^2 \bigg] \end{equation}\]

$\tau_\theta$와 $\epsilon_\theta$는 위 식으로 동시에 최적화된다. 각 도메인별 기존 모델들에 의해 $\tau_\theta$가 파라미터화할 수 있기 떄문에 이 conditioning 메커니즘은 유연하다.

Experiments

먼저 학습 및 inference 모두에서 픽셀 기반 diffusion model과 비교하여 모델의 장점을 분석한다. 흥미롭게도 VQ-regularized latent space에서 학습된 LDM이 때때로 더 나은 샘플 품질을 달성한다. LDM 학습에 대한 정규화 체계의 효과와 $256^2$ 보다 큰 해상도에 대한 재구성 능력 사이의 시각적 비교는 아래 그림과 같다.

1. On Perceptual Compression Tradeoffs

아래 표는 이 섹션에서 비교한 LDM에 사용된 first stage model의 hyper-parameter 및 재구성 성능을 보여준다.

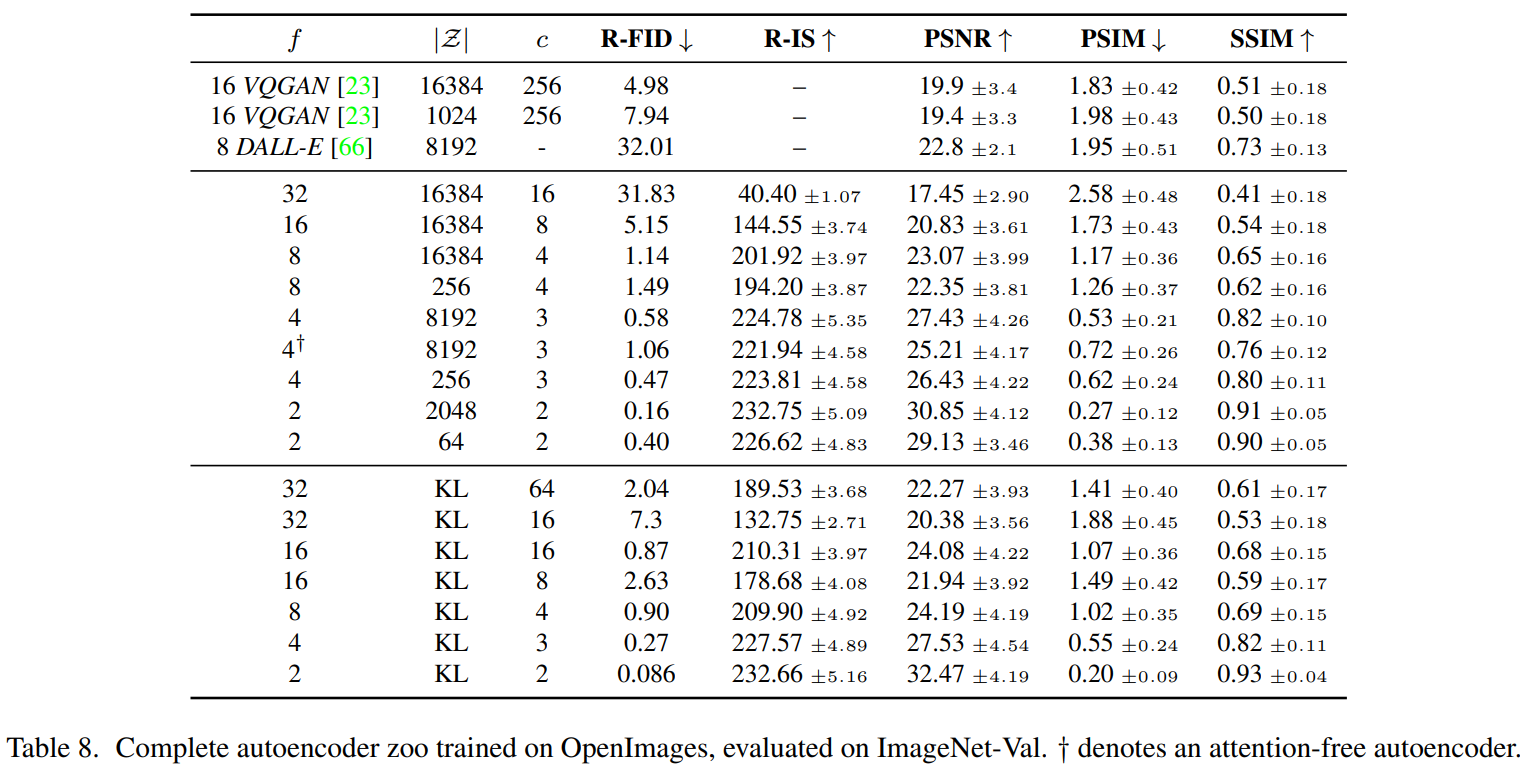
아래 그래프는 ImageNet으로 클래스 조건부 모델을 200만 step 학습할 때 step에 대한 샘플 품질(FID, IS)을 보여준다.
(100 DDIM step으로 샘플링)

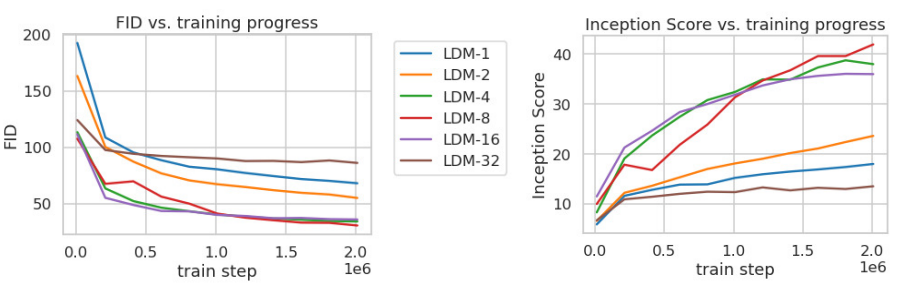
이를 통해 2가지를 확인할 수 있다.

1. 작은 downsampling factor는 학습을 느리게 한다. (LDM-1, LDM-2)
2. 지나치게 큰 f 값은 비교적 적은 step에서 샘플 품질의 정체를 유발한다. (LDM-32)

LDM-4부터 LDM-16까지는 효율성과 perceptual하게 충실한 결과 사이에서 적절한 균형을 유지한다.

아래 그래프는 CelebA-HQ와 ImageNet으로 학습한 LDM의 샘플링 속도와 FID를 비교한 결과이다. CelebA-HQ는 50만 step, ImageNet은 200만 step동안 학습되었으며 각 마커는 10, 20, 50, 100, 200 DDIM step으로 샘플링하였다.

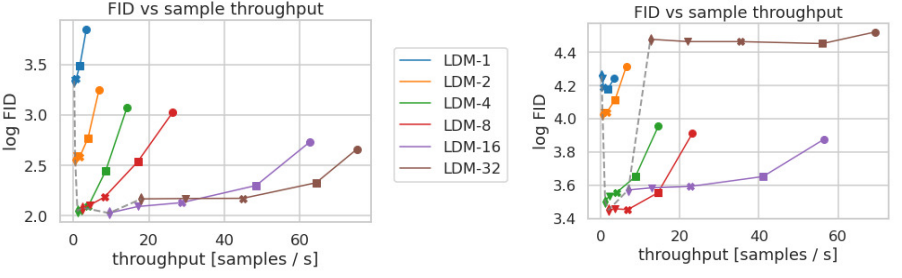
이를 통해 LDM-4와 LDM-8의 성능이 제일 좋다는 것을 알 수 있다.

2. Image Generation with Latent Diffusion

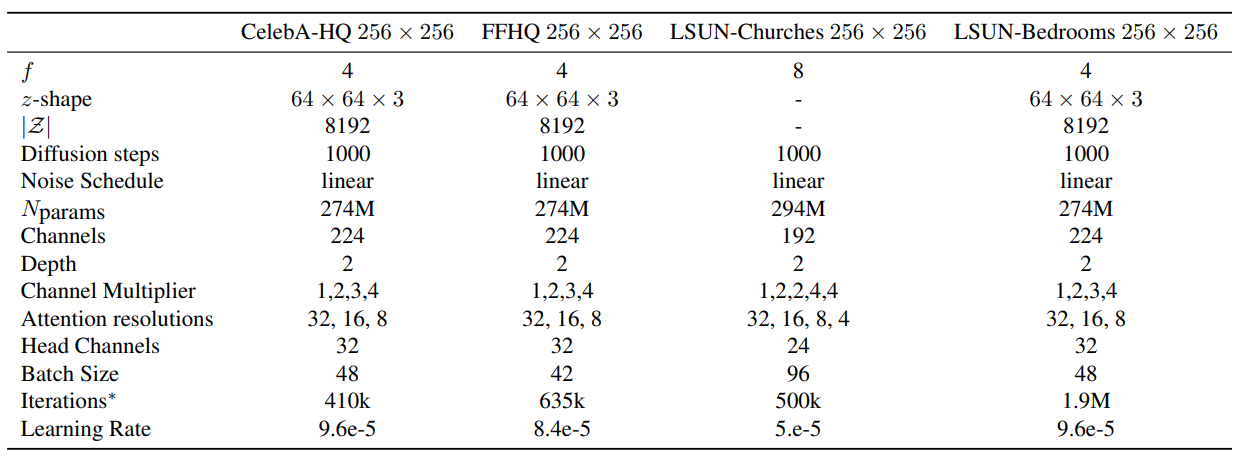
Unconditional LDM의 hyper-parameter는 다음과 같다.

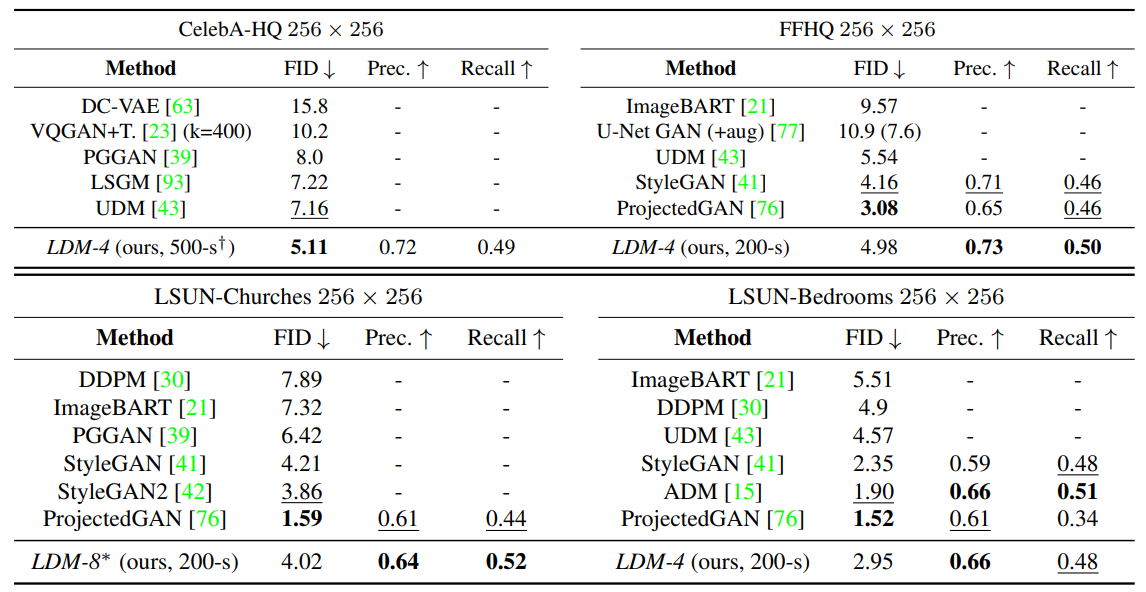
아래 표는 $256^2$ 크기의 CelebA-HQ, FFHQ, LSUN-Churches, LSUN-Bedrooms로 학습한 모델의 FID, Precision, Recall 결과이다.

3. Conditional Latent Diffusion

ImageNet에서 학습한 Conditional LDM의 hyper-parameter는 다음과 같다.

다음은 LAION 데이터셋으로 학습한 LDM-8 (KL)으로 생성한 text-to-image 합성 샘플이다. (200 DDIM step으로 샘플링)

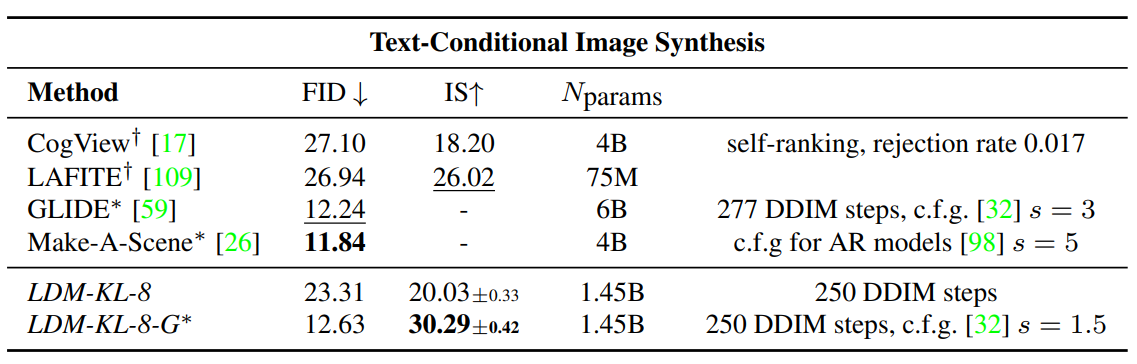
아래 표는 $256^2$ 크기의 MS-COCO 데이터셋으로 text-to-image 합성을 위해 학습된 모델의 결과이다.

다음은 COCO 데이터셋으로 학습한 LDM으로 생성한 layout-to-image 합성 샘플이다.

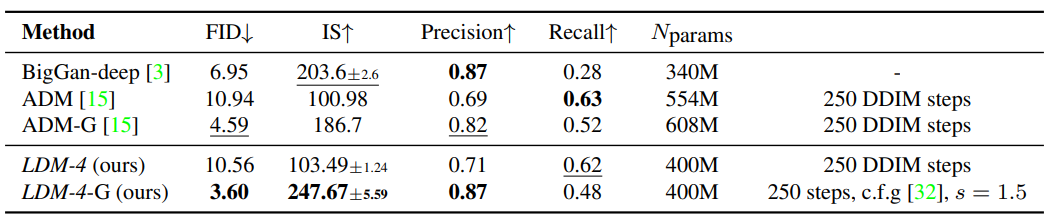
아래 표는 class-conditional ImageNet LDM을 기존 state-of-the-art 모델과 비교한 결과이다.

다음은 풍경 이미지 semantic synthesis를 위해 $256^2$ 크기로 학습한 LDM이 $512 \times 1024$ 크기를 생성하도록 한 결과이다.

4. Super-Resolution with Latent Diffusion

다음은 ImageNet-Val. LDM-SR의 64→256 super-resolution 샘플이다.

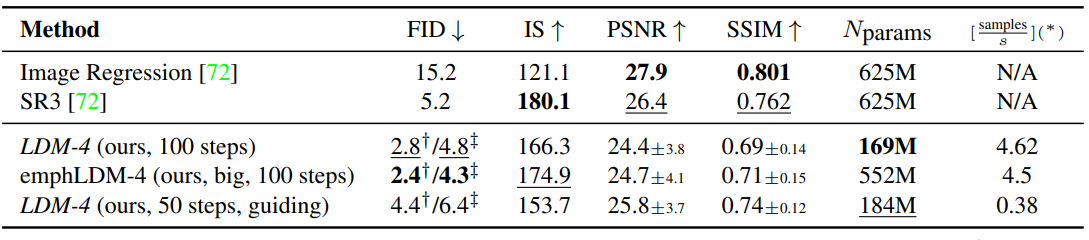
아래 표는 ImageNet-Val.에 대한 64→256 super-resolution 결과이다. (NVIDIA A100 사용)

5. Inpainting with Latent Diffusion

아래 표는 super-resolution과 impainting 성능 비교에 대한 표이다.

다음은 impainting model로 object removal을 진행한 결과이다.

아래 표는 impainting 속도에 대한 표이다.

아래 표는 $512^2$ 크기에서 impainting 성능에 대한 표이다. 40-50% masked는 40%에서 50%가 가려진 샘플에 대한 성능이다.

Limitations

LDM은 픽셀 기반의 방식에 비해 계산 요구량을 크게 줄이지만 샘플링은 여전히 GAN보다 느리다. 또한 높은 정밀도가 필요할 때 LDM을 사용하는 것은 의문의 여지가 있다. $f = 4$ autoencoding model에서는 이미지 품질 손실이 매우 적지만, 픽셀 space에서 세밀한 정확도가 필요한 작업의 경우 재구성 기능이 병목될 수 있다. 저자들은 super-resolution 모델이 이 점에서 이미 어느 정도 제한되어 있다고 생각한다.