Blogs

CVPR 2022. [Paper] [Github]
Doyup Lee, Chiheon Kim, Saehoon Kim, Minsu Cho, Wook-Shin Han
Kakao Brain | POSTECH
3 Mar 2022

Introduction

Vector quantization (VQ)는 autoregressive (AR) 모델의 기본 기술로 사용된다. 이미지는 feature map이 VQ에 의해 양자화되고 재정렬된 후 이산 코드 시퀀스로 표현된다. 양자화 후에는 AR 모델이 코드 시퀀스를 순차적으로 예측하도록 학습된다. 이런 방법으로 AR 모델은 전체 픽셀을 예측하지 않고 높은 해상도의 이미지를 생성한다. AR은 이전 위치의 코드로 다음 코드를 예측하기 떄문에 코드 시퀀스가 짧으면 AR 모델의 계산 비용을 크게 줄일 수 있다. 따라서 코드 시퀀스의 길이를 줄이는 것이 이미지의 AR 모델링에 중요하다. 그러나 기존 연구들은 rate-disortion trade-off 측면에서 코드 시퀀스의 길이를 줄이는 데 한계가 있다. 즉, 코드 시퀀스가 너무 짧으면 정보의 압축 과정에서 손실이 많이 발생하고 손실을 줄이려면 코드 시퀀스가 길어진다. VQ-VAE의 경우, 재구성 이미지의 품질을 유지하면서 양자화된 feature map의 크기를 줄이려면 기하급수적으로 코드북의 크기가 즐가한다. 코드북의 크기가 크면 모델의 파라미터가 증가하고, codebook collapse 문제가 발생하여 학습이 불안정해진다.

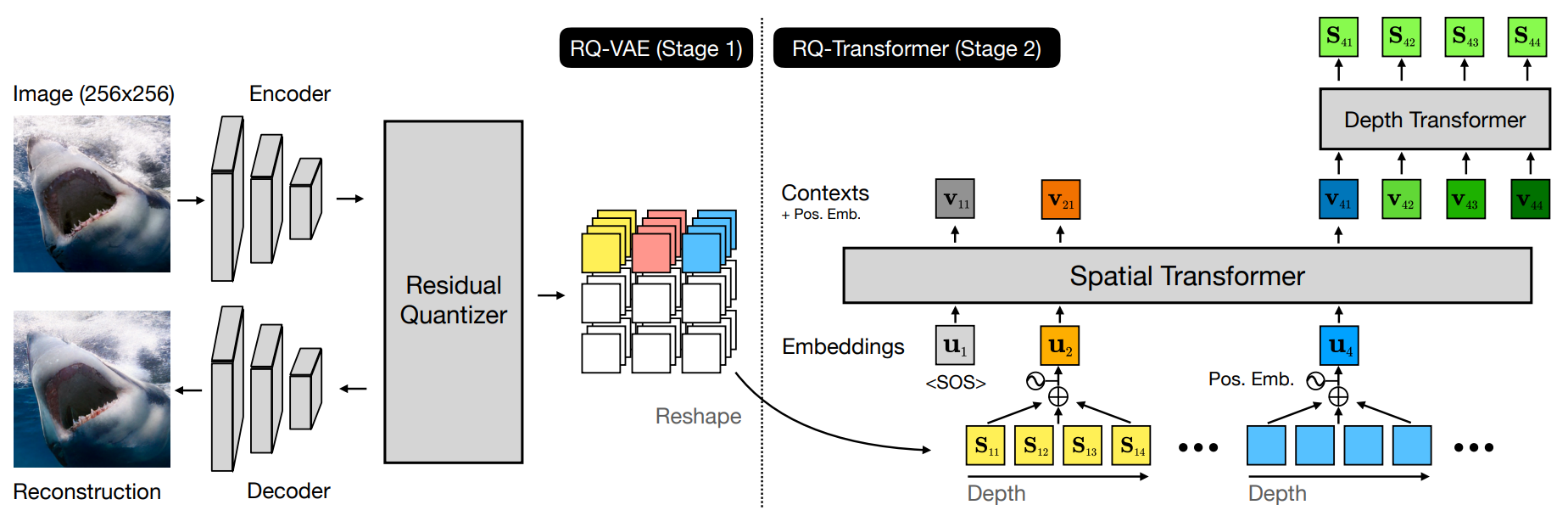
이 논문에서는 residual quantization (RQ)를 사용하여 feature map을 정확하게 근사하고 공간 해상도를 줄이는 Residual-Quantized VAE (RQ-VAE)를 제안한다. RQ는 코드북의 크기를 늘리는 대신 고정된 크기의 코드북을 사용하여 feature map을 재귀적으로 양자화한다. $D$ iteration 후 feature map은 $D$개의 이산 코드의 stacked map으로 표현된다. RQ는 코드북 크기의 $D$제곱만큼의 벡터로 구성할 수 있으므로 거대한 코드북 없이 이미지의 정보를 보존하면서 feature map을 정확하게 근사할 수 있다. 정확한 근사가 가능하기 때문에 RQ-VAE는 이전 연구보다 양자화된 feature map의 공간 해상도를 더 줄일 수 있다. 예를 들어, 256x256 이미지에 대한 모델은 8x8의 feature map을 사용한다.

추가로 저자들은 RQ-VAE에서 추출한 코드를 예측하기 위해 RQ-Transformer를 제안한다. RQ-VAE로 양자화된 feature map을 일련의 feature vector들로 변환하여 RQ-Transformer의 입력으로 준다. 그런 다음 RQ-Transformer가 다음 위치의 feature vetor들을 추정하기 위해 다음 $D$개의 코드를 예측한다. RQ-VAE가 feature map의 해상도를 줄여주기 때문에 RQ-Transformer는 계산 비용을 상당히 줄일 수 있으며 입력 이미지에서 멀리 떨어진 지점 사이의 관계를 쉽게 학습할 수 있다.

또한 저자들은 RQ-Transformer를 위한 2가지 학습 기법을 제안하였는데, 하나는 soft-labeling이고 다른 하나는 RQ-VAE에서 코드를 stochastic하게 sampling하는 것이다. 이는 학습 과정에서의 exposured bias를 해결하여 RQ-Transformer의 성능을 더욱 향상시킨다.

Methods

1. Stage 1: Residual-Quantized VAE

먼저 VQ와 VQ-VAE를 알아본 뒤 RQ-VAE가 어떻게 이미지를 이산 코드들의 stacked map으로 표현하는 지를 살펴보자.

1.1 Formulation of VQ and VQ-VAE

코드 $k$와 코드 임베딩 $\textbf{e}(k) \in \mathbb{R}^{n_z}$ 쌍으로 이루어진 코드북 $\mathcal{C}$를 유한 집합 \(\{(k, \textbf{e}(k))\}_{k \in [K]}\)로 정의한다. $K$는 코드북의 크기이며 $n_z$는 코드 임베딩의 차원이다. 주어진 벡터 $\textbf{z} \in \mathbb{R}^{n_z}$에 대하여, $\textbf{z}$의 VQ를 $\mathcal{Q}(z;\mathcal{C})$라 표기하며, 이는 $\textbf{z}$에 가장 가까운 코드 임베딩이다.

\[\begin{equation} \mathcal{Q}(\textbf{z};\mathcal{C}) = \underset{k \in [K]}{\arg \min} \| \textbf{z} - \textbf{e}(k) \|_2^2 \end{equation}\]

VQ-VAE는 이미지를 이산 코드맵으로 인코딩한 뒤, 인코딩된 이산 코드맵으로부터 원본 이미지를 재구성한다. $E$를 인코더, $G$를 디코더라 하자. 주어진 이미지 $\textbf{X} \in \mathbb{R}^{H_o \times W_o \times 3}$에 대하여 먼저 feature map $\textbf{Z} = E(\textbf{X}) \in \mathbb{R}^{H \times W \times n_z}$를 추출한다. 여기서 $f$가 downsampling factor이면 $(H, W) = (H_o / f, W_o / f)$이다. 다음과 같이 각 위치의 각 feature vector에 VQ를 적용하여 $Z$를 양자화하고 코드맵 $\textbf{M} \in [K]^{H \times W}$와 양자화된 feature map $\hat{\textbf{Z}} \in \mathbb{R}^{H \times W \times n_z}$을 리턴한다.

\[\begin{equation} \textbf{M}_{hw} = \mathcal{Q} (\textbf{Z}_{hw} ; \mathcal{C}), \quad \hat{\textbf{Z}}_{hw} = \textbf{e} (\textbf{M}_{hw}) \end{equation}\]

(\(\textbf{Z}_{hw} \in \mathbb{R}^{n_z}\)는 ($h$, $w$)에서의 feature vector, \(\textbf{M}_{hw}\)는 \(\textbf{Z}_{hw}\)에 대한 코드)

마지막으로 $\hat{\textbf{X}} = G(\hat{\textbf{Z}})$로 이미지를 재구성한다.

AR 모델의 계산 비용이 $HW$에 따라 증가하기 때문에 \(\hat{\textbf{Z}}\)의 공간 해상도 ($H$, $W$)를 줄이는 것이 중요하다. 하지만 ($H$, $W$)를 줄이면 이미지 압축 과정에서 손실이 발생하기 때문에 ($H$, $W$)를 줄이는 것과 $\textbf{X}$의 정보 보존 사이에 trade-off가 있다. 특히, 코드북의 크기가 $K$인 VQ-VAE는 $HW \log_2 K$ 비트를 코드로 이미지를 표현하는 데 사용한다. Rate-distortion 이론에 의하면 재구성 오차는 비트 수에 의존하기 때문에 재구성 오차를 유지하면서 공간 해상도를 ($H/2$, $W/2$)로 줄이려면 코드북의 크기를 $K^4$로 늘려야 한다. 코드북의 크기가 커지면 codebook collapse 문제로 인해 학습이 불안정해진다.

1.2 Residual Quantization

코드북의 코드를 증가시키는 대신 residual quantization (RQ)를 적용하면 문제를 해결할 수 있다. 주어진 양자화 깊이 $D$에 대하여, RQ는 $\textbf{z}$를 순서가 있는 $D$개의 코드로 표현한다.

\[\begin{equation} \mathcal{RQ} (\textbf{z} ; \mathcal{C}, D) = (k_1, \cdots k_D) \in [K]^D \end{equation}\]

($\mathcal{C}$는 크기가 $|\mathcal{C}| = K$인 코드북, $k_d$는 깊이 $d$에서의 $z$의 코드)

RQ는 0번째 residual $\textbf{r}_0 = \textbf{z}$부터 시작해서 재귀적으로 $k_d$를 계산한다. 이 때 $k_d$는 residual \(\textbf{r}_{d-1}\)의 코드이며 다음 residual은 $\textbf{r}_d$이다. 모든 $d = 1, \cdots, D$에 대하여

\[\begin{aligned} k_d &= \mathcal{Q} (\textbf{r}_{d-1}; \mathcal{C})\\ \textbf{r}_d &= \textbf{r}_{d-1} - \textbf{e} (k_d) \end{aligned}\]

이다. 또한, $\hat{\textbf{z}}^{(d)} = \sum_{i=1}^d \textbf{e} (k_i)$로 정의하고 $\hat{\textbf{z}} := \hat{\textbf{z}}^{(D)}$는 $\textbf{z}$의 양자화된 벡터이다.

RQ의 재귀적 양자화는 벡터 $\textbf{z}$를 coarse-to-fine 방식으로 근사한다. $\hat{\textbf{z}^{(1)}}$은 $\textbf{z}$에 가장 가까운 코드 임베딩 $\textbf{e}(k_1)$이다. 그런 다음 각 깊이에서 양자화 오차를 줄이기 위해 나머지 코드가 선택된다. 따라서 $d$까지의 부분합인 $\hat{\textbf{z}}^{(d)}$는 $d$가 증가함에 따라 더 fine한 근사값이다.

각 깊이 $d$에 대해 별도로 코드북을 구성할 수 있지만 모든 양자화 깊이에 대해 단일 공유 코드북 $\mathcal{C}$가 사용된다. 공유 코드북은 2가지 이점이 있다.

1. 별도의 코드북을 사용하려면 각 깊이에서 코드북 크기를 결정하기 위해 적합한 hyper-parameter를 찾아야 하지만 공유 코드북을 사용하면 전체 코드북 크기 $K$만 결정하면 된다.
2. 공유 코드북은 모든 양자화 깊이에 대해 모든 코드 임베딩을 사용할 수 있다. 따라서 코드는 모드 깊이에서 사용되어 유용성을 극대화할 수 있다.

RQ는 코드북 크기가 같을 때 VQ보다 더 정교하게 근사할 수 있다. VQ가 전체 벡터 공간 $\mathbb{R}^{n_z}$를 $K$ 클러스터로 분할하지만, 깊이가 $D$인 RQ는 벡터 공간을 $KD$ 클러스터로 분할한다. 즉, 길이가 $D$인 RQ는 $KD$개의 코드가 있는 VQ와 동일한 partition capacity를 갖는다. 따라서, VQ의 코드북을 기하급수적으로 증가시키는 것을 RQ의 $D$를 증가시키는 것으로 대체할 수 있다.

1.3 RQ-VAE

저자들은 이미지의 feature map을 정확하게 양자화하기 위해 RQ-VAE를 제안한다. RQ-VAE도 VQ-VAE의 인코더-디코더 구조로 구성되어 있지만 VQ 모듈은 RQ 모듈로 대체된다. 구체적으로, 깊이가 $D$인 RQ-VAE는 feature map $\textbf{Z}$를 코드 $\textbf{M} \in [K]^{H \times W \times D}$의 stacked map으로 표현된다. 그 다음 깊이 $d$에서 양자화된 feature map $\hat{\textbf{Z}}^{(d)} \in \mathbb{R}^{H \times W \times n_z}$를 추출한다.

\[\begin{aligned} \textbf{M}_{hw} &= \mathcal{RQ} (E(\textbf{X}); \mathcal{C}, D) \\ \hat{\textbf{Z}}_{hw}^{(d)} &= \sum_{d'=1}^d \textbf{e} (\textbf{M}_{hwd'}) \end{aligned}\]

깊이 $D$에서의 양자화된 feature map $\hat{\textbf{Z}}^{(D)}$를 $\hat{\textbf{Z}}$로 표기한다. 마지막으로 $\hat{\textbf{X}} = G(\hat{\textbf{Z}})$로 원본 이미지를 재구성한다.

RQ-VAE는 낮은 계산 비용으로 고해상도 이미지를 효과적으로 생성할 수 있다. 고정된 downsampling factor $f$에 대하여, RQ-VAE는 주어진 코드북 크기를 사용하여 feature map을 정확하게 근사할수 있으므로 RQ-VAE는 VQ-VAE보다 더 현실적으로 이미지를 재구성할 수 있다. 재구성된 이미지가 얼마나 정확하게 재구성되는지는 생성된 이미지의 최고 품질에 매우 중요하다. 또한, RQ-VAE에 의한 정확한 근사는 재구성 품질을 유지하면서 VQ-VAE보다 더 많이 $f$를 증가시킬 수 있고 더 많이 ($H$, $W$)을 감소시킬 수 있다.

1.4 Training of RQ-VAE

RQ-VAE의 인코더 $E$와 디코더 $D$를 학습하기 위해 loss \(\mathcal{L} = \mathcal{L}_{\textrm{recon}} + \beta \mathcal{L}_{\textrm{commit}} \; (\beta > 0)\)에 대한 gradient descent를 사용한다. Reconstruction loss \(\mathcal{L}_{\textrm{recon}}\)와 commitment loss \(\mathcal{L}_{\textrm{commit}}\)은 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_{\textrm{recon}} = \| \textbf{X} - \hat{\textbf{X}} \|_2^2 \\ \mathcal{L}_{\textrm{commit}} = \sum_{d=1}^D \bigg\| \textbf{Z} - \textrm{sg} \bigg[ \hat{\textbf{Z}}^{(d)} \bigg] \bigg\|_2^2 \end{equation}\]

(sg는 stop-gradient 연산자)

\(\mathcal{L}_{\textrm{recon}}\)은 모든 $d$에 대한 양자화 오차의 합이다. 이는 $d$가 증가함에 따라 $\hat{\textbf{Z}}^{(d)}$가 $\textbf{Z}$의 양자화 오차를 순차적으로 감소시키는 것을 목표로 한다. 따라서 RQ-VAE는 coarse-to-fine 방식으로 feature map을 근사하고 학습을 안정적으로 유지한다. 코드북 $\mathcal{C}$는 클러스터링된 feature의 exponential moving average에 의해 업데이트된다.

1.5 Adversarial Training of RQ-VAE

RQ-VAE는 adversarial training으로 재구성된 이미지의 perceptual quality를 개선한다. Patch-based adversarial loss와 perceptual loss가 이전 연구에서 사용한 것과 동일하게 사용되었다.

2. Stage 2: RQ-Transformer

2.1 AR Modeling for Codes with Depth $D$

RQ-VAE에서 코드맵 $\textbf{M} \in [K]^{H \times W \times D}$을 추출한 뒤 raster scan order로 $\textbf{M}$을 $\textbf{S} \in [K]^{T \times D}$ ($T = HW$)로 재정렬한다. 여기서 $\textbf{S}_t$는 $\textbf{S}$의 $t$번째 행으로 $D$개의 코드를 포함한다.

\[\begin{equation} \textbf{S}_t = (\textbf{S}_{t1}, \cdots, \textbf{S}_{tD} \in [K]^D) \quad \textrm{for} t \in [T] \end{equation}\]

$\textbf{S}$를 이미지의 이산 잠재 변수로 생각하면 AR 모델은 $p(\textbf{S})$를 학습한다.

\[\begin{equation} p(\textbf{S}) = \sum_{t=1}^T \sum_{d=1}^D p(\textbf{S}_{td} | \textbf{S}_{<t,d}, \textbf{S}_{t,<d}) \end{equation}\]

2.2 RQ-Transformer Architecture

Raster scan order로 $\textbf{S}$를 길이가 $TD$인 시퀀스로 전개한 뒤 일반적인 transformer에 입력으로 주어 학습하는 방법을 생각할 수 있다. 하지만 이 방법은 RQ-VAE에 의해 감소된 $T$를 활용하지 않고 계산 비용도 줄이지 않는다. 따라서 저자들은 RQ-VAE에서 깊이 $D$로 추출한 코드를 효율적으로 학습하기 위한 RQ-Transformer를 제안하였다. RQ-Transformer는 spatial transformer와 depth transformer로 이루어져 있다.

Spatial Transformer는 masked self-attention 블록의 스택이며 이전 위치의 정보를 요약하는 context vector를 추출한다. 입력으로 RQ-VAE의 학습된 코드북을 재사용하며, 입력 $\textbf{u}_t$를 다음과 같이 정의한다.

\[\begin{equation} \textbf{u}_t = \textrm{PE}_T (t) + \sum_{d=1}^D \textbf{e} (\textbf{S}_{t-1, d}) \quad \textrm{for} \; t > 1 \end{equation}\]

$\textrm{PE}_T (t)$는 raster scan order에서의 위치 $t$에 대한 positional embedding이다. 두번째 항은 양자화된 feature vector와 동일하다. 첫번째 위치($t = 1$)에 대한 입력을 위해 학습 가능한 embedding $\textbf{u}_1$을 정의한다. \((\textbf{u}_t)_{t=1}^T\)가 계산되면 다음과 같이 context vector $\textbf{h}_t$로 \(\textbf{S}_{< t}\)의 모든 정보를 인코딩한다.

\[\begin{equation} \textbf{h}_t = \textrm{SpatialTransformer} (\textbf{u}_1, \cdots, \textbf{u}_t) \end{equation}\]

Depth Transformer는 주어진 context vector $\textbf{h}_t$에 대하여 위치 $t$에서 autoregressive하게 $D$개의 코드 \((\textbf{S}_{t1}, \cdots, \textbf{S}_{tD})\)를 예측한다. 위치 $t$와 깊이 $d$에 대하여 depth transformer의 입력 \(\textbf{v}_{td}\)를 깊이 $d-1$까지의 코드 임베딩의 합으로 정의한다.

\[\begin{equation} \textbf{v}_{td} = \textrm{PE}_D (d) + \sum_{d'=1}^{d-1} \textbf{e} (\textbf{S}_{t, d'}) \quad \textrm{for} \; d > 1 \end{equation}\]

$\textrm{PE}_D (d)$는 깊이 $d$에 대한 positional embedding이며 모든 위치 $t$에 대하여 같은 값을 갖는다. 위치 정보는 이미 $\textbf{u}_t$에서 인코딩되었기 때문에 \(\textbf{v}_{td}\)에는 $\textrm{PE}_T (t)$를 사용하지 않는다. $d=1$에 대해서는 \(v_{t1} = \textrm{PE}_D (1) + h_t\)를 사용한다. 두번째 항은 깊이 $d-1$에서 양자화된 feature vector \(\hat{\textbf{Z}}_{hw}^{(d-1)}\)에 해당한다. 따라서 depth transformer는 $d-1$까지의 추정을 기반으로 더 fine한 $\hat{\textbf{Z}}_t$ 추정을 위한 다음 코드를 예측한다. 마지막으로, depth transformer는 다음과 같이 조건부 확률 분포 \(\textbf{p}_{td} (k) = p (\textbf{S}_{td} = k \vert \textbf{S}_{<t,d}, \textbf{S}_{t,< d})\)를 예측한다.

\[\begin{equation} \textbf{p}_{td} = \textrm{DepthTransformer} (\textbf{v}_{t1}, \cdots, \textbf{v}_{td}) \end{equation}\]

RQ-Transformer는 negative log-likelihood (NLL) loss $\mathcal{L}_{AR}$를 최소화하도록 학습된다.

\[\begin{equation} \mathcal{L}_{AR} = \mathbb{E}_{\textbf{S}} \mathbb{E}_{t,d} [-\log p(\textbf{S}_{td} = k \vert \textbf{S}_{<t,d}, \textbf{S}_{t,< d})] \end{equation}\]

Computational Complexity

RQ-Transformer의 계산 복잡도를 계산해보자. 길이가 $TD$인 시퀀스를 $N$ layer의 transformer로 계산할 때의 계산 복잡도는 $O(NT^2 D^2)$이다. 반면 $N_{\textrm{spatial}}$ layer의 spatial transformer와 $N_{\textrm{depth}}$ layer의 depth transformer로 이루어진 총 $N$ layer인 RQ-Transformer의 경우, 계산 복잡도가 각각 $O(N_{\textrm{spatial}} T^2)$과 $O(N_{\textrm{depth}} T D^2)$이다. 즉, 총 계산 복잡도는 $O(N_{\textrm{spatial}} T^2 + N_{\textrm{depth}} T D^2)$이고, 이는 $O(NT^2 D^2)$보다 굉장히 작다.

2.3 Soft Labeling and Stochastic Sampling

Exposure bias는 학습과 inference에서의 예측의 불일치로 인한 오차 누적으로 인해 AR 모델의 성능을 저하시키는 것으로 알려져 있다. RQ-Transformer의 경우, $d$가 증가함에 따라 feature vector를 더 fine하게 추정하기가 어려워지기 때문에 깊이 $D$와 함께 예측 오차도 누적될 수 있다. 따라서, 저자들은 soft labeling과 stochastic sampling으로 exposure bias를 해결하고자 하였다.

학습과 inference의 예측의 불일치를 줄이는 대표적인 방법은 scheduled sampling이다. 하지만 각 학습 단계마다 여러 inference가 필요하고 학습에 대한 계산 비용이 증가하므로 대규모 AR 모델에는 적합하지 않다. 그 대신 RQ-VAE에서 코드 임베딩의 기하학적 관계를 활용한다. 벡터 $\textbf{z} \in \mathbb{R}^{n_z}$를 조건부로 하는 $[K]$에 대한 카테고리 분포를 $\mathcal{Q}_\tau (k \vert \textbf{z})$로 정의한다. 여기서 $\tau > 0$은 temperature이다.

\[\begin{equation} \mathcal{Q}_\tau (k \vert \textbf{z}) \propto e^{-\| \textbf{z} - \textbf{e}(k) \|_2^2 / \tau} \quad \textrm{for} \; k \in [K] \end{equation}\]

$\tau$가 0에 가까워지면 $\mathcal{Q}_\tau$는 뾰족해지며 one-hot 분포 $\mathcal{Q}_0 (k \vert \textbf{z}) = \textbf{1} [k = \mathcal{Q} (\textbf{z}; C)]$ 로 수렴한다.

Soft Labeling of Target Codes

코드 임베딩들 사이의 거리를 기반으로 하여, soft labeling은 RQ-VAE의 코드들 사이의 기하학적 관계에 대한 supervision을 통해 RQ-Transformer의 학습을 개선한다. 위치 $t$와 깊이 $d$에 대하여 $\textbf{Z}_t$를 이미지의 feature vector라 하고 \(\textbf{r}_{t,d-1}\)을 깊이 $d-1$에서의 residual vector라 하자. 그러면 NLL loss는 \(\mathcal{Q}_0 (\cdot \vert \textbf{r}_{t,d-1})\)를 \(\textbf{S}_{td}\)의 supervision으로 사용한다. One-hot 분포 \(\mathcal{Q}_0 (\cdot \vert \textbf{r}_{t,d-1})\)를 사용하는 대신 부드러운 분포 \(\mathcal{Q}_\tau (\cdot \vert \textbf{r}_{t,d-1})\)를 사용한다.

Stochastic Sampling for Codes of RQ-VAE

저자들은 학습과 inference의 불일치를 줄이기 위해 RQ-VAE에서 코드 맵의 stochastic sampling을 제안한다. RQ에서 코드를 deterministic하게 선택하는 대신 \(\mathcal{Q}_\tau (\cdot \vert \textbf{r}_{t,d-1})\)에서 샘플링하여 코드 \(\textbf{S}_{td}\)를 선택한다. Stochastic sampling은 이미지의 주어진 feature map에 대하여 코드 $\textbf{S}$의 다양한 구성을 제공한다.

Experiments

• RQ-VAE 구조는 공정한 비교를 위해 VQ-GAN과 동일한 모델 구조를 사용. 추가로 8x8까지 feature map의 크기를 줄이기 위해 인코더와 디코더에 512채널의 residual block 1개씩 추가.
• RQ-Transformer는 Attention is all you need의 self-attention block을 쌓아서 구현
• RQ-VAE의 training details:
  • ImageNet: 10 epochs, batch size 128, Adam optimizer ($\beta_1 = 0.5$, $\beta_2 = 0.9$), lr = 4e-5 (0.5 epoch warm-up)
  • lr decay 없음, weight decay 없음, dropout 없음
  • LSUN: ImageNet에서 pre-train한 모델을 finetune. 1 epoch, lr = 4e-6
  • FFHQ: 150 epochs, lr = 4e-5 (5 epoch warm-up)
  • CC-3M: finetuning 없이 ImageNet에서 pre-train한 모델 사용
• RQ-Transformer의 training details:
  • Adam-W optimizer ($\beta_1 = 0.9$, $\beta_2 = 0.95$), lr = 5e-4 (cosine lr schedule), weight decay 1e-4,
  • batch size: FFHQ는 16, 나머지는 2048
  • dropout = 0.1 (3.8B 모델만 0.3)
  • 1.4B 모델은 NVIDIA A100 GPU 8개로 다른 모델은 4개로 학습
  • LSUN-cat, LSUN-bedroom은 9일, ImageNet, CC-3M은 4.5일, LSUN-church, FFHQ는 1일 학습
  • FFHQ는 39 epoch에서 early stopping
• 각 모델에 대한 하이퍼 파라미터는 아래와 같음

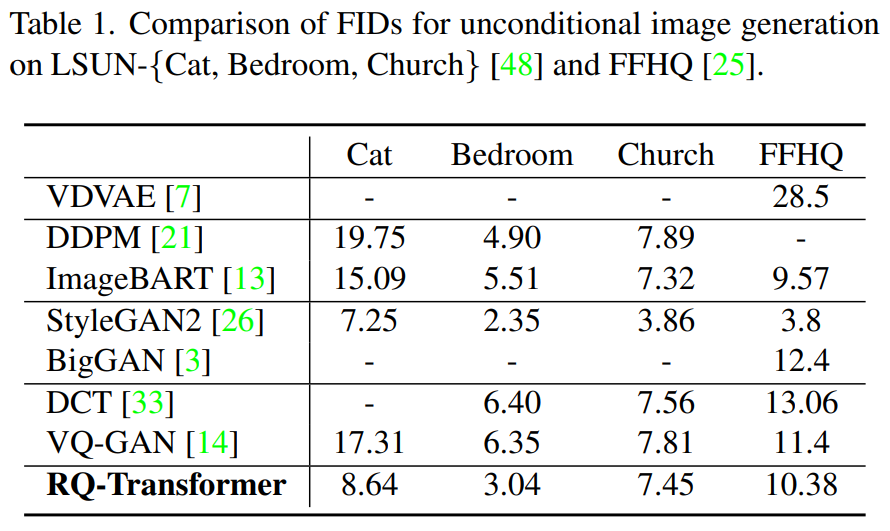
1. Unconditional Image Generation

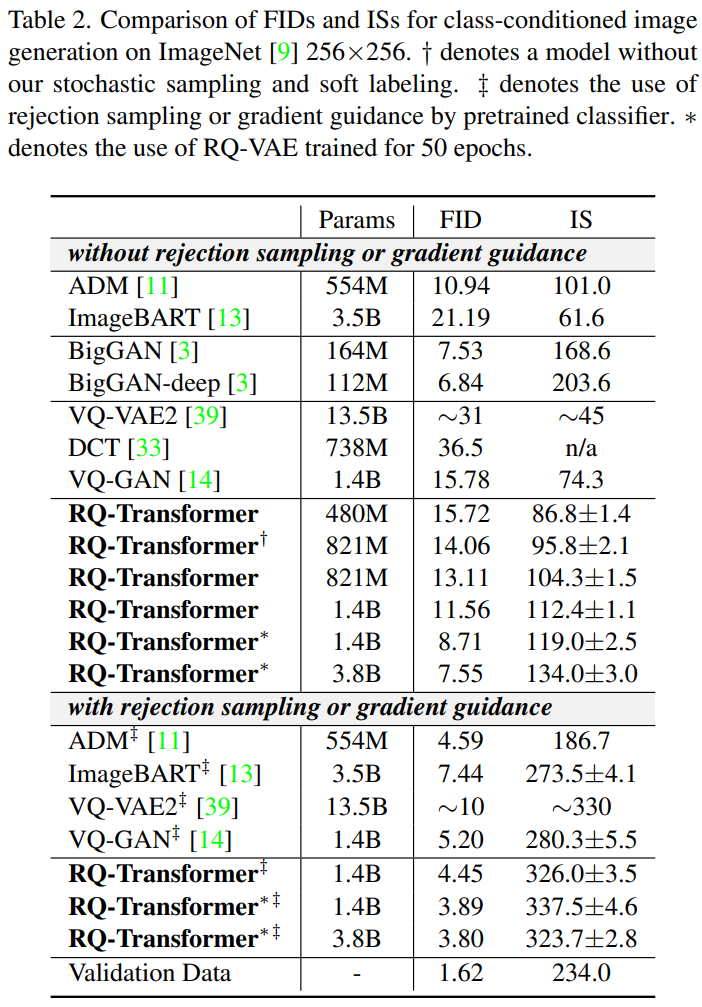
2. Conditional Image Generation

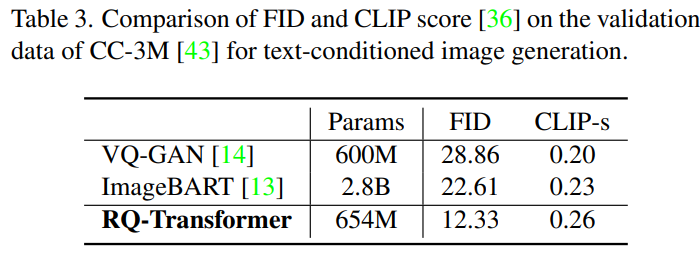
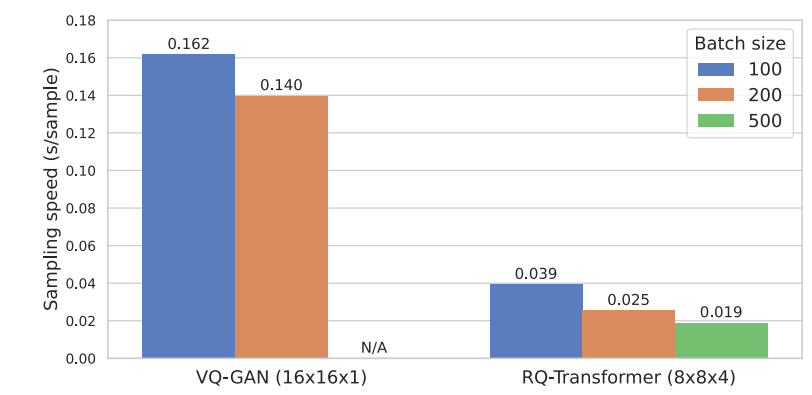
3. Computational Efficiency of RQ-Transformer

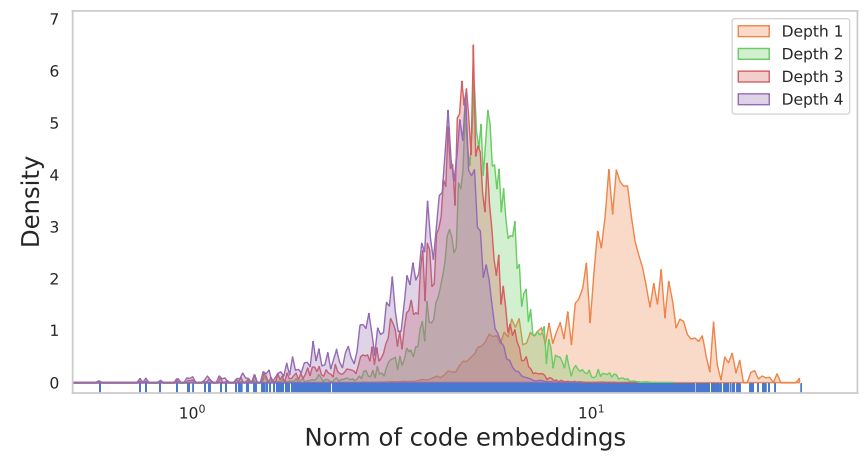
4. Ablation Study on RQ-VAE