Blogs

ICLR 2022. [Paper] [Github]
Dmitry Baranchuk, Ivan Rubachev, Andrey Voynov, Valentin Khrulkov, Artem Babenko
Yandex Research
6 Dec 2021

Introduction

DDPM has recently outperformed other approaches to modeling the distribution of natural images in both realism and variety of individual samples. This advantage of DDPM is successfully exploited in applications such as colorization, inpainting, super-resolution, and semantic editing where DDPM often achieves more impressive results compared to GANs.

However, until now, DDPM has not been utilized as an effective image representation source for discriminative computer vision problems. Although previous studies have shown that representations can be extracted for general vision tasks using various generative models, such as GANs or autoregressive models, it is unclear whether DDPM can serve as a representation learner. In this paper, we provide a positive answer to this question in the context of semantic segmentation.

In particular, we investigate the intermediate activation of the U-Net network close to the Markov step of the reverse diffusion process in DDPM. Intuitively, this network learns to denoise the input, and it is not clear why intermediate activations should capture the semantic information required for high-level vision problems. Nonetheless, the authors show that activations at specific diffusion steps capture such information and can potentially be used as image representations for downstream tasks. Given these observations, the authors propose a simple semantic segmentation method that exploits these representations and works successfully even when only a few labeled images are provided.

Representations from Diffusion Models

Background

Forward diffusion process:

\[\begin{equation} q(x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \\ q(x_t \vert x_0) := \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I), \\ x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I), \\ \textrm{where} \quad \alpha_t := 1 - \beta_t, \; \bar{\alpha}_t := \prod_{s=1}^t \alpha_s \end{equation}\]

Reverse process:

\[\begin{equation} p_\theta (x_{t-1}, x_t) := \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t) \Sigma_\theta (x_t, t)) \end{equation}\]

Extracting representations

Given a real image $x_0 \in \mathbb{R}^{H \times W \times 3}$, the noise prediction network $\epsilon_\theta (x_t, t)$ computes sets of activation tensors. can First, $x_0$ is corrupted by adding Gaussian noise according to the forward process equation. Noisy $x_t$ is used as input to $\epsilon_\theta (x_t, t)$ parameterized by the UNet model. Then, the intermediate activations of UNet are upsampled to $H \times W$ using bilinear interpolation. This allows us to process it as a pixel-level representation of $x_0$.

1. Representation Analysis

The authors analyzed the representations generated by $\epsilon_\theta (x_t, t)$ for different $t$, and state-of-the-art DDPM checks learned on the LSUN-Horse and FFHQ-256 datasets. use points

For this experiment, we take several images from the LSUN-Horse and FFHQ datasets and manually assign each pixel to one of the 21 and 34 semantic classes respectively. The authors’ goal is to understand whether the pixel-level representation generated by DDPM effectively captures semantic information. To do this, we train the MLP to predict pixel semantic labels from features generated by one of the 18 UNet decoder blocks at a specific diffusion step $t$. Since encoder activations are also counted through skip connection, only decoder activations are considered. The MLP is trained with 20 images and evaluated with 20 hold-out images. Prediction performance is measured in average IoU.

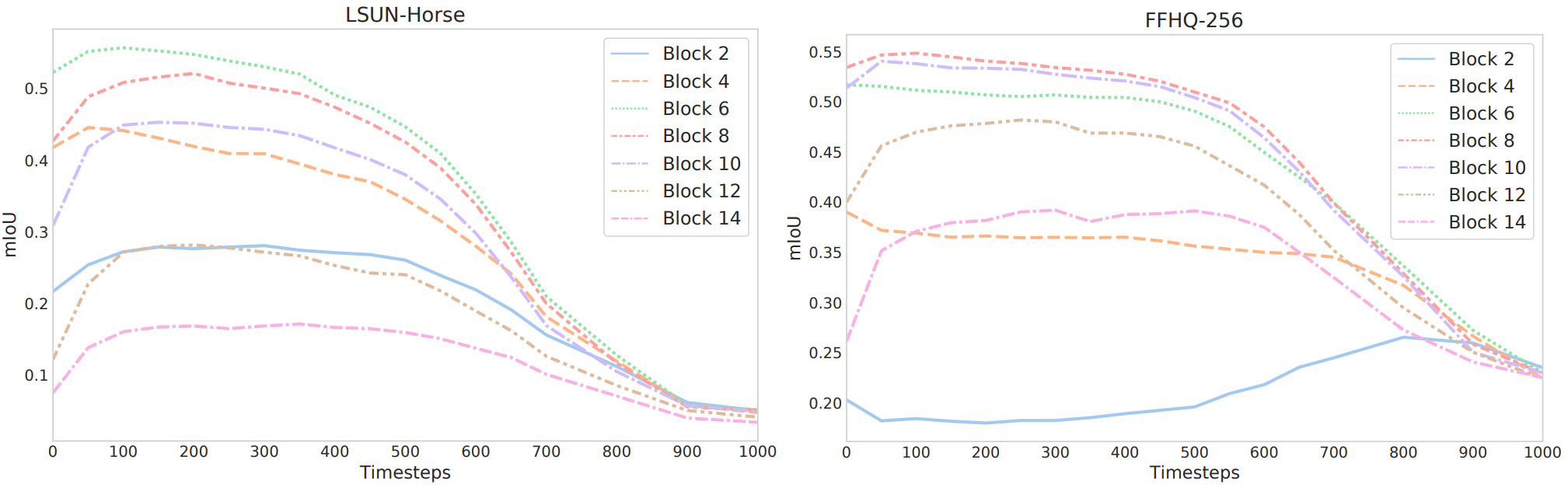
The evolution of prediction performance according to different blocks and $t$ is shown in the graph above. The blocks are numbered from deep to shallow. The graph above shows that the identifiability of a feature generated by $\epsilon_\theta (x_t, t)$ depends on the block and $t$. In particular, features corresponding to later steps in the reverse diffusion process usually capture semantic information more effectively. In contrast, those corresponding to the initial steps are generally uninformative. In several blocks, the features generated by the layers in the middle of the UNet decoder appear to be the most informative for all diffusion steps.

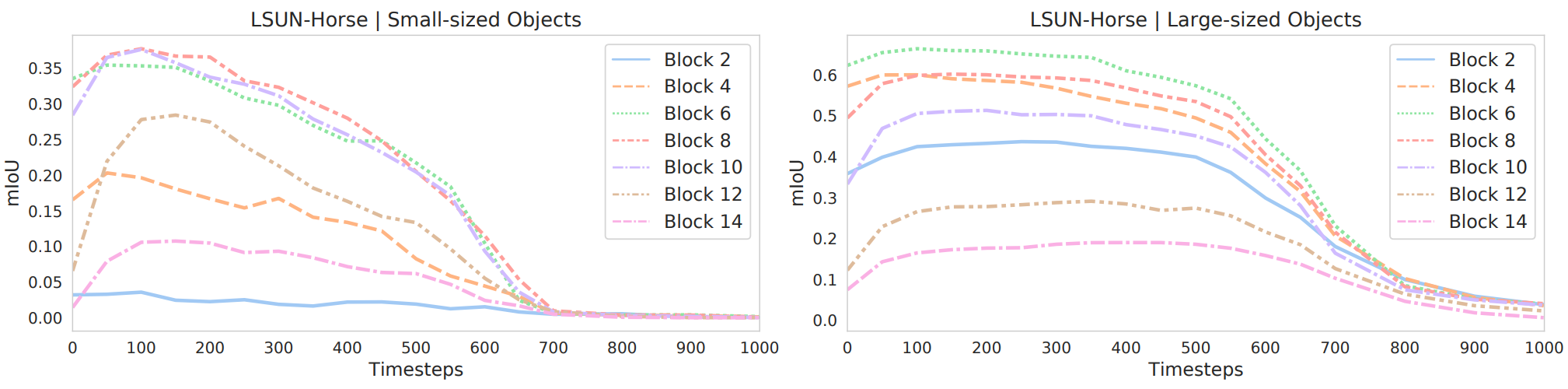
In addition, based on the average area of the annotated dataset, small semantic class and large semantic class are considered separately. We then independently evaluate the average IoU for these classes in different UNet blocks and diffusion steps. The results for LSUN-Horse are shown in the graph above. As expected, the prediction performance for large objects starts to increase earlier in the reverse process. Shallower blocks provide more information for smaller objects, while deeper blocks provide more information for larger objects. In both cases, the most discriminative feature still corresponds to the middle block.

This means that for a specific UNet block and diffusion step, similar DDPM-based representations correspond to pixels of the same semantic. The figure above shows k-means clusters ($k=5$) formed by features extracted by FFHQ checkpoints of blocks {6, 8, 10, 12} in diffusion step {50, 200, 400, 600, 800}. shows It can be seen that the cluster can cover consistent semantic objects and object parts. In block $B=6$, the feature corresponds to an approximate semantic mask. On the other hand, the feature of $B=12$ can distinguish fine facial parts, but shows less semantic meaning for rough pieces.

In the various diffusion steps, the most meaningful features correspond to the later features. This behavior is due to the fact that it is almost impossible to predict the segmentation mask at the initial step of the reverse process because the global structure of the DDPM samples has not yet emerged. This intuition is qualitatively confirmed by the mask in the figure above. In the case of $t=800$, the mask does not properly reflect the contents of the actual image, whereas for smaller values of $t$, the mask and image are semantically consistent.

2. DDPM-Based Representations for Few-Shot Semantic Segmentation

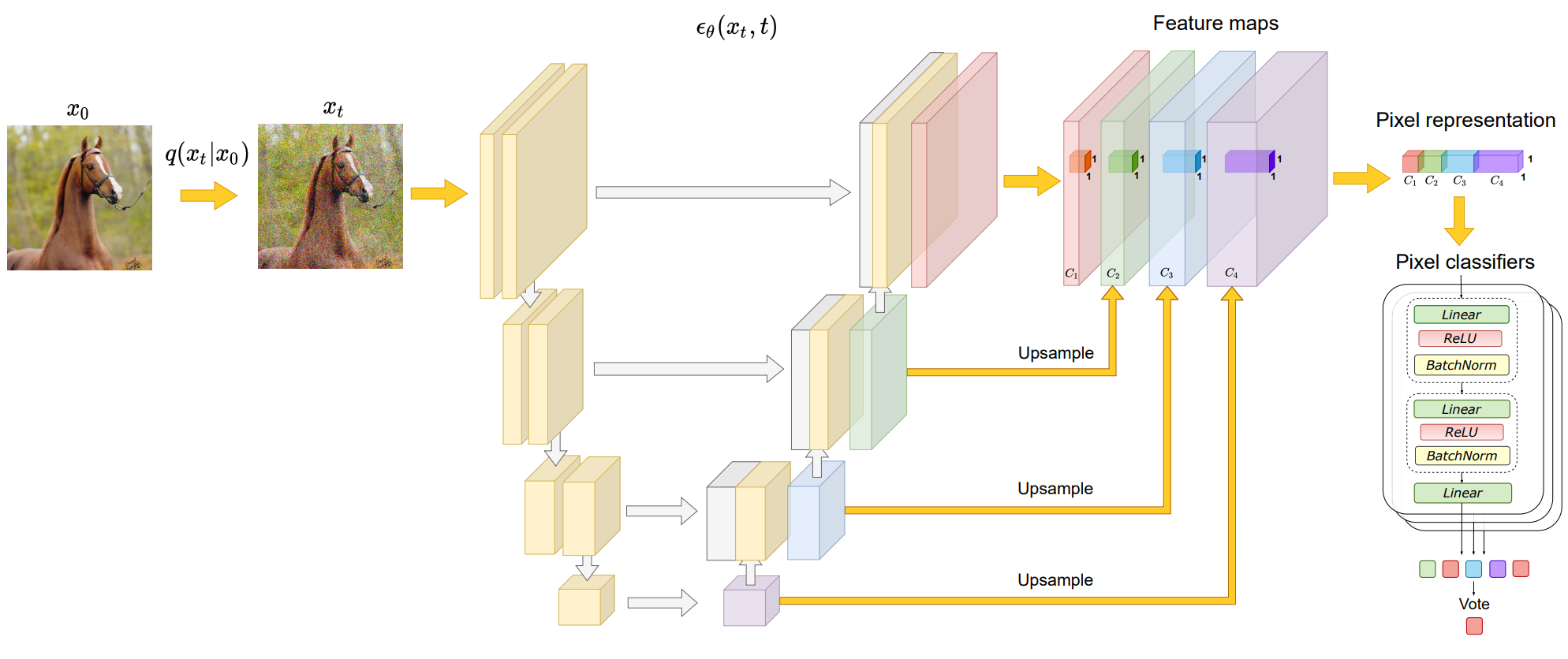
The potential effect of intermediate DDPM activation observed above implies its use as an image representation for dense prediction tasks. The figure above outlines an overall approach to image segmentation that exploits the distinctiveness of these representations.

A large number of unlabeled images \(\{X_1, \cdots, X_N\} \subset \mathbb{R}^{H \times and \times 3}\) are available in a particular domain, $n ground-truth $K$-class semantic masks \(\ only for $ training images\){X_1, \cdots, X_n} \subset \mathbb{R}^{H \times W \times 3}\({Y_1, \cdots, Y_n\} \subset \mathbb{R}^{H \times W \times \{1, \cdots, K\}}\) is provided.

As a first step, the diffusion model is trained in an unsupervised way from all \(\{X_1, \cdots, X_N\}\). This diffusion model is then used to extract pixel-level representations of labeled images using subsets of UNet blocks and t. In this paper, the middle block \(B = \{5, 6, 7, 8, 12\}\) of the UNet decoder and the later step \(t = \{50, 150, 250\}\) of the reverse diffusion process use the expression

Feature extraction at a specific timestep is stochastic, but we fix and remove noise for all timesteps. The representations extracted from all $B$ and $t$ are upsampled and concated to the image size to form a feature vector for all pixels in the training image. The total dimension of the pixel level representation is 8448.

Then, we train an ensemble of independent MLPs on these feature vectors, aiming to predict a semantic label for each pixel that can be used for image learning by following DatasetGAN. The authors adopt DatasetGAN’s ensemble construction and training setup and utilize it in all methods of experimentation.

To segment the test image, we extract the DDPM-based pixel-wise representation and use it to predict the pixel label by the ensemble. The final prediction is determined by majority vote of the ensemble.

Experiments

• dataset
  • LSUN (bedroom, cat, horse) $\rightarrow$ Bedroom-28, Cat-15, Horse-21
  • FFHQ-256 $\rightarrow$ FFHQ-34
  • ADE-Bedroom-30 (subset of ADE20K)
  • CelebA-19 (subset of CelebAMask-HQ)

The number of annotated images for each dataset is shown in the table below.

1. Main results

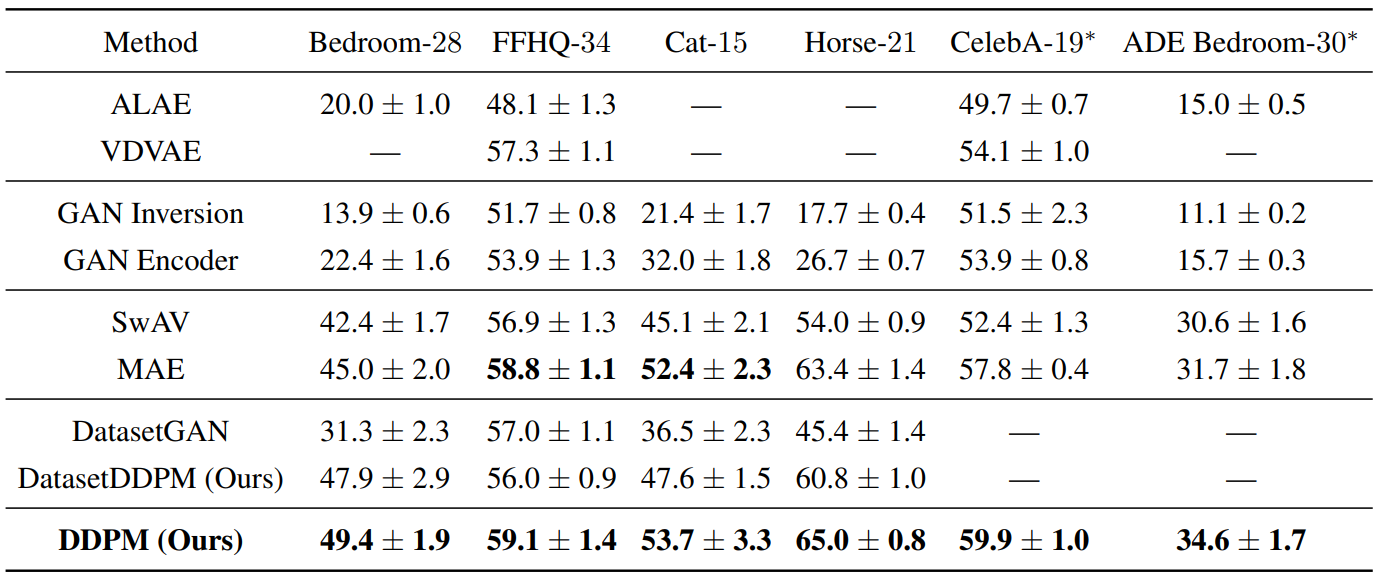
The following table compares segmentation methods by average IoU.

The following is an example of a segmentation mask predicted by our method on a test image with a ground-truth annotated mask.

2. The effect of training on real data

The following table compares the performance of DDPM-based segmentation when trained with real and synthesized images.

Learning on real images is highly informative in domains where the fidelity of generative models is still relatively low (e.g. LSUN-Cat), indicating that annotated real images are a more reliable source of supervision. Also, if the DDPM method is trained with synthetic images, its performance becomes equivalent to DatasetDDPM. On the other hand, when learning samples generated by GAN, DDPM shows much better performance than DatasetGAN. The authors attribute this to the fact that DDPM provides a more semantically valuable pixel-by-pixel representation compared to GANs.

3. Sample-efficiency

The following table evaluates the method in this paper with different numbers of labeled training data.

4. The effect of stochastic feature extraction

The following is a table showing the performance of the DDPM-based method for various feature extraction variants.

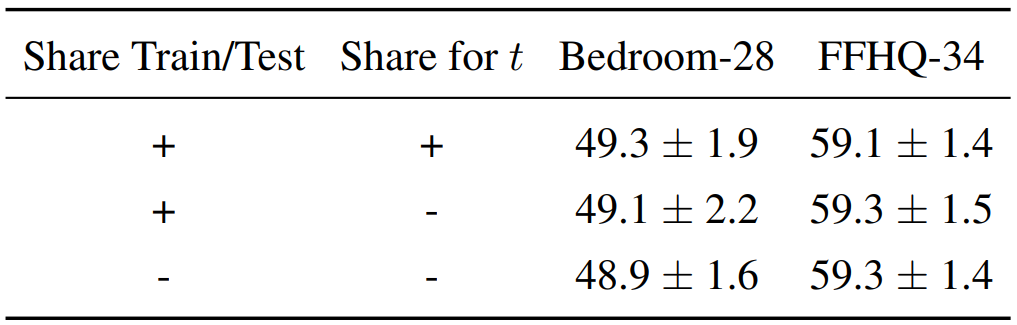
The difference in performance is minor. This behavior occurs for the following reasons.

1. The method in this paper uses the latter $t$ of the reverse diffusion process with low noise level.
2. Since the layer of the UNet model is used, noise may not greatly affect the activation of the layer.

5. Robustness to input corruptions

The following table shows the mIoU degradation for various image impairment levels in the Bedroom-28 and Horse-21 datasets.

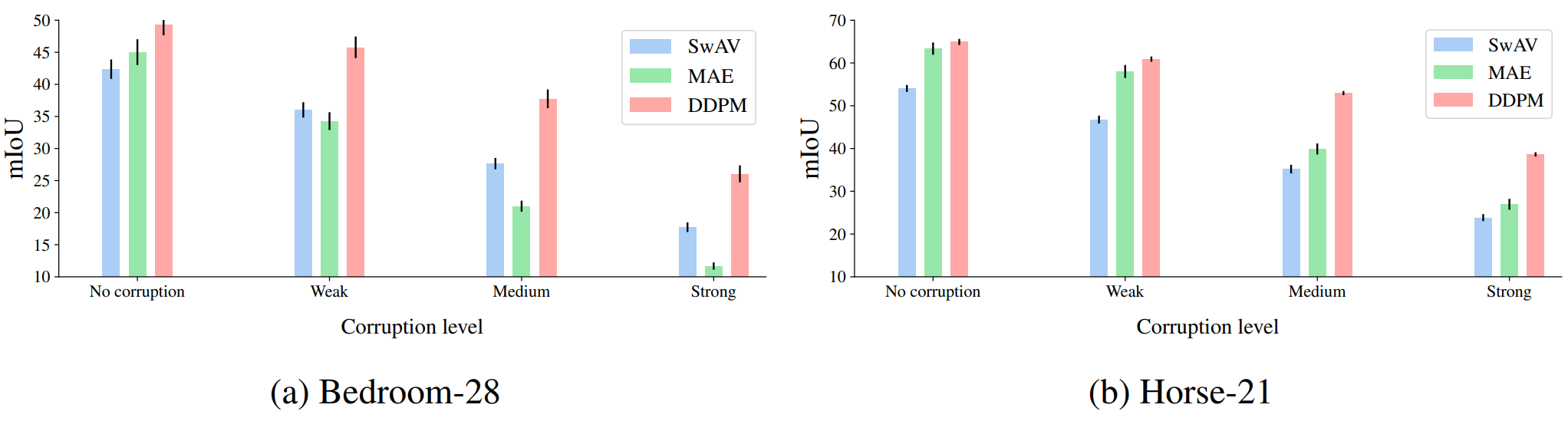
It can be observed that the proposed DDPM-based method maintains higher robustness and advantages than the SwAV and MAE models even under severe image distortion.