ICML 2022. [Paper]
Dongjun Kim, Seungjae Shin, Kyungwoo Song, Wanmo Kang, Il-Chul Moon
KAIST | University of Seoul | Summary.AI
10 Jun 2021
Introduction
이전에는 DDPM과 ADM과 같이 FID에 중점을 둔 모델이 variance weighting으로 score 네트워크를 학습했다. 반면 ScoreFlow와 VDM과 같이 NLL(Negative Log-Likelihood)에 중점을 둔 모델은 likelihood weighting으로 score 네트워크를 학습한다. 그러나 이러한 모델들은 NLL과 FID 사이에 trade-off가 있습니다. FID에 중점을 둔 모델은 NLL이 제대로 나오지 않으며 그 반대도 마찬가지이다. Trade-off를 광범위하게 조사하는 대신 FID에 유리한 설정과 NLL에 유리한 설정에서 score 네트워크를 별도로 학습하여 작업을 제한한다. 본 논문에서는 NLL에 유리한 설정을 기본 학습 구성으로 사용하여 trade-off를 크게 해결하는 Soft Truncation을 소개한다. Soft Truncation은 NLL에 유리한 모델과 동등한 수준의 NLL을 유지하면서 FID에 유리한 diffusion model에 대해 유사한 FID를 보인다.
이를 위해 truncation hyperparameter는 NLL과 FID의 전체 scale을 결정하는 중요한 hyperparameter이다. 이 hyperparameter $\epsilon$는 score 함수를 추정하기 위한 최소 diffusion time이며, $\epsilon$ 아래의 score 함수는 추정하지 않는다. $epsilon$이 충분히 작은 모델은 FID를 희생하지만 NLL을 선호하고, 상대적으로 큰 모델은 FID를 더 선호되지만 NLL이 좋지 않다. 따라서 고정된 정적 truncation hyperparameter ($\epsilon$)을 확률 변수 $\tau$로 부드럽게 만들며, 각 optimization step에서 최소 diffusion time을 랜덤하게 선택한다. 모든 mini-batch 업데이트에서 새로운 최소 diffusion time $tau$ 를 랜덤하게 샘플링하고 batch 최적화는 $\tau$ 아래를 무시하여 $[\epsilon, T]$가 아닌 $[\tau, T]$에서만 score 함수를 추정한다. $\tau$가 mini-batch 업데이트에 따라 달라지기 때문에 score 네트워크는 diffusion time의 전체 범위에 대한 score 함수를 성공적으로 추정하여 개선된 FID를 제공한다.
Soft Truncation에는 두 가지 흥미로운 속성이 있다. 첫째, Soft Truncation은 알고리즘 디자인에서 가중치 함수와 관련이 없지만 놀랍게도 기대값 측면에서 일반적인 가중치를 갖는 diffusion model과 동일하다. $\tau$의 확률 변수는 가중치 함수를 결정하며, 이는 FID를 선호하는 학습만큼 FID에서도 성공하는 부분적인 이유를 제공한다. 둘째, $\tau$가 mini-batch 최적화에서 샘플링되면 Soft Truncation은 $\tau$에 의해 교란된 log-likelihood를 최적화한다. 따라서 Soft Truncation은 diffusion model에서만 특별히 정의되는 MLE의 일반화된 개념인 MPLE(Maximum Perturbed Likelihood Estimation)로 구성될 수 있다.
Preliminary
본 논문에서는 연속시간 diffusion model을 다룬다. Diffusion은 다음과 같은 SDE로 표현된다.
\[\begin{equation} dx_t = f(x_t, t) dt + g(t) d w_t \end{equation}\]$w_t$는 standard Wiener process이다. 이 SDE에 대응되는 reverse SDE는 다음과 같다.
\[\begin{equation} dx_t = [f(x_t, t) - g^2 (t) \nabla \log p_t (x_t)] d \bar{t} + g(t) d \bar{w}_t \end{equation}\]Diffusion model의 목적은 \(\{x_t\}\)를 parameterize된 \(\{x_t^\theta\}\)로 학습하는 것이다. Parameterize된 생성 프로세스는 다음과 같다.
\[\begin{equation} dx_t^\theta = [f(x_t^\theta, t) - g^2 (t) s_\theta (x_t^\theta, t)] d \bar{t} + g(t) d \bar{w}_t \end{equation}\]Diffusion model은 다음과 같은 score loss를 최소화하여 생성 프로세스를 학습한다.
\[\begin{equation} \mathcal{L} (\theta; \lambda) = \frac{1}{2} \int_0^T \mathbb{E}_{x_t} [\| s_\theta (x_t, t) - \nabla \log p_t (x_t) \|_2^2 ] dt \end{equation}\]$\lambda (t)$는 각 diffusion time의 기여도를 나타내는 가중치 함수이다. $\nabla \log p_t (x_t)$가 일반적으로 tractable하지 않기 때문에 이 score loss는 사용할 수 없다. 다행히도 $\mathcal{L} (\theta; \lambda)$는 denoising NCSN loss와 동등하다.
\[\begin{equation} \mathcal{L}_{NCSN} (\theta; \lambda) = \frac{1}{2} \int_0^T \lambda (t) \mathbb{E}_{x_0, x_t} [\| s_\theta (x_t, t) - \nabla \log p_{0t} (x_t \vert x_0) \|_2^2] dt \end{equation}\]Variance Exploding SDE (VESDE)와 Variance Preserving SDE (VPSDE)는 수치적 전이 확률을 도달하는 것으로 알려져 있다. VESDE는
\[\begin{equation} f(x_t, t) = 0, \quad g(t) = \sigma_{min} \bigg( \frac{\sigma_{max}}{\sigma_{min}} \bigg)^t \sqrt{2 \log \frac{\sigma_{max}}{\sigma_{min}}} \end{equation}\]로 가정하며, VESDE의 전이 확률은 다음과 같은 가우시안 분포이다.
\[\begin{equation} p_{0t} (x_t \vert x_0) = \mathcal{N} (x_t; \mu_{VE} (t) x_0, \sigma_{VE}^2 (t) I) \\ \mu_{VE} (t) = 1, \quad \sigma_{VE}^2 = \sigma_{min}^2 \bigg[ \bigg( \frac{\sigma_{max}}{\sigma_{min}} \bigg)^{2t} -1 \bigg] \end{equation}\]VPSDE는
\[\begin{equation} f(x_t, t) = -\frac{1}{2} \beta(t) x_t, \quad g(t) = \sqrt{\beta(t)} \\ \beta(t) = \beta_{min} + t (\beta_{max} - \beta_{min}) \end{equation}\]로 가정하며, VESDE의 전이 확률은 다음과 같은 가우시안 분포이다.
\[\begin{equation} p_{0t} (x_t \vert x_0) = \mathcal{N} (x_t; \mu_{VP} (t) x_0, \sigma_{VP}^2 (t) I) \\ \mu_{VP} (t) = e^{- \frac{1}{2} \int_0^t \beta (s) ds}, \quad \sigma_{VP}^2 = 1 - e^{- \int_0^t \beta (s) ds} \end{equation}\]VESDE와 VPSDE는 다음과 같은 linear diffusion의 군으로 범주화할 수 있다.
\[\begin{equation} dx_t = -\frac{1}{2} \beta (t) x_t dt + g(t) dw_t \end{equation}\]이때 전이 확률은 가우시안 분포 $p_{0t} (x_t \vert x_0) = \mathcal{N}(x_t; \mu (t) x_0, \sigma^(t) I)$이며, $\mu (t)$와 $\sigma (t)$는 $\beta (t)$와 $g(t)$에 의존한다.
Soft Truncation은 어떠한 SDE에도 적용 가능하지만, 위 식의 linear SDE의 군으로 제한한다. 이 가우시안 전이 확률을 사용하면 denoising NCSN loss는 다음과 같다.
\[\begin{equation} \frac{1}{2} \int_0^T \frac{\lambda(t)}{\sigma^2 (t)} \mathbb{E}_{x_0, \epsilon} [\|\epsilon_\theta (\mu(t) x_0 + \sigma(t) \epsilon, t) - \epsilon \|_2^2 ] dt \end{equation}\]만일
\[\begin{equation} \epsilon_\theta (\mu(t) x_0 + \sigma(t)\epsilon, t) = -\sigma(t) s_\theta (\mu(t) x_0 + \sigma(t) \epsilon, t), \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]이면, $\epsilon_\theta$는 $\epsilon$를 예측하는 신경망이며, 이는 DDPM loss이다. 따라서 NCSN과 DDPM는 서로 교환 가능하며, 본 논문에서는 NCSN loss를 loss의 기본 형태로 한다.
가중치 함수가 $\lambda(t) = g^2 (t)$이면, NCSN loss는 다음과 같이 likelihood 학습과 연결된다.
\[\begin{equation} \mathbb{E}_{x_0} [-\log p_0^\theta (x_0)] \le \mathcal{L}_{NCSN} (\theta; g^2) \end{equation}\]이를 likelihood weighting이라 한다.
Training and Evaluation of Diffusion Models in Practice
1. The Need of Truncation
Linear SDE의 군에서 전이 확률의 로그 기울기는
\[\begin{equation} \nabla \log p_{0t} (x_t \vert x_0) = \frac{x_t - \mu(t) x_0}{\sigma^2 (t)} = - \frac{z}{\sigma (t)} \\ x_t = \mu(t) x_0 + \sigma(t) z, \quad z \sim \mathcal{N}(0,I) \end{equation}\]를 민족한다. $\sigma (t)$는 $t \rightarrow 0$일 때 0으로 수렴하며,
\[\begin{equation} \| s_\theta (x_t, t) - \nabla \log p_{0t} (x_t \vert x_0) \|_2^2 \end{equation}\]은 발산하게 된다. 따라서 NCSN loss에 대한 몬테 카를로 추정은 높은 분산에서 작동하며, score network의 안정적인 학습을 방해한다. 실제로 이전 연구는 diffusion time 범위를 $[\tau, T]$로 잘랐다.
2. Variational Bound With Positive Truncation
Lemma 1. 임의의 $\tau \in [0, T]$에 대하여
\[\begin{aligned} \mathbb{E}_{x_\tau} [- \log p_\tau^\theta (x_\tau)] &\le \mathcal{L} (\theta; g^2, \tau) \\ &= \frac{1}{2} \int_\tau^T g^2 (t) \mathbb{E}_{x_0, x_t} [\| s_\theta (x_t, t) - \nabla \log p_{0t} (x_t \vert x_0) \|_2^2 ] dt \end{aligned}\]가 성립한다.
Lemma 1은 NCSN loss에 대한 부등식의 일반화이며, $\tau = 0$이면 둘이 같아진다. 만일 $\tau \in [0, T]$에 대하여 시간 범위가 $[\tau, T]$로 잘리면, log-likelihood는
\[\begin{equation} \mathbb{E}_{x_0} [- \log p_0^\theta (x_0)] \le \mathbb{E}_{x_\tau} [- \log p_\tau^\theta (x_\tau)] + R_\tau (\theta) \\ R_\tau (\theta) = \mathbb{E}_{x_0} \bigg[ \int p_{0 \tau} (x_\tau \vert x_0) \log \frac{p_{0 \tau} (x_\tau \vert x_0)}{p_\theta (x_0 \vert x_\tau)} dx_\tau \bigg] \end{equation}\]가 된다. 따라서 임의의 $\tau$에 대하여 위 부등식의 우변애 Lemma 1을 적용하면 log-likelihood의 variational bound를 다음과 같이 얻을 수 있다.
\[\begin{equation} \mathbb{E}_{x_0} [- \log p_0^\theta (x_0)] \le \mathcal{L} (\theta; g^2, \tau) + R_\tau (\theta) \end{equation}\]3. A Universal Phenomenon in Diffusion Training: Extremely Imbalanced Loss
발산하는 문제를 피하기 위해 VPSDE의 이전 연구에서는 고정된 hyperparameter $\tau = \epsilon > 0$로 적분을 [\tau, T]로 잘라 loss를 수정하여 score network가 $[0, \epsilon)$에서 score 함수를 추정하지 않도록 하였다. 이와 유사하게 VESDE의 연구에서는
\[\begin{equation} \sigma_{VE}^2 (t) \approx \sigma_{min}^2 \bigg( \frac{\sigma_{max}}{\sigma_{min}} \bigg)^{2t} \end{equation}\]로 근사하여 전이 확률의 분산 최소값을 $\sigma_{min}^2$으로 자른다. 이는 VPSDE에서 diffusion time을 $\epsilon$으로 자르는 것과 동등하다. 따라서, 본 논문에서는 diffusion time을 자르는 것과 diffusion 분산을 자르는 것을 교환 가능하게 다룬다.
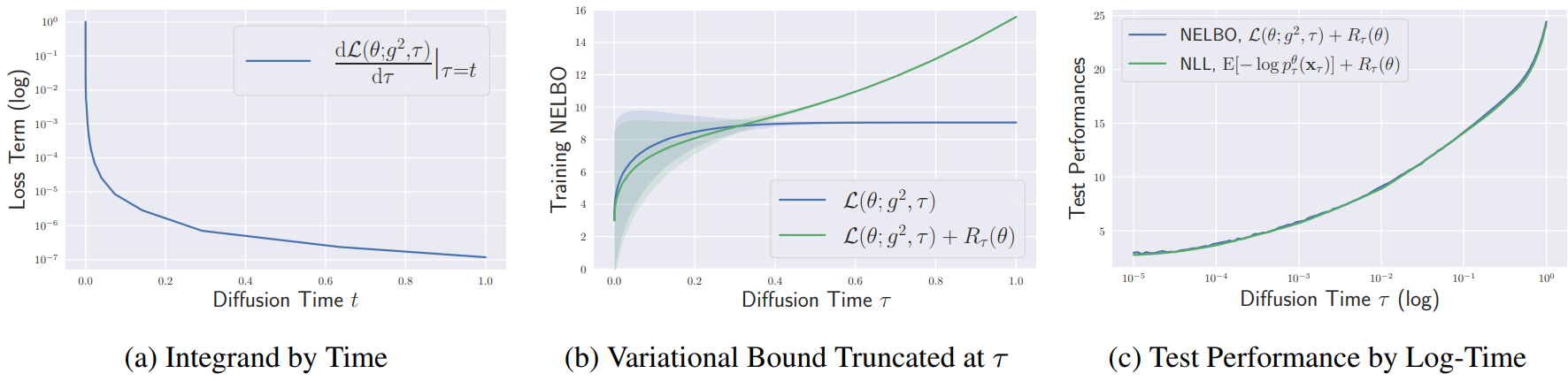
위 그래프는 diffusion model의 학습에서 truncation의 중요성을 보여준다. 그래프 (a)는 $\epsilon = 10^{-5}$으로 자른 것으로, Bits-Per-Dimension (BPD) scale에서 $\mathcal{L} (\theta; g^2, \tau)$의 피적분함수가 여전히 굉장히 불균형함을 보여준다. 이러한 극심한 불균형은 diffusion model 학습에서 보편적인 현상으로 나타나며, 이러한 현상은 학습 시작부터 끝까지 지속된다.
그래프 (b)에서 초록색 선은 log-likelihood의 variational bound를 나타내며, 작은 diffusion time 근처에서 variational bound가 급격히 감소함을 보여준다. 따라서 $\epsilon$이 충분히 작지 않으면 variational bound가 log-likelihood에 엄격하지 않고 MLE 학습에서 diffsion model이 실패한다.
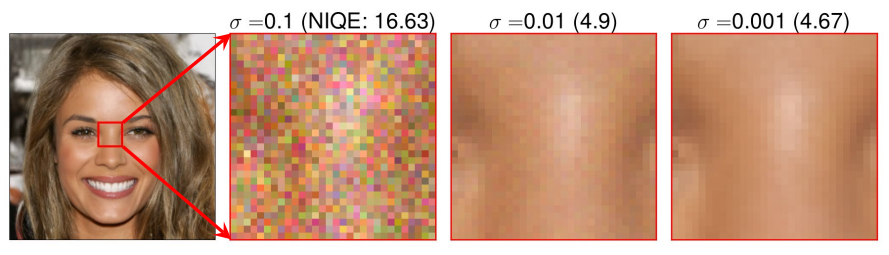
또한, 위 그림은 충분히 작지 않은 $\epsilon$(또는 $\sigma_{min}$)도 미세한 샘플 품질에 해를 끼칠 수 있음을 나타낸다. 따라서 $\epsilon$은 신중하게 선택해야 하는 중요한 hyperparameter이다.
4. Effect of Truncation on Model Evaluation
그래프 (c)는 밀도 추정에 대한 테스트 성능을 보여준다. $\epsilon$이 작아지면 Negative Evidence Lower Bound (NELBO)와 NLL 모두 단조 감소함을 보여주며, 이는 학습에서와 마찬가지로 테스트에서도 NELBO가 작은 diffusion time에 크게 기여되기 때문이다. 따라서 테스트 NELBO/NLL을 줄이기 위해 $\epsilon$을 최대한 줄이는 것이 일반적인 전략이 될 수 있다.
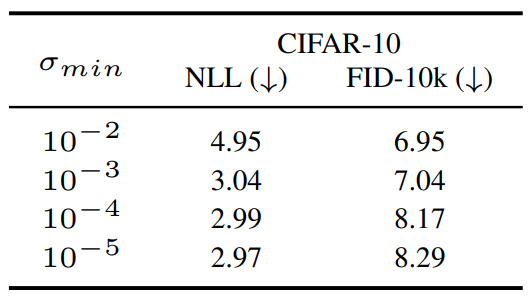
반대로, 위 표는 학습 중에 $\sigma_{min}$이 작아지면 FID가 증가하는 것을 보여준다. 그래프 (b)의 파란색 선에서 variational bound에 크게 기여하는 것은 작은 diffusion time의 범위이므로 작은 truncation hyperparameter가 있는 score network는 큰 diffusion time에서 최적화되지 않은 상태로 유지된다. 따라서 위 표의 일관되지 않은 결과는 큰 diffusion time에 대한 부정확한 score에 기인한다.
저자들은 이를 확인하기 위해 실험을 디자인하였다. 이 실험은 2가지 종류의 score network를 사용한다. \(\sigma_{min} \in \{10^{-3}, 10^{-4}, 10^{-5}\}\)으로 각각 학습된 대체 네트워크로 $\sigma_{max}$에서 $\sigma_{tr} (= 1)$까지 denoise한 다음, $\sigma_{min} = 10^{-5}$으로 학습된 추가 네트워크로 $\sigma_{tr}$에서 $\sigma_{min} = 10^{-5}$까지 denoise한다. 이를 통해 큰 diffusion time에서의 score 정확도를 비교할 수 있게 된다. 실험 결과는 아래 표와 같다.
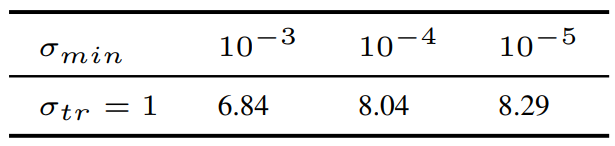
$\sigma_{min} = 10^{-3}$로 학습된 모델이 가장 좋은 FID를 보였으며, 이는 너무 작은 truncation은 샘플 품질에 해가 된다는 것을 보여준다.
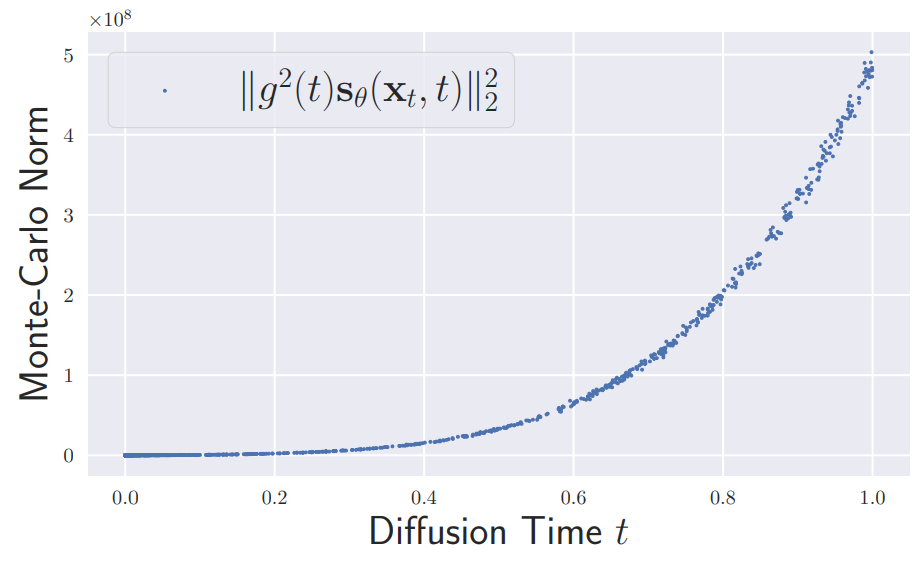
구체적으로, 위 그래프는 생성 프로세스의 drift 항인 $g^2 (t) s_\theta (x_t, t)$의 Euclidean norm을 보여주며, 큰 diffusion timte이 샘플링 프로세스를 지배한다는 것을 보여준다. 따라서, 큰 diffsion time에 대한 정밀한 score 네트워크는 샘플 생성에 특히 중요하다.
부정확한 score는 주로 글로벌한 샘플 컨텍스트에 영향을 미치며, 이는 작은 diffusion time에 대한 denoising은 미세한 디테일로만 이미지를 만들기 때문이다.

위 그림은 글로벌한 fidelity가 어떻게 손상되는지 보여준다. 두 번째 행에서 합성된 남자 이미지는 큰 diffusion time에서 이마에 비현실적인 곱슬 머리가 생긴다.

위 그림은 큰 diffusion time에 대한 좋은 score 추정 학습의 중요성을 보여준다. $x_\tau$에서 시작하여 생성 프로세스를 reverse-time으로 풀어 재생성된 샘플을 보여준다.
Soft Truncation: A Training Technique for a Diffusion Model
1. Monte-Carlo Estimation of Truncated Variational Bound with Importance Sampling
먼저 truncation hyperparameter를 $\tau = \epsilon$로 고정한 경우에 대해 다룬다. 모든 batch \(\{x_0^{(b)}\}_{b=1}^B\)에 대하여 variational bound의 몬테 카를로 추정은 다음과 같다.
\[\begin{aligned} \mathcal{L} (\theta; g^2, \epsilon) & \approx \hat{\mathcal{L}} (\theta; g^2, \epsilon) \\ &= \frac{1}{2B} \sum_{b=1}^B g^2 (t^{(b)}) \| s_\theta (x_{t^{(b)}}, t^{(b)}) - \nabla \log p_{0 t^{(b)}} (x_{t^{(b)}} \vert x_0) \|_2^2 \end{aligned}\]몬테 카를로 추정에서는 linear SDE하에서 전이 확률이
\[\begin{equation} \nabla \log p_{0 t^{(b)}} (x_{t^{(b)}} \vert x_0) = \frac{\epsilon^{(b)}}{\sigma(t^{(b)})} \end{equation}\]와 같은 수치적 형태로 tractable하게 계산 가능하다.
이전 연구에서는 중요도 확률이
\[\begin{equation} p_{iw} (t) = \frac{g^2 (t) / \sigma^2 (t)}{Z_\epsilon} 1_{[\epsilon, T]} (t), \quad Z_\epsilon = \int_\epsilon^T \frac{g^2 (t)}{\sigma^2 (t)} dt \end{equation}\]인 중요도 샘플랑울 적용하였다. 하지만 각 학습 iteration에서
\[\begin{equation} p_{iw}^\ast (t) \approx g^2 (t) L(t) \\ L(t) = \mathbb{E}_{x_0, x_t} [\| s_\theta (x_t, t) - \nabla \log p_{0t} (x_t \vert x_0) \|_2^2 ] \end{equation}\]으로부터 몬테 카를로 diffusion time을 샘플링하면 중요도 샘플링에 score 평가가 필요하기 때문에 학습 속도가 2배 느려진다. 따라서 이전 연구에서는 $L(t)$를
\[\begin{equation} \hat{L} (t) = \mathbb{E}_{x_0, x_t} [\| \nabla \log p_{0t} (x_t \vert x_0) \|_2^2 ] \approx 1 / \sigma^2(t) \end{equation}\]으로 근사하고 $p_{iw} (t)$를 중요도 가중치의 근사값으로 사용한다. 이 근사는 inverse Cumulative Distribution Function (CDF)의 closed-form이 잘 알려져 있기 때문에 계산 비용이 낮다. 분산을 직접 학습하지 않기 때문에 학습 속도 측면에서 $p_{iw} (t)$가 최대로 효율적인 sampler이다. 중요도로 가중된 몬테-카를로 추정은 다음과 같다.
\[\begin{aligned} \mathcal{L} (\theta; g^2, \epsilon) &= \frac{Z_\epsilon}{2} \int_\epsilon^T p_{iw} (t) \sigma^2 (t) \mathbb{E} [\| s_\theta (x_t, t) - \nabla \log p_{0t} (x_t \vert x_0) \|_2^2 ] dt \\ & \approx \frac{Z_\epsilon}{2B} \sum_{b=1}^B \sigma^2 (t_{iw}^{(b)}) \bigg\| s_\theta (x_{t_{iw}^{(b)}}, t_{iw}^{(b)}) - \frac{\epsilon^{(b)}}{\sigma (t_{iw}^{(b)})} \bigg\|_2^2 \\ & := \hat{L}_{iw} (\theta; g^2, \epsilon) \end{aligned}\]\(\{t_{iw}^{(b)}\}_{b=1}^B\)는 중요도 분포에서 샘플링한 몬테 카를로 샘플이다.
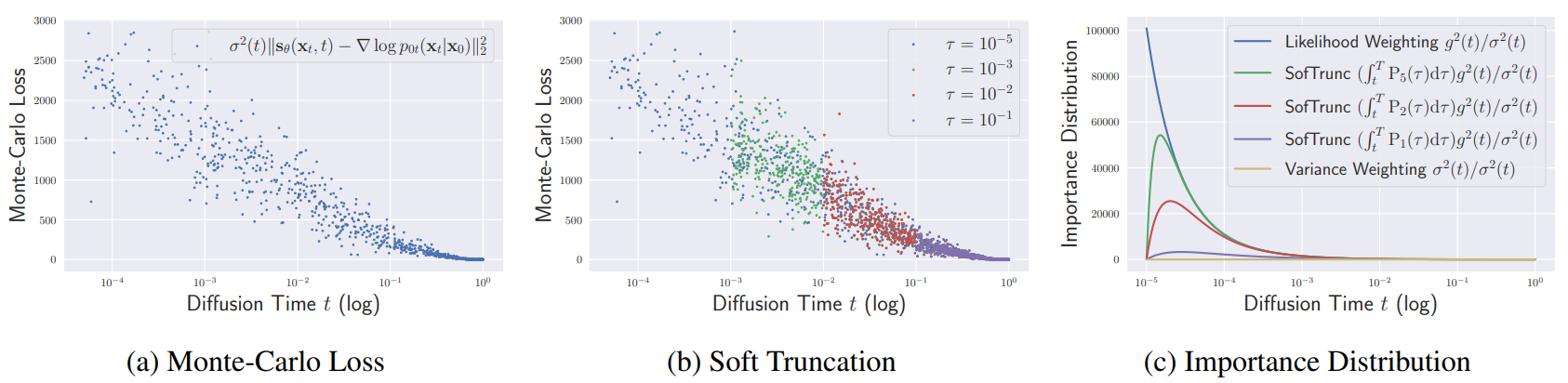
중요도 샘플링은 추정 분산을 상당히 낮추기 때문에 중요도 샘플링은 NLL과 FID 모두에서 균등 샘플링보다 좋다. 위의 그래프 (a)는 샘플별 loss를 나타낸 것이며, 중요도 샘플링은 diffusion time에 따라 loss를 크게 완화한다. 하지만 그래프 (c)에서 $t \rightarrow 0$으로 가면 중요도 분포 $p_{iw} (t)$가 발산하는 것을 볼 수 있다.

또한 위 그림에서 보면 중요도로 가중된 몬테 카를로 시간의 대부분이 $t \approx \epsilon$에 집중된다. 따라서 중요도 샘플링의 사용은 분산 감소와 $t \approx \epsilon$ 근처에서 오버 샘플링되는 것 사이의 trade-off를 가진다. 따라서 중요도 샘플링의 사용 여부와 관계없이 큰 diffusion time에 대한 부정확한 score 추정은 샘플링 전략에 독립적으로 나타나며, 이러한 조기 score 추정을 해결하는 것은 중요한 task가 된다.
Likelihood weighting 대신에 이전 연구들은 denoising score loss를 variance weighting $\lambda(t) = \sigma^2 (t)$로 학습하였다. 이 weighting으로는 중요도 분포가 균등 분포가 된다.
\[\begin{equation} p_{iw} (t) = \frac{\lambda(t)}{\sigma^2 (t)} = 1 \end{equation}\]따라서 likelihood weighting을 사용할 때 나타나는 trade-off를 상당히 완화한다. 반면, variance weighting은 FID를 선호하고 NLL을 희생한다. 이는 loss가 더 이상 log-likelihood의 variational bound이 아니기 때문이다. 반대로 likelihood weighting을 사용한 학습은 FID보다 NLL에 대해 학습된다. 따라서 Soft Truncation은 NLL과 FID의 균형을 위해 likelihood weighting을 사용한다.
2. Soft Truncation
Soft Truncation은 trucation hyperparameter를 정적 변수가 아닌 확률 분포 $\mathbb{P}(\tau)$를 따르는 확률 변수로 둔다. 모든 mini-batch 업데이트에서 Soft Truncation은 샘플링된 $\tau \sim \mathbb{P} (\tau)$를 사용하여 diffusion model을 최적화한다. Soft Truncation은 중요도 분포
\[\begin{equation} p_{iw, \tau} (t) = \frac{g^2 (t) / \sigma^2 (t)}{Z_\tau} 1_{[\tau, T]} (t), \quad Z_\tau = \int_\tau^T \frac{g^2 (t)}{\sigma^2 (t)} dt \end{equation}\]에서 \(\{t_{iw}^{(b)}\}_{b=1}^B\)를 샘플링하여 몬테 카를로 loss
\[\begin{equation} \hat{\mathcal{L}}_{iw} (\theta; \lambda, \tau) = \frac{Z_\tau}{2B} \sum_{b=1}^B \sigma^2 (t_{iw}^{(b)}) \bigg\| s_\theta (x_{t_{iw}^{(b)}}) - \frac{\epsilon^{(b)}}{\sigma (t_{iw}^{(b)})} \bigg\|_2^2 \end{equation}\]를 최적화한다.
Soft Truncation은 $t \approx \epsilon$ 근처에서 diffusion time이 오버 샘플링되는 문제를 해결하며, 이는 몬테 카를로 time이 $\epsilon$에 더 이상 집중되지 않는다. $[\tau, T]$로 제한된 범위는 score network가 diffusion time에 대해 더 균형있게 학습할 기회를 제공한다.
3. Soft Truncation Equals to A Diffusion Model With A General Weigh
원래 diffsion model에서 loss의 추정 $\hat{\mathcal{L}} (\theta; g^2, \epsilon)$은 $\mathcal{L} (\theta; g^2, \epsilon)$의 batch-wise 근사일 뿐이다. 하지만 target loss $\mathcal{L} (\theta; g^2, \tau)$는 $\tau$에 의존하므로 이 loss 자체가 확률 변수이다. 따라서 저자들은 Soft Truncation loss의 기대값을 유도하여 원래 diffsion model과의 연결을 보였다.
\[\begin{aligned} \mathcal{L}_{ST} (\theta; g^2, \mathbb{P}) & := \mathbb{E}_{\mathbb{P} (\tau)} [\mathcal{L} (\theta; g^2, \tau)] \\ &= \frac{1}{2} \int_\epsilon^T \mathbb{P} (\tau) \int_\tau^T g^2 (t) \mathbb{E} [\| s_\theta - \nabla \log p_{0t} \|_2^2] dt d \tau \\ &= \frac{1}{2} \int_\epsilon^T g_{\mathbb{P}}^2 (t) \mathbb{E} [ \| s_\theta - \nabla \log p_{0t} \|_2^2 ] dt \end{aligned}\]여기서
\[\begin{equation} g_{\mathbb{P}}^2 (t) = (\int_0^t \mathbb{P} (\tau) d \tau) g^2 (t) \end{equation}\]이다. 따라서 Soft Truncation은 $g_{\mathbb{P}}^2 (t)$의 일반적인 가중치로 diffsion model을 줄인다.
\[\begin{equation} \mathcal{L}_{ST} (\theta; g^2, \mathbb{P}) = \mathcal{L} (\theta; g_\mathbb{P}^2 (t), \epsilon) \end{equation}\]4. Soft Truncation is Maximum Perturbed Likelihood Estimation
앞서 Soft Truncation이 기대값 관점에서 일반적인 가중치를 가지는 diffsion model임을 설명하였다. 역으로, 일반적인 가중치를 가지는 diffsion model을 Soft Truncation 관점에서 분석할 수 있다.
Theorem 1. $\lambda(t) / g^2 (t)$가 $[\epsilon, T]$에서 감소하지 않는 음이 아닌 연속 함수이고 $[0, \epsilon)$에서 0이라고 가정하자.
\[\begin{equation} \mathbb{P}_\lambda ([a, b]) = \frac{1}{Z} \bigg[ \int_{\max (a, \epsilon)}^b \bigg( \frac{\lambda(s)}{g^2 (s)} \bigg)' ds + \frac{\lambda (\epsilon)}{g^2 (\epsilon)} 1_{[a,b]} (\epsilon) \bigg] \\ Z = \frac{\lambda (T)}{g^2 (T)} \end{equation}\]로 정의되는 확률에 대하여 general weighted diffusion loss의 variational bound는
\[\begin{aligned} \mathbb{E}_{\mathbb{P}_\lambda (\tau)} [D_{KL} (p_\tau \vert p_\tau^\theta)] & \le \frac{1}{2Z} \int_\epsilon^T \lambda(t) \mathbb{E}_{x_t} [\| s_\theta (x_t, t) - \nabla \log p_t (x_t) \|_2^2 ] dt \\ &= \frac{1}{Z} \mathcal{L} (\theta; \lambda, \epsilon) = \mathbb{E}_{\mathbb{P}_\lambda (\tau)} [\mathcal{L} (\theta; g^2, \tau)] \end{aligned}\]가 된다.
Theorem 1의 관점에서 Soft Truncation의 뜻이 더 분명해진다. General weighted diffsion loss $\mathcal{L} (\theta; \lambda, \epsilon)$를 학습하는 대신 truncated variational bound $\mathcal{L} (\theta; g^2, \tau)$를 최적화한다. Lemma 1에 의해 이 truncated loss는 pertubed KL divergence $D_{KL} (p_\tau \vert p_\tau^\theta)$의 상한이다. 따라서 Soft Truncation은 Maximum Perturbed Likelihood Estimation (MPLE)로 해석될 수 있으며, pertubation level은 확률 변수이다. $\tau$가 충분히 작지 않으면 부등식
\[\begin{equation} \mathbb{E}_{x_0} [- \log p_0^\theta (x_0)] \le \mathcal{L} (\theta; g^2, \tau) + R_\tau (\theta) \end{equation}\]이 타이트하지 않으므로 Soft Truncation은 MLE 학습이 아니다.
안정적인 학습이 가능한 경우 loss의 분산을 최소화하는 것이 오래된 지혜다. 그러나 딥러닝의 일부 최적화 방법(ex. SGD)은 결국 local optimum에서 벗어나는 데 도움이 되는 loss function에 의도적으로 noise를 추가한다. Soft Truncation은 loss 추정에 의도적으로 보조 임의성을 부과하여 loss의 분산을 부풀리는 최적화 방법으로 분류된다. 이 랜덤성은 diffusion time을 batch-wise하게 제어하는 \(\mathbb{E}_{\mathbb{P}_\lambda (\tau)}\)의 outmost expectation으로 표시된다. 또한 샘플링된 $\tau$의 loss는 $\tau$에 의한 pertubed KL divergence의 proxy(대리)이므로 loss 추정에 대한 보조 랜덤성은 랜덤 pertubation이 아님을 의미한다.
5. Choice of Truncation Probability Distribution
본 논문은 $\tau$의 확률 분포를 충분히 작은 truncation hyperparameter를 사용하여 다음과 같이 parameterize한다.
\[\begin{equation} \mathbb{P}_k (\tau) = \frac{1 / \tau^k}{Z_k} 1_{[\epsilon, T]} (\tau) \approx \frac{1}{\tau^k} \\ Z_k = \int_\epsilon^T \frac{1}{\tau^k} d \tau \end{equation}\]$\tau \approx 0 < \epsilon$으로 batch 업데이트하는 것이 score network를 최적점에서 멀리 보내므로 $\epsilon$을 고정하는 것이 여전히 좋다. 위 식의 정의에서 $k$가 무한으로 가면 $\mathbb{P}_k (\tau)$도 무한으로 가며, 이 델타 분포는 likelihood weighting을 사용하는 원래 diffsion model에 해당한다.
이 간단한 형태를 사용하였을 때, 저자들은 VPSDE에서 $k \approx 1.0$, VESDE에서 $k = 2.0$이 샘플 품질을 극대화하는 지점이라는 것을 실험을 통해 찾았다. VPSDE의 경우 $k \approx 1.0$이면 중요 분포가 variance weighting에 가까워져서 낮은 NLL을 유지하면서 샘플 품질이 개선된다. 반면에, $k$가 너무 작으면 $\epsilon$ 근처에서 $\tau$가 샘플링되지 않으므로 샘플 생성과 밀도 추정에 모두 나빠진다.
Experiments
- 데이터셋: CIFAR-10, ImageNet 32$\times$32, STL-10, CelebA 64$\times$64, CelebA-HQ 256$\times$256
- 아키텍처: vanilla NCSN++, DDPM++, Unbounded NCSN++ (UNCSN++), Unbounded DDPM++ (UDDPM++)
- SDE: VESDE, VPSDE, Reverse VESDE (RVESDE)
FID by Iteration
다음은 학습 step에 대한 FID를 나타낸 그래프이다.

15만 iteration 이후 Soft Truncation이 일반 학습 방법을 이긴다.
Ablation Studies
다음은 다양한 weighting에 대한 ablation study 결과이다. (CIFAR-10 & ImageNet32 / DDPM++ (VP))
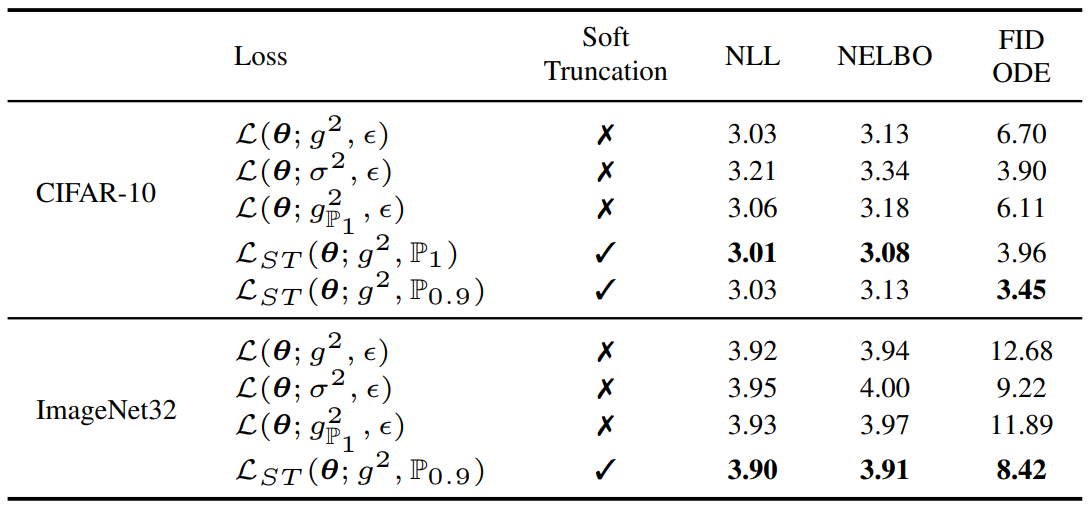
다음은 다양한 모델 아키텍처와 다양한 SDE에 대한 ablation study 결과이다. (CelebA)
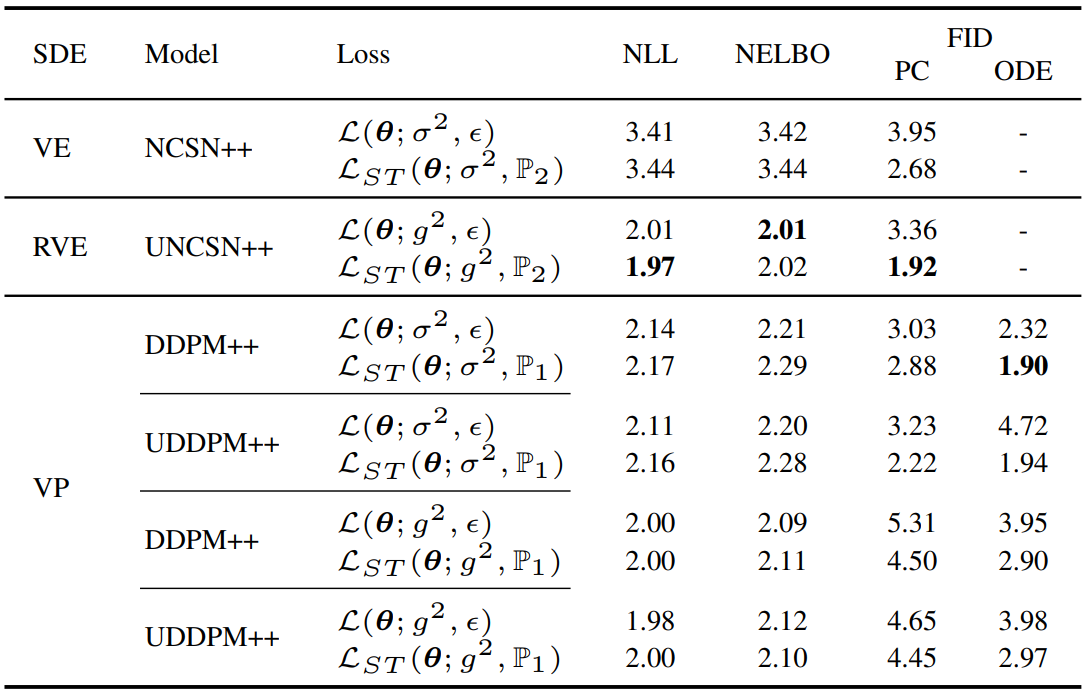
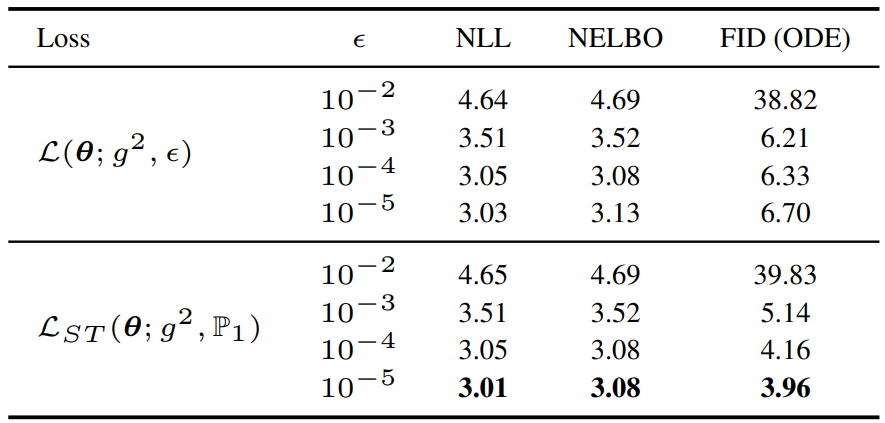
다음은 다양한 $\epsilon$에 대한 ablation study 결과이다. (CIFAR-10 / DDPM++ (VP))
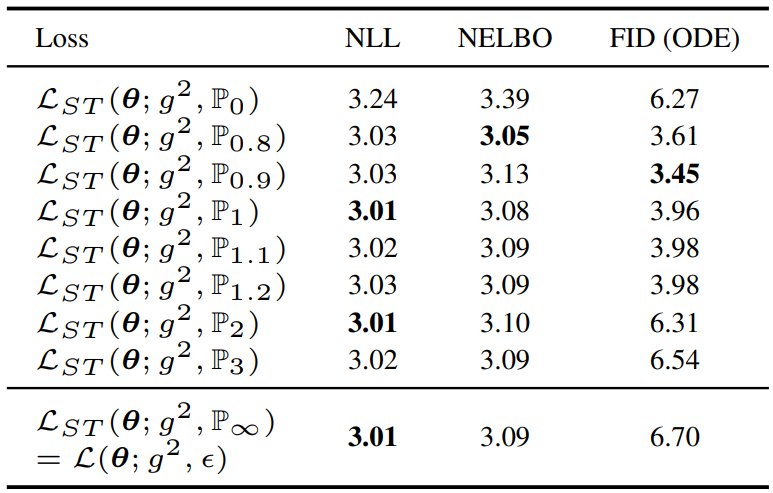
다음은 다양한 $\mathbb{P}_k$에 대한 ablation study 결과이다. (CIFAR-10 / DDPM++ (VP))
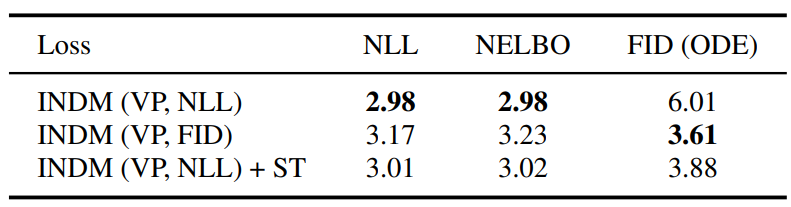
다음은 diffusion을 INDM의 normalizing flow와 결합하였을 때의 ablation study 결과이다. (CIFAR-10 / DDPM++ (VP))
Quantitative Comparison to SOTA
다음은 다양한 데이터셋에 대한 성능 비교 결과이다.








![[Paper review] Self-correcting LLM-controlled Diffusion Models](/assets/images/blog/post-5.jpg)