Blogs

arXiv 2022. [Paper] [Github]
Ben Poole, Ajay Jain, Jonathan T. Barron, Ben Mildenhall
Google Research | UC Berkeley
29 Sep 2022

Introduction

텍스트 기반 이미지 생성 모델은 fidelity가 높고 다양하며 제어 가능한 이미지 합성을 지원한다. 이러한 품질 향상은 대규모로 정렬된 이미지-텍스트 데이터셋과 확장 가능한 생성 모델 아키텍처에서 비롯되었다. Diffusion model은 안정적이고 확장 가능한 denoising 목적 함수로 고품질 이미지 generator를 학습하는 데 특히 효과적이다. Diffusion model을 다른 양식에 적용하는 것은 성공적이었지만 많은 양의 양식별로 학습 데이터가 필요하다. 본 논문에서는 사전 학습된 2D 이미지-텍스트 diffusion model을 3D 데이터 없이 3D 객체 합성으로 transfer하는 기술을 개발한다 (위 그림 참고). 2D 이미지 생성은 광범위하게 적용할 수 있지만 시뮬레이터나 비디오 게임, 영화와 같은 디지털 미디어는 풍부하게 환경을 채우기 위해 수천 개의 상세한 3D 에셋이 필요하다. 3D 에셋은 현재 Blender나 Maya3D와 같은 모델링 소프트웨어에서 수작업으로 설계되며, 이 프로세스에는 많은 시간과 전문 지식이 필요하다. Text-to-3D 생성 모델은 초보자의 진입 장벽을 낮추고 숙련된 아티스트의 작업 흐름을 개선할 수 있다.

3D 생성 모델은 voxel이나 point cloud와 같은 구조의 명시적 표현에서 학습될 수 있지만, 필요한 3D 데이터는 풍부한 2D 이미지에 비해 상대적으로 부족하다. 본 논문의 접근 방식은 이미지에 대해 학습된 2D diffusion model만 사용하여 3D 구조를 학습하고 이 문제를 피한다. GAN은 출력 3D 개체 또는 scene의 2D 이미지 렌더링에 적대적 loss를 배치하여 단일 개체의 사진에서 제어 가능한 3D generator를 학습할 수 있다. 이러한 접근 방식은 얼굴과 같은 특정 개체 범주에 대해 유망한 결과를 낳았지만 아직 임의의 텍스트를 지원하는 지 입증되지는 않았다.

Neural Radiance Fields (NeRF)는 volumetric raytracer가 공간 좌표에서 색상과 체적 밀도로의 neural mapping과 결합되는 inverse rendering에 대한 접근 방식이다. NeRF는 neural inverse rendering을 위한 중요한 도구가 되었다. 원래 NeRF는 “고전적인” 3D 재구성 task에 잘 작동하는 것으로 밝혀졌다. Scene의 많은 이미지가 모델에 대한 입력으로 제공되고 NeRF는 특정 scene의 geometry를 복구하도록 최적화되어 관찰되지 않은 각도에서 합성할 scene에 대한 새로운 view를 생성한다.

많은 3D 생성 접근 방식은 NeRF와 같은 모델을 더 큰 생성 시스템 내의 구성 요소로 통합하는 데 성공했다. 이러한 접근 방식 중 하나는 Dream Fields로, CLIP의 고정 이미지-텍스트 결합 임베딩 모델과 최적화 기반 접근 방식을 사용하여 NeRF를 학습시킨다. 이 연구는 사전 학습된 2D 이미지-텍스트 모델이 3D 합성에 사용될 수 있음을 보여주었지만, 이 접근 방식으로 생성된 3D 개체는 현실감과 정확성이 부족한 경향이 있다. CLIP은 voxel grid 및 mesh를 기반으로 하는 다른 접근 방식을 guide하는 데 사용되었다.

본 논문은 Dream Fields와 유사한 접근 방식을 채택하지만 CLIP을 2D diffusion model의 distillation에서 파생된 loss로 대체한다. 본 논문의 loss는 확률 밀도 distillation를 기반으로 하며, diffusion의 forward process를 기반의 공유된 평균을 가지는 가우시안 분포 계열과 사전 학습된 diffusion model에서 학습한 score function 사이의 KL divergence를 최소화한다. Score Distillation Sampling (SDS) 방법은 미분 가능한 이미지 parameterization에서의 최적화를 통해 샘플링이 가능하다. 이 3D 생성 task에 맞게 조정된 NeRF와 SDS를 결합함으로써 DreamFusion은 다양한 텍스트 프롬프트에 대해 fidelity가 높은 일관된 3D 개체 및 scene을 생성한다.

Diffusion Models and Score Distillation Sampling

Diffusion model은 tractable한 noise 분포에서 데이터 분포로 점진적으로 샘플을 변환하도록 학습된 모델이다. Diffusion model은 noise를 더해 데이터 $x$에서 천천히 구조를 제거하는 forward process $q$와 noise $z_t$에 천천히 구조를 더하는 reverse process로 구성된다. Forward process는 일반적으로 timestep $t$의 덜 noisy한 latent에서 $t+1$의 더 noisy한 latent로의 transition인 가우시안 분포이다. 데이터 $x$가 주어지면 latent의 주변 분포는 중간 timestep을 적분하여 구할 수 있다.

\[\begin{equation} q(z_t) = \int q(z_t \vert x) q(x) dx \\ q(z_t \vert x) = \mathcal{N} (\alpha_t x, \sigma_t^2 I) \end{equation}\]

$q(z_0)$은 데이터 분포에 가깝고 $q(z_T)$는 가우시안에 가깝도록 $\alpha_t$와 $\sigma_t$가 선택되며, $\alpha_t^2 = 1-\sigma_t^2$로 선택하여 분산이 보존되도록 한다.

생성 모델 $p$는 random noise $p(z_T) = \mathcal{N}(0,I)$에서 시작하여 transition $p_\phi (z_{t-1} \vert z_t)$로 천천히 구조를 더하도록 학습된다. 이론적으로 충분한 timestep이 있으면 최적의 reverse process도 가우시안이다. Transition은 일반적으로 다음과 같이 parameterize된다.

\[\begin{equation} p_\phi (z_{t-1} \vert z_t) = q(z_{t-1} \vert z_t, x = \hat{x}_\phi (z_t; t)) \end{equation}\]

$q(z_{t-1} \vert z_t, x)$는 사후 확률 분포이다. 직접 \(\hat{x}_\phi\)를 예측하는 대신 DDPM에서는 $z_t$의 noise 성분을 예측하는 U-Net $\epsilon_\phi (z_t; t)$를 학습시킨다.

\[\begin{equation} \mathbb{E} [x \vert z_t] \approx \hat{x}_\phi (z_t; t) = \frac{z_t - \sigma_t \epsilon_\phi (z_t; t)}{\alpha_t} \end{equation}\]

예측된 noise는 예측된 score function과 연관된다.

Evidence lower bound (ELBO)로 생성 모델을 학습시키는 것은 다음과 같은 denoising score matching 목적 함수로 간단하게 만들 수 있다.

\[\begin{equation} \mathcal{L}_\textrm{Diff} (\phi, x) = \mathbb{E}_{t \sim \mathcal{U}(0, 1), \epsilon \sim \mathcal{N}(0,I)} [w(t) \|\epsilon_\phi (\alpha_t x + \sigma_t \epsilon; t) - \epsilon \|_2^2] \end{equation}\]

$w(t)$는 가중치 함수이다. Diffusion model의 학습은 latent 변수 모델을 학습하는 것 또는 noisy한 데이터의 score function을 학습하는 것으로 볼 수 있다. 본 논문에서는 score function이 $s_\phi (z_t; t) = - \epsilon_\phi (z_t; t) / \sigma_t$로 주어진 주변 분포의 근사값을 $p_\phi (z_t; t)$로 표기한다.

본 논문은 텍스트 임베딩 $y$로 컨디셔닝된 text-to-image diffusion model을 기반으로 한다. 이 모델은 unconditional model과 함께 학습하는 classifier-free guidance (CFG)를 사용한다.

\[\begin{equation} \hat{\epsilon}_\phi (z_t; y, t) = (1 + \omega) \epsilon_\phi (z_t; y, t) - \omega \epsilon_\phi (z_t; t) \end{equation}\]

$\omega$는 guidance scale parameter이다. CFG는 score function을 conditional 밀도와 unconditional 밀도의 비가 큰 영역으로 대체한다. 실제로 $\omega > 0$으로 두면 다양성이 감소하지만 샘플의 품질이 개선된다. Guide된 버전의 noise 예측과 주변 분포를 $\hat{\epsilon}$와 $\hat{p}$로 표기한다.

1. How can we sample in parameter space, not pixel space?

Diffusion model에서 샘플링하기 위한 기존 접근 방식은 유형과 차원이 모델이 학습된 데이터와 동일한 샘플을 생성한다. 조건부 diffusion sampling은 약간의 유연성(ex. inpainting)을 가능하게 하지만 픽셀에 대해 학습된 diffusion model은 전통적으로 픽셀만 샘플링하는 데 사용되었다. 본 논문은 픽셀 샘플링에 관심이 없다. 대신 임의의 각도에서 렌더링할 때 좋은 이미지처럼 보이는 3D 모델을 만들고 싶다. 이러한 모델은 differentiable image parameterization(DIP)로 세분화될 수 있으며, 여기서 미분 가능한 generator $g$는 이미지 $x = g(\theta)$를 생성하기 위해 매개변수 $\theta$를 변환한다. DIP를 사용하면 제약 조건을 표현하거나 보다 작은 공간에서 최적화하거나 픽셀 공간을 위한 보다 강력한 최적화 알고리즘을 활용할 수 있다. 3D의 경우 $\theta$를 3D volume의 파라미터로, $g$를 volumetric renderer로 지정한다. 이러한 파라미터를 학습하려면 diffusion model에 적용할 수 있는 loss function이 필요하다.

본 논문의 접근 방식은 diffusion model의 구조를 활용하여 최적화를 통해 tractable한 샘플링을 가능하게 한다. $x = g(\theta)$가 freeze된 diffusion model의 샘플처럼 보이도록 파라미터 $\theta$에 대해 최적화한다. 이 최적화를 수행하려면 DeepDream과 유사한 스타일로 그럴듯한 이미지는 loss가 적고 믿기지 않는 이미지는 loss가 높은 미분 가능한 loss function이 필요하다.

저자들은 먼저 학습된 조건부 밀도 $p(x \vert y)$의 모드를 찾기 위해 \(\mathcal{L}_\textrm{diff}\)를 재사용하는 방법을 조사했다. 고차원의 생성 모델 모드는 일반적인 샘플과 거리가 먼 경우가 많지만, diffusion model 학습의 멀티스케일 특성은 이러한 문제를 피하는 데 도움이 될 수 있다. 생성된 데이터 포인트 $x = g(\theta)$에 대한 \(\mathcal{L}_\textrm{diff}\)를 최소화하면

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \mathcal{L}_\textrm{diff} (\phi, x = g(\theta)) \end{equation}\]

가 된다. 실제로 이 loss function이 $x = \theta$인 항등 DIP를 사용하는 경우에도 실제 샘플을 생성하지 않는다는 것을 발견했다. 다른 연구에서는 이 방법이 신중하게 선택한 timestep schedule과 함께 작동하도록 만들 수 있음을 보여주지만, 이 목적 함수가 다루기 어렵고 timestep schedule이 조정하기 어렵다는 것을 발견했다.

이 방법의 어려움을 이해하기 위해 \(\mathcal{L}_\textrm{diff}\)의 기울기

\[\begin{equation} \nabla_\theta \mathcal{L}_\textrm{diff} (\phi, x = g(\theta)) = \mathbb{E}_{t, \epsilon} \bigg[ w(t) \underbrace{(\hat{\epsilon}_\phi (z_t; y, t) - \epsilon)}_{\textrm{Noise Residual}} \underbrace{\frac{\partial \hat{\epsilon}_\phi (z_t; y, t)}{\partial z_t}}_{\textrm{U-Net Jacobian}} \underbrace{\frac{\partial x}{\partial \theta}}_{\textrm{Generator Jacobian}} \bigg] \end{equation}\]

를 생각해보자. 실제로 U-Net Jacobian 항은 계산하는 데 비용이 많이 들고 (diffusion model U-Net을 통과하는 역전파가 필요) 주변 밀도의 스케일링된 Hessian에 근사하도록 학습되기 때문에 작은 noise level에 대해 컨디셔닝이 좋지 않다. 저자들은 U-Net Jacobian 항을 생략하면 diffusion model로 DIP를 최적화하기 위한 효과적인 기울기가 생성됨을 발견했다.

\[\begin{equation} \nabla_\theta \mathcal{L}_\textrm{diff} (\phi, x = g(\theta)) := \mathbb{E}_{t, \epsilon} \bigg[ w(t) (\hat{\epsilon}_\phi (z_t; y, t) - \epsilon) \frac{\partial x}{\partial \theta} \bigg] \end{equation}\]

직관적으로 이 loss는 $t$에 따라 $x$를 랜덤한 양의 noise로 손상시키며, 높은 밀도 영역으로 이동하기 위해 diffusion model의 score fuction을 따르는 업데이트된 방향을 추정한다. Diffusion model을 사용하여 DIP를 학습하기 위한 이 기울기는 diffusion model의 학습된 score fuction을 사용하는 가중 probability density distillation loss의 기울기임을 보여준다.

\[\begin{equation} \nabla_\theta \mathcal{L}_\textrm{SDS} (\phi, x = g(\theta)) = \nabla_\theta \mathbb{E}_t \bigg[\frac{\sigma_t}{\alpha_t} w(t) \textrm{KL} (q(z_t \vert g(\theta); y, t) \| p_\phi (z_t; y, t)) \bigg] \end{equation}\]

이 샘플링 접근 방식이 distillation과 연관이 있기 때문에 Score Distillation Sampling (SDS)이라 부르며, distillation에서 밀도 대신 score fuction이 사용되었다고 생각할 수 있다. $t \rightarrow 0$일 때 $q(z_t \vert \cdots)$의 noise가 사라지고 $g(\theta)$의 평균 파라미터가 원하는 샘플이 되므로 SDS를 sampler라고 부를 수 있다. Diffusion model이 업데이트 방향을 바로 예측하기 때문에 diffusion model에 역전파를 보낼 필요가 없으며, 모델은 효율적인 frozen critic과 같이 간단하게 행동한다.

\(\mathcal{L}_\textrm{SDS}\)의 모드 탐색 특성을 감안할 때 이 loss를 최소화하면 좋은 샘플이 생성되는지 여부가 불분명할 수 있다. 위 그림에서 SDS가 합리적인 품질의 제한된 이미지를 생성할 수 있음을 보여준다. 저자들은 경험적으로 classifier-free guidance의 guidance 가중치 $\omega$를 큰 값으로 설정하면 품질이 향상된다는 것을 발견했다. SDS는 ancestral sampling에 필적하는 디테일을 생성하지만 파라미터 공간에서 작동하기 때문에 새로운 전이 학습 (transfer learning) 애플리케이션이 가능하다.

The DreamFusion Algorithm

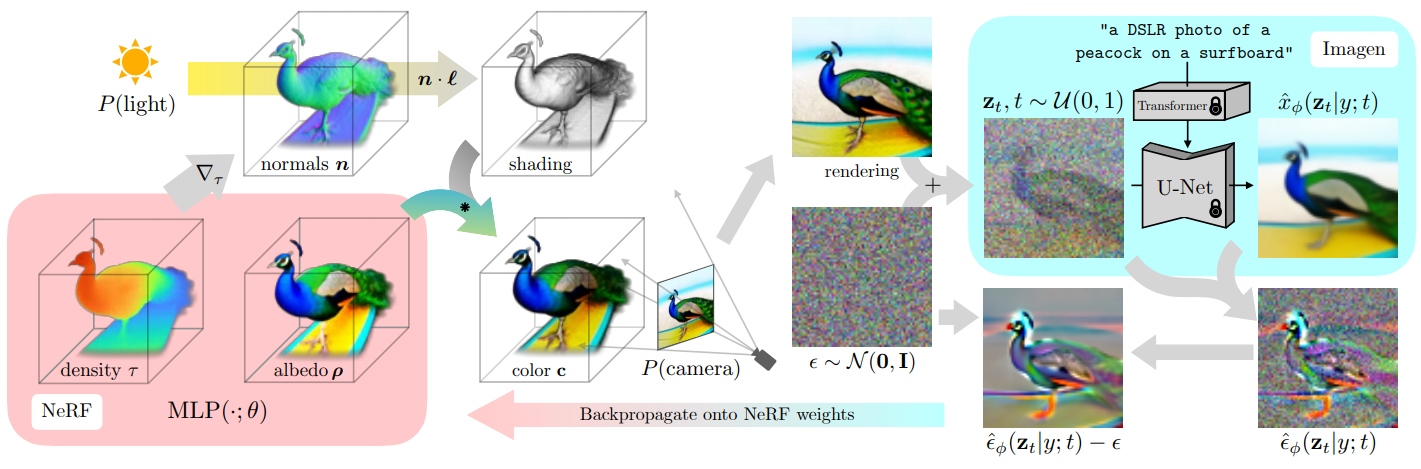
샘플을 생성하기 위해 일반적인 연속 최적화 문제 내에서 diffusion model을 loss로 사용할 수 있는 방법을 설명했으므로 이제 텍스트에서 3D 에셋을 생성할 수 있는 특정 알고리즘을 구성할 것이다. Diffusion model의 경우 텍스트에서 이미지를 합성하도록 학습된 Imagen 모델을 사용한다. 저자들은 64$\times$64 base model만 사용하고 이 사전 학습된 모델을 수정 없이 그대로 사용한다. 텍스트에서 scene을 합성하기 위해 NeRF와 유사한 모델을 임의의 가중치로 초기화한 다음 임의의 카메라 위치와 각도에서 해당 NeRF의 view를 반복적으로 렌더링한다. 이러한 렌더링을 Imagen을 감싸는 score distillation loss function에 대한 입력으로 사용한다. 이 접근 방식을 사용한 간단한 gradient descent은 결국 텍스트와 유사한 NeRF로 parameterize된 3D 모델을 생성한다. 이 접근 방식에 대한 개요는 위 그림과 같다.

1. Neural Rendering of a 3D Model

NeRF는 volumetric raytracer와 MLP로 구성된 neural inverse rendering 기술이다. NeRF에서 이미지를 렌더링하는 것은 카메라의 projection 중심에서 이미지 평면의 픽셀 위치로 각 픽셀에 대한 광선(ray)을 캐스팅하여 수행된다. 각 광선을 따라 샘플링된 3D 포인트 $\mu$는 MLP를 통과하여 4개의 스칼라 값을 출력으로 생성합니다.

1. Volumetric density $\tau$: 해당 3D 좌표에서 scene geometry의 불투명도
2. RGB 색상 $c$

이러한 밀도와 색상은 광선의 뒷면에서 카메라 방향으로 알파 합성(alpha-compositing)되어 픽셀에 대해 최종 렌더링된 RGB 값을 생성한다.

\[\begin{equation} C = \sum_i w_i c_i, \quad w_i = \alpha_i \prod_{j < i} (1 - \alpha_j), \quad \alpha_i = 1 - \exp (-\tau_i \| \mu_i - \mu_{i+1} \|) \end{equation}\]

기존의 NeRF 사용 사례에서는 입력 이미지와 관련 카메라 위치의 데이터셋이가 제공되며, NeRF MLP는 각 픽셀의 렌더링된 색상과 입력 이미지의 ground-truth 색상 사이의 MSE loss function을 사용하여 학습된다. 이렇게 하면 이전에 본 적이 없는 view에서 사실적인 렌더링을 생성할 수 있는 3D 모델(MLP의 가중치로 parameterize됨)이 생성된다. 본 논문의 모델은 앨리어싱을 줄이는 NeRF의 개선된 버전인 mip-NeRF 360을 기반으로 한다. 원래 Mip-NeRF 360은 이미지에서 3D 재구성을 위해 디자인되었지만 그 개선 사항은 text-to-3D 생성 task에도 도움이 된다.

Shading

기존의 NeRF 모델은 3D point가 관찰되는 광선 방향에 따라 조절되는 RGB 색상인 radiance를 방출한다. 대조적으로, 본 논문의 MLP는 표면 자체의 색상을 parameterize한 다음 제어할 수 있는 조명으로 비추며, 이는 일반적으로 “shading”이라고 하는 프로세스다. NeRF 같은 모델을 사용한 생성 또는 multiview 3D 재구성에 대한 이전 연구들은 다양한 반사율 모델(reflectance model)을 제안했다. 각 point에 대해 RGB 알베도 $\rho$ (재료의 색상)를 사용한다.

\[\begin{equation} (\tau, \rho) = \textrm{MLP} (\mu; \theta) \end{equation}\]

3D 포인트에 대한 최종 shading 출력 색상을 계산하려면 객체 geometry의 로컬 방향을 나타내는 법선 벡터가 필요하다. 이 표면 법선 벡터는 3D 좌표 $\mu$에 대한 밀도 $\tau$의 음의 기울기를 정규화하여 계산할 수 있다.

\[\begin{equation} n = - \frac{\nabla_\mu \tau}{\| \nabla_\mu \tau \|} \end{equation}\]

각 $n$과 재료의 알베도 $\rho$로, 3D 좌표 $l$과 색상 $l_\rho$, 주변광 색상 $l_a$를 갖는 일부 점 광원을 가정하고 diffuse reflectance을 사용하여 광선을 따라 각 점을 렌더링하여 각 점에 대한 색상 $c$를 생성한다.

\[\begin{equation} c = \rho \circ (l_\rho \circ \max (0, \frac{n \cdot (l - \mu)}{\| l - \mu \|}) + l_a) \end{equation}\]

위와 같이 계산된 색상과 이전에 생성한 밀도를 사용하여 표준 NeRF에서 사용되는 렌더링 가중치 $w_i$로 볼륨 렌더링 적분을 근사화한다. Text-to-3D 생성에 대한 이전 연구들에서는 $ρ$를 흰색 (1, 1, 1)으로 랜덤하게 대체하여 “textureless” shading 출력을 생성하는 것이 유익하다는 것을 알았다. 이렇게 하면 모델이 텍스트 컨디셔닝을 충족하기 위해 평면 geometry에 scene 콘텐츠를 그리는 저하된 솔루션을 생성하는 것을 방지할 수 있다. 예를 들어, 이 방법을 사용하면 다람쥐 이미지가 포함된 평평한 표면 대신 3D 다람쥐를 생성하도록 최적화를 장려한다. 둘 다 특정 view 각도와 조명 조건에서 동일하게 나타날 수 있다.

Scene Structure

본 논문의 방법은 일부 복잡한 scene을 생성할 수 있지만, 고정된 경계 구 내에서 NeRF scene 표현만 쿼리하고 위치 인코딩된 광선 방향을 입력으로 사용하는 두 번째 MLP에서 생성된 환경 맵으로 배경색을 생성하는 것이 도움이 된다는 것을 발견했다. 누적된 알파 값을 사용하여 이 배경색 위에 렌더링된 광선 색상을 합성한다. 이렇게 하면 NeRF 모델이 카메라에 매우 가까운 밀도로 공간을 채우는 것을 방지하면서 생성된 scene 뒤에 적절한 색상이나 배경을 칠할 수 있다. Scene 대신 단일 개체를 생성하는 경우 축소된 경계 구가 유용할 수 있다.

Geometry regularizers

본 논문에서 구축한 mip-NeRF 360 모델에는 간결성을 위해 생략한 많은 디테일이 포함되어 있다. Dream Field 논문과 유사하게 각 광선을 따라 불투명도에 정규화 페널티를 포함하여 불필요한 빈 공간 채우기를 방지한다. 법선 벡터가 카메라 반대쪽을 향하는 density field에서의 문제를 방지하기 위해 Ref-NeRF 논문에서 제안된 orientation loss의 수정된 버전을 사용한다. 이 페널티는 textureless shading을 포함할 때 중요하다. 그렇지 않으면 density field가 shading이 더 어두워지도록 법선을 카메라에서 멀어지게 하려고 시도하기 때문이다.

2. Text-to-3D synthesis

사전 학습된 text-to-image diffusion model, NeRF 형태의 미분 가능한 이미지 parameterization, 최소값이 좋은 샘플인 loss function이 주어지면 3D 데이터를 사용하지 않고 text-to-3D 합성에 필요한 모든 구성 요소를 갖는다. 각 텍스트 프롬프트에 대해 랜덤하게 초기화된 NeRF를 처음부터 학습시킨다. DreamFusion 최적화의 각 iteration은 다음을 수행한다.

1. 카메라와 조명을 랜덤하게 샘플링
2. 해당 카메라에서 NeRF의 이미지를 렌더링하고 조명으로 shading 처리
3. NeRF 파라미터에 대한 SDS loss의 기울기를 계산
4. Optimizer를 사용하여 NeRF 파라미터를 업데이트

1. Random camera and light sampling

각 iteration에서 카메라 위치는 구면좌표계에서 랜덤하게 샘플링되며, 앙각(elevation angle) $\phi_\textrm{cam}$, 방위각(azimuth angle) $\theta_\textrm{cam}$, 원점으로부터의 거리의 범위는 각각 $[-10^\circ, 90^\circ]$, $[0^\circ, 360^\circ]$, $[1, 1.5]$이다.

또한 원점 주변의 “look-at” point와 “up” vector를 샘플링하고 이를 카메라 위치와 결합하여 camera pose matrix를 만든다. Focal length(초점 거리)가 $\lambda_\textrm{focal} w$가 되도록 focal length multiplier $\lambda_\textrm{focal} \in \mathcal{U}(0.7, 1.35)$를 추가로 샘플링한다. 여기서 $w = 64$는 이미지 너비(픽셀)이다. 점 광원 위치 $l$은 카메라 위치를 중심으로 한 분포에서 샘플링된다. 다양한 카메라 위치를 사용하는 것이 일관된 3D scene을 합성하는 데 중요하며 카메라 거리는 학습된 scene의 해상도를 개선하는 데 도움이 된다고 한다.

2. Rendering

카메라 포즈와 광원 위치가 주어지면, 64$\times$64에서 shaded NeRF model을 렌더링한다. 조명이 있는 컬러 렌더링, 텍스처 없는 렌더링, shading이 없는 알베도 렌더링 중에서 랜덤하게 선택한다.

3. Diffusion loss with view-dependent conditioning

텍스트 프롬프트는 객체의 표준 view는 잘 설명하지만, 다른 view를 샘플링할 때는 좋은 설명이 아니다. 따라서 랜덤하게 샘플링된 카메라의 위치에 기반하여 view에 따라 다른 텍스트를 원래 텍스트에 추가하는 것이 유익하다. $\phi_\textrm{cam} > 60^\circ$의 경우 “overhead view”를 추가하고 $\phi_\textrm{cam} \le 60^\circ$의 경우 $\theta_\textrm{cam}$에 따라 “front view”, “side view”, “back view”를 추가하기 위해 텍스트 임베딩의 가중치 조합을 사용한다.

Imagen의 사전 학습된 64$\times$64 base text-to-image model을 사용한다. 이 모델은 대규모 웹 이미지-텍스트 데이터로 학습되었으며 T5-XXL 텍스트 임베딩에 의존한다. 저자들은 가중치 함수 $w(t) = \sigma_t^2$를 사용하였지만, 균일한 가중치를 사용하는 것도 유사한 결과를 보였다고 한다. 수치적 불안정성으로 인한 매우 높고 낮은 noise level을 피하기 위해 $t \sim \mathcal{U}(0.02, 0.98)$에서 샘플링한다. Classifier-free guidance의 경우, $\omega = 100$으로 설정하였으며, guidance 가중치가 높을수록 샘플 품질이 향상된다는 것을 알 수 있었다고 한다. 이는 이미지 샘플링 방법보다 훨씬 더 크며 작은 guidance 가중치에서 과도하게 oversmoothing되는 목적함수의 모드 탐색 특성으로 인해 필요할 수 있다. 렌더링된 이미지와 샘플링된 timestep $t$가 주어지면 노이즈를 샘플링하고 NeRF 파라미터의 기울기를 계산한다.

4. Optimization

본 논문의 3D scene은 칩이 4개인 TPUv4 시스템에 최적화되어 있다. 각 칩은 별도의 view를 렌더링하고 device당 batch size 1로 diffusion U-Net을 평가한다. 약 1.5시간이 걸리는 15,000 iteration으로 최적화한다. 컴퓨팅 시간은 NeRF 렌더링과 diffusion model 평가 사이의 균등하게 분할된다. 파라미터는 Distributed Shampoo optimizer를 사용하여 최적화돤다.

Experiments

다음 그림은 3D scene을 생성하고 정제하는 DreamFusion의 능력을 보여준다.

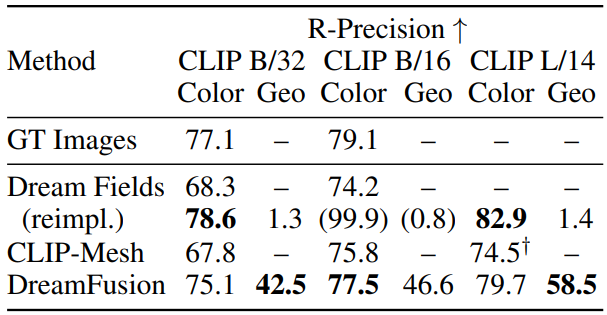
다음은 다양한 CLIP retrieval model로 생성한 캡션들로 DreamFusion의 생성의 일관성을 평가한 표이다.

다음은 baseline과의 정성적인 비교를 나타낸 것이다.

Ablations

다음은 DreamFusion의 ablation study 결과를 나타낸 표이다.

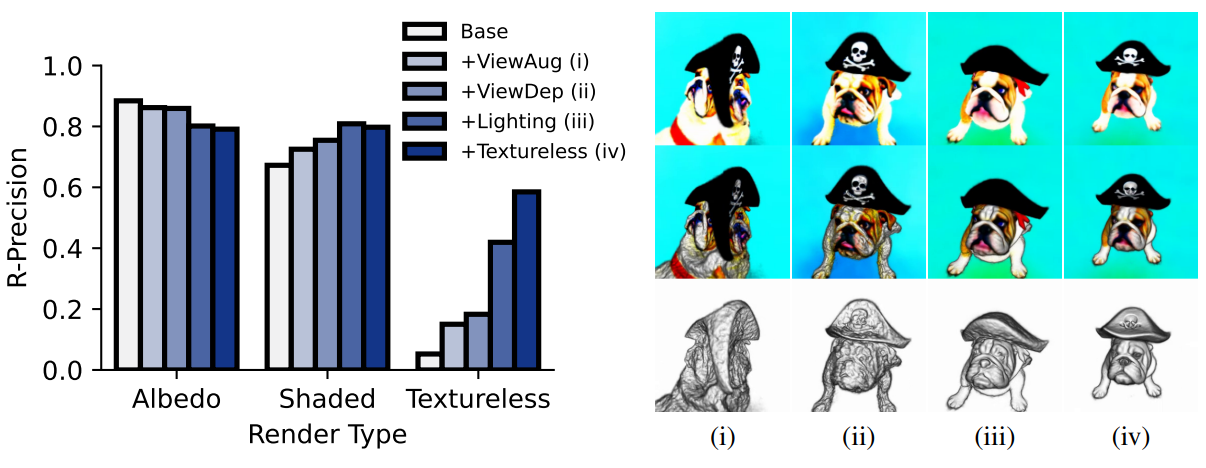
왼쪽은 object-centric COCO에서 CLIP L/14를 사용하여 다양한 render에 따른 빛이 없는 렌더링의 구성 요소를 평가한다. 오른쪽은 각 render의 효과를 “A bulldog is wearing a black pirate hat.”에 대하여 시각화한 것이다.